Event-triggered stabilizing controllers based on an exponentially decreasing threshold
May 24, 2017·
,
 ·
0 min read
·
0 min read
Fairouz Zobiri
Nacim Meslem
Brigitte Bidegaray-Fesquet
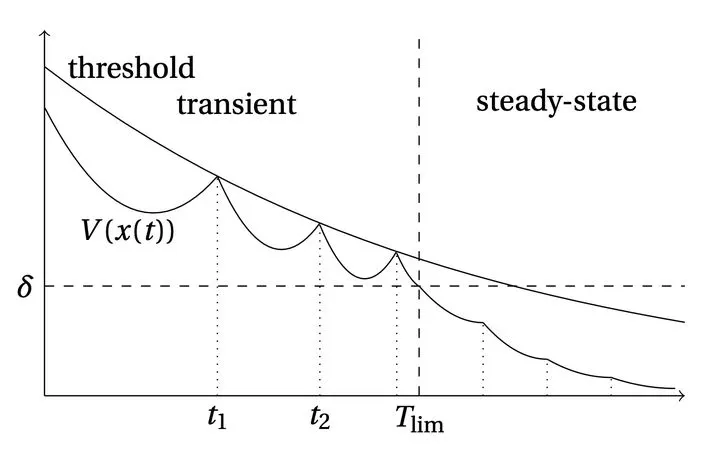 Transient and steady-state regimes
Transient and steady-state regimes
Abstract
In this paper, we introduce a new policy defining a stabilizing event-based controller for linear time-invariant systems. The plant operation is divided into two phases, a transient phase and a steady-state regime. In transient regime, we define a Lyapunov-like function; a positive definite function that vanishes only at the origin. However, while a regular Lyapunov function is decaying in time, the Lyapunov-like function is allowed to increase, provided that it remains bounded, in order to get larger inter-event times. An upper threshold is thus fixed in the form of an exponentially decaying function, the rate of decay of which is set by solving a generalized eigenvalue problem. In the vicinity of the steady state, the Lyapunov function is prevented from increasing in time to ensure a faster convergence with less control updates.
Type
Publication
EBCCSP 2017 - 3rd IEEE Conference on Event-Based Control Communication and Signal Processing, Funchal, Portugal (2017)