Non-uniform filter interpolation in the frequency domain
Interpolations of a Chebyshev filter in the complex plane
Abstract
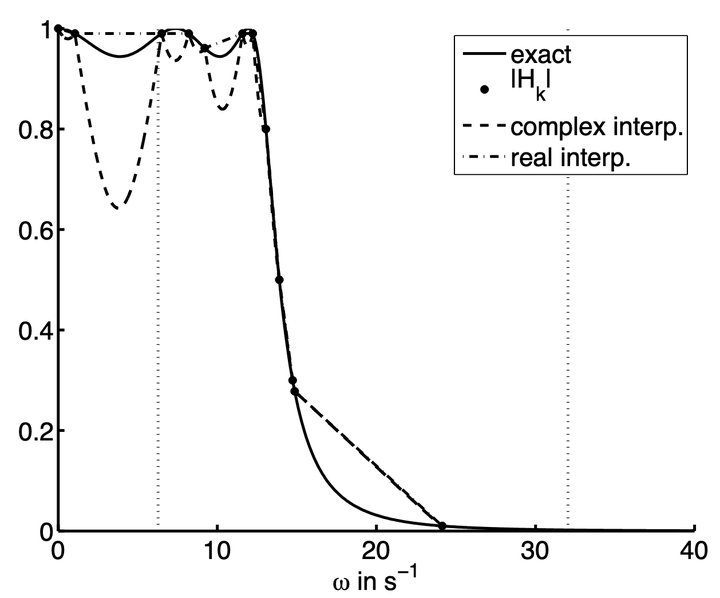
We propose a filtering technique which takes advantage of a specific non-uniform sampling scheme which allows the capture of a very low number of samples for both the signal and the filter transfer function. This approach leads to a summation formula which plays the same role as the discrete convolution for usual FIR filters. Here the formula is much more complicated but it can easily be implemented and the evaluation of these more elaborate expressions is compensated by the very low number of samples to process.
Type
Publication
Sampling Theory in Signal and Image Processing, 10, 17–35 (2011)
