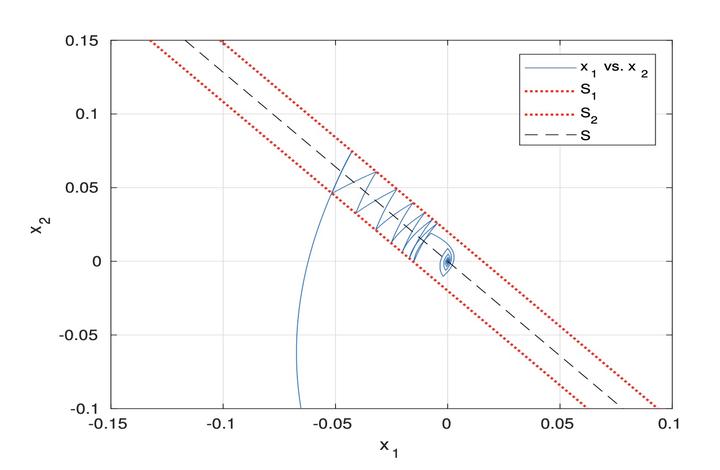
 Phase portrait
Phase portrait
Abstract
We introduce an event-triggered algorithm for the stabilization of switched linear systems. We define a pseudo-Lyapunov function common to all the subsystems. The pseudo-Lyapunov function is compared, at every time instant, to an exponentially decreasing upper threshold. An event is generated when the two functions intersect, or when a new subsystem becomes active. The existence of a Lyapunov function common to all the subsystems is a key requirement of this method. Nevertheless, imposing this condition does not add to the complexity of the problem. Indeed, we formulate the problem in terms of Linear Matrix Inequalities, as a generalized eigenvalue problem. This formulation allows to simultaneously check for the existence of a common Lyapunov function and to obtain the optimal parameters to define the upper threshold. We prove the stability of the system under the event-triggered control and we show that successive events are separated by a minimum interval of time.