this class is a test class for testing wave equation using the Finite elements Method with two implementation of the obtained mass matrix as diagonal or not. More...
#include <EMM_WaveFEMTest.h>
Public Member Functions | |
| void | setIsCondensedMassMatrix (const tBoolean &isCondensed) |
| set true if the Mass Matrix is condensed or not More... | |
| virtual tBoolean | test (const CORE_Run &runner, const map< tString, tString > &options) const |
| make the test More... | |
| virtual tBoolean | performanceTest (const CORE_Run &runner, const map< tString, tString > &options) const |
| make the perfomance tests More... | |
| tString | searchPath (const tString &fileName) const |
| set the path to find the file with name fileName More... | |
| void | getSearchingPaths (vector< tString > &vpaths) const |
| get the path fro seaching the files More... | |
| SP::EMM_Grid3D | createDomain (const tBoolean periodicity[3], const tReal L[3], const tUInteger N[3]) const |
| create a cubic mesh More... | |
| void | createMatters (EMM_MatterField &matters, const tUIndex &nMatters, const tFlag &anisotropy, const tUIndex &nCells, const tReal &Lmin, const tReal &Lmax) const |
| create matters & distribution on matters More... | |
| void | computeMField (const tString &path, EMM_RealField &M, const tReal &initSeed) const |
| compute normalized magnetization field More... | |
| void | computeMField (EMM_RealField &M, const tReal &initSeed) const |
| compute normalized magnetization field More... | |
| SP::EMM_LandauLifschitzSystem | createSystem (const CORE_Run &runner, const map< tString, tString > &options) const |
| create the system More... | |
| tBoolean | testType () const |
| test type More... | |
| void | getSharedPointer (SP::CORE_Object &p) |
| get the shared pointer of this class into p More... | |
| void | getSharedPointer (SPC::CORE_Object &p) const |
| get the shared pointer of this class into p More... | |
| tString | getClassName () const |
| return the class name of the object More... | |
| tString | getIdentityString () const |
| return the identity string of the object of the form className_at_address More... | |
| tString | getPointerAddress () const |
| return the identity string of the object More... | |
| template<class T > | |
| tBoolean | isInstanceOf () const |
| test if the clas T is an instance of this class More... | |
| tBoolean | isInstanceOf (const tString &name) const |
| test if the object is an instance of className More... | |
| virtual tString | toString () const |
| return the string representation of the object node More... | |
Static Public Member Functions | |
| static SP::EMM_WaveFEMTest | New () |
| create a test class More... | |
| static tReal | compareField (const EMM_RealField &F, const EMM_RealField &G, tUIndex &indexMax) |
| compare 2 fields More... | |
| static tBoolean | isInBox (const tReal dim[3], const tReal x[3]) |
| return true if x[k] is in the [0,dim[k]] for all k in [0,3[ More... | |
| static SP::EMM_Grid3D | createCube (const tReal dim[3], const tUInteger N[3]) |
| create a cube More... | |
| static SP::EMM_Grid3D | createBox (const tReal dim[3], const tUInteger N[3]) |
| create a box More... | |
| static void | setIsMemoryChecked (const tBoolean &v) |
| set if the memory checking is used More... | |
| static void | setOut (SP::CORE_Out out) |
| set the output stream More... | |
| static void | resetOut () |
| reset the output stream More... | |
| static void | setThread (SP::CORE_Thread thread) |
| set the thread More... | |
| static void | resetThread () |
| reset the output stream More... | |
| static CORE_Out & | out () |
| get the output More... | |
| static SP::CORE_Out | getOut () |
| get the output More... | |
| static CORE_Thread & | getThread () |
| get the profilier More... | |
| static const tBoolean & | isMemoryChecked () |
| get if the memory checking is used More... | |
| static tString | getClassName (const tString &identityString) |
| return the class name of the object More... | |
| template<class T > | |
| static tString | getTypeName () |
| get type name More... | |
| static tBoolean | is64Architecture () |
| return true if the machine is a 64 bits machine More... | |
| static tBoolean | is32Architecture () |
| return true if the machine is a 32 bits machine More... | |
| static tString | pointer2String (const void *obj) |
| return the string representation of a pointer More... | |
| static void | printObjectsInMemory (ostream &f) |
| print object in memory More... | |
| static void | printObjectsInMemory () |
| print object in memory in the standart output More... | |
| static tChar | getMaxChar () |
| get the max value for tChar type More... | |
| static tChar | getMinChar () |
| get the min value for tChar type More... | |
| static tUChar | getMaxUChar () |
| get the max value for tUChar type More... | |
| static tUChar | getMinUChar () |
| get the min value for tUChar type More... | |
| static tSInt | getMaxSInt () |
| get the max value for tSInt type More... | |
| static tSInt | getMinSInt () |
| get the min value for tSInt type More... | |
| static tUSInt | getMaxUSInt () |
| get the max value for tUSInt type More... | |
| static tUSInt | getMinUSInt () |
| get the min value for tUSInt type More... | |
| static tInt | getMaxInt () |
| get the max value for tInt type More... | |
| static tInt | getMinInt () |
| get the min value for tInt type More... | |
| static tUInt | getMaxUInt () |
| get the max value for tUInt type More... | |
| static tUInt | getMinUInt () |
| get the min value for tUInt type More... | |
| static tLInt | getMaxLInt () |
| get the max value for tLInt type More... | |
| static tLInt | getMinLInt () |
| get the min value for tLInt type More... | |
| static tULInt | getMaxULInt () |
| get the max value for tULInt type More... | |
| static tULInt | getMinULInt () |
| get the min value for tULInt type More... | |
| static tLLInt | getMaxLLInt () |
| get the max value for tULInt type More... | |
| static tLLInt | getMinLLInt () |
| get the min value for tLLInt type More... | |
| static tULLInt | getMaxULLInt () |
| get the max value for tULLInt type More... | |
| static tULLInt | getMinULLInt () |
| get the min value for tULLInt type More... | |
| static tFloat | getMaxFloat () |
| get the max value for tFloat type More... | |
| static tFloat | getMinFloat () |
| get the min value for tFloat type More... | |
| template<class T > | |
| static T | getEpsilon () |
| get the epsilon value for T type More... | |
| template<class T > | |
| static T | getInfinity () |
| get the infinity for T type More... | |
| static tFloat | getFloatEpsilon () |
| get the epsilon value for tFloat type More... | |
| static tFloat | getFloatInfinity () |
| get the infinity value for tFloat type More... | |
| static tDouble | getMaxDouble () |
| get the max value for tDouble type More... | |
| static tDouble | getMinDouble () |
| get the min value for tDouble type More... | |
| static tDouble | getDoubleInfinity () |
| get the infinity value for tFloat type More... | |
| static tDouble | getDoubleEpsilon () |
| get the epsilon value for tDouble type More... | |
| static tLDouble | getMinLDouble () |
| get the min value for tLDouble type More... | |
| static tLDouble | getMaxLDouble () |
| get the max value for tLDouble type More... | |
| static tLDouble | getLDoubleEpsilon () |
| get the epsilon value for tLDouble type More... | |
| static tDouble | getLDoubleInfinity () |
| get the infinity value for tDouble type More... | |
| static tIndex | getMaxIndex () |
| get the max value for the array/vector indexing type More... | |
| static tIndex | getMinIndex () |
| get the min value for the array/vector indexing type More... | |
| static tUIndex | getMaxUIndex () |
| get the max value for difference the array/vector indexing type More... | |
| static tUIndex | getMinUIndex () |
| get the min value for difference the array/vector indexing type More... | |
| static tFlag | getMaxFlag () |
| get the max value for the tFlag type More... | |
| static tFlag | getMinFlag () |
| get the min value for the tFlag type More... | |
| static tUInteger | getMaxUInteger () |
| get the max value for the unsigned integer type More... | |
| static tUInteger | getMinUInteger () |
| get the min value for the unsigned integer type More... | |
| static tInteger | getMaxInteger () |
| get the max value for the integer type More... | |
| static tInteger | getMinInteger () |
| get the min value for the integer type More... | |
| static tReal | getMaxReal () |
| get the max value for the real type More... | |
| static tReal | getMinReal () |
| get the min value for the real type More... | |
| static tReal | getRealEpsilon () |
| get the eps which is the difference between 1 and the least value greater than 1 that is representable. More... | |
| static tReal | getRealInfinity () |
| get the infinity value More... | |
| template<class T > | |
| static T | computeEpsilon () |
| compute epsilon More... | |
Static Public Attributes | |
| static const tFlag | PRIMARY_TESTS =0 |
| static const tFlag | ELEMENTARY_TESTS =1 |
| static const tFlag | CASE_TESTS =2 |
| static const tFlag | CASE_TEST =4 |
| static const tFlag | ALL_TESTS =3 |
Protected Member Functions | |
| EMM_WaveFEMTest (void) | |
| create the class More... | |
| virtual | ~EMM_WaveFEMTest (void) |
| destroy the class More... | |
| tBoolean | waveTE2Propagation (const tBoolean &isForward, const tBoolean &isTXTOutput, const tString &prefix, const tBoolean &isPeriodic, const tBoolean dirichletLC[2], tReal U_0(const tReal &t), tReal U_L(const tReal &t), const tReal &C, const tReal &L, const tReal &cfl, const tUIndex nT, EMM_RealArray &U, EMM_RealArray &V) const |
compute the wave at any time from initial conditions U(0,.) and V(0,x) and from dirichlet limit conditions 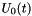 or/and or/and 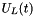 and/or Neumann limit conditions and/or Neumann limit conditions 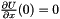 or/and or/and 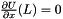 based on Taylor expansion of order 2 for time: based on Taylor expansion of order 2 for time: 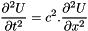 More... More... | |
| virtual tBoolean | waveSystemP1Propagation (const tBoolean &isTXTOutput, const tString &prefix, const tBoolean dirichletLC[2], tReal U_0(const tReal &t), tReal U_L(const tReal &t), const tReal &c, const tReal &L, const tReal &dt, const tUIndex nT, EMM_RealArray &U, EMM_RealArray &V) const |
compute the wave at any time from initial conditions U(0,.) and V(0,x) and from dirichlet limit conditions 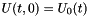 or/and or/and 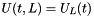 and/or Neumann limit conditions and/or Neumann limit conditions 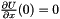 or/and or/and 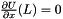 based on solving a system (U,V) : More... based on solving a system (U,V) : More... | |
| virtual tBoolean | waveSystemP2Propagation (const tBoolean &isTXTOutput, const tString &prefix, const tBoolean dirichletLC[2], tReal U_0(const tReal &t), tReal U_L(const tReal &t), const tReal &c, const tReal &L, const tReal &cfl, const tUIndex nT, EMM_RealArray &U, EMM_RealArray &V) const |
compute the wave at any time from initial conditions U(0,.) and V(0,x) and from dirichlet limit conditions 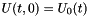 or/and or/and 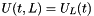 and/or Neumann limit conditions and/or Neumann limit conditions 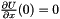 or/and or/and 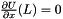 based on solving a system (V,W) More... based on solving a system (V,W) More... | |
| virtual tBoolean | sinusoidalWave () const |
| virtual tBoolean | triangleWave () const |
| virtual tBoolean | trianglePeriodicalWave () const |
| virtual tBoolean | sharkWave () const |
| virtual tBoolean | barWave () const |
| tReal | computeEnergy (const tUIndex &n, const tReal &C, const tReal &dx, const tReal &dt, const tReal *U, const tReal *Ut) const |
compute the energy of the wave : 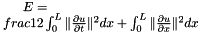 More... More... | |
| tBoolean | save (const tString &fileName, const tReal &dx, const tReal *U, const tUIndex &nPts) const |
| save the displacement at time with space space of dx More... | |
| tBoolean | save (const tString &fileName, const tReal &dx, const tReal *U, const tReal *V, const tUIndex &nPts) const |
| save the displacement at time with space space of dx More... | |
| tBoolean | load (const tString &optionFile, tString &path, tBoolean &isTXTOutput, tBoolean &isPeriodic, tBoolean dirichletLC[2], tReal &L, tUIndex &nPoints, tReal &Umax, tReal &C, tUIndex &nTimes, tReal &cfl) const |
| load the data from txt file More... | |
| tBoolean | sinusoidalWave (const tString &method) const |
| tBoolean | triangleWave (const tString &method) const |
| tBoolean | trianglePeriodicalWave (const tString &method) const |
| tBoolean | sharkWave (const tString &method) const |
| tBoolean | barWave (const tString &method) const |
| void | setThis (SP::CORE_Object p) |
| set this weak shared pointer called toDoAfterThis setting method More... | |
| virtual void | toDoAfterThisSetting () |
| method called after setThis() method this method can oly be called once. More... | |
Static Protected Member Functions | |
| static tReal | null_function (const tReal &t) |
| static tReal | shark_function (const tReal &t) |
| static tReal | triangle_function (const tReal &L, const tReal &U, const tReal &x) |
| static tReal | sinusoidal_function (const tReal &L, const tReal &U, const tReal &x) |
| static void | linearPieceWise_function (const tUInteger &n, const tReal *X, const tReal *Y, const tUInteger &nEvals, const tReal *Xvalues, tReal *Yvalues) |
Private Member Functions | |
| SP_OBJECT (EMM_WaveFEMTest) | |
| void | computeMassMatrix (const tUIndex &nPts, const tBoolean &isPeriodic, const tBoolean dirichletLC[2], MATH_FullMatrix &M) const |
| compute the mass matrix More... | |
| void | computeCondensedMassMatrix (const tUIndex &nPts, const tBoolean &isPeriodic, const tBoolean dirichletLC[2], MATH_ArrayVector &M) const |
| compute the condensed mass matrix as diagonal More... | |
| void | computeStressMatrix (const tUIndex &nPts, const tBoolean &isPeriodic, const tBoolean dirichletLC[2], MATH_FullMatrix &S) const |
| compute the stress matrix More... | |
| tBoolean | computeWaveAtFirstTime (const MATH_Matrix &M, const MATH_Matrix &X, MATH_Solver &solver, const tBoolean &isPeriodic, const tBoolean dirichletLC[2], tReal U0(const tReal &t), tReal UL(const tReal &t), EMM_RealArray &Ux_0, EMM_RealArray &dU_dt0, const tReal &s, const tReal &dt, EMM_RealArray &Ux_1) const |
| compute the wave U(dt,.) with Dirichlet/Neumann limit conditions More... | |
| tBoolean | computeWaveAtFirstTime (const MATH_ArrayVector &M, const MATH_Matrix &X, const tBoolean &isPeriodic, const tBoolean dirichletLC[2], tReal U0(const tReal &t), tReal UL(const tReal &t), EMM_RealArray &Ux_0, EMM_RealArray &dU_dt0, const tReal &s, const tReal &dt, EMM_RealArray &Ux_1) const |
| compute the wave U(dt,.) with Dirichlet/Neumann limit conditions More... | |
Private Attributes | |
| tBoolean | mIsMassMatrixCondensed |
Detailed Description
this class is a test class for testing wave equation using the Finite elements Method with two implementation of the obtained mass matrix as diagonal or not.
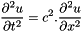
The aproximation of time is either
- Taylor Expansion of order 2 :
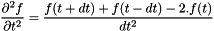 and
and 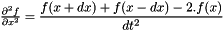 (see EMM_WaveFEMTest::waveTE2Propagation() )
(see EMM_WaveFEMTest::waveTE2Propagation() ) - a system or order 1 with 2 variables : displacement and velocity (see EMM_WaveFEMTest::waveSystemP1Propagation() not yet implemented).
a system of order 1 with 2 varaibles : velocity and deformation (see EMM_WaveFEMTest::waveSystemP2Propagation() not yet implemented).
- Version
- 1.0
Constructor & Destructor Documentation
◆ EMM_WaveFEMTest()
|
protected |
create the class
References mIsMassMatrixCondensed.
Referenced by New().

◆ ~EMM_WaveFEMTest()
|
protectedvirtual |
destroy the class
Member Function Documentation
◆ barWave() [1/2]
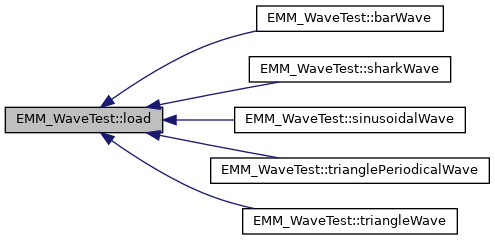
References EMM_Test::caseTest(), CORE_Array< T >::initArray(), EMM_WaveTest::linearPieceWise_function(), EMM_WaveTest::load(), EMM_WaveTest::null_function(), CORE_Array< T >::setSize(), tBoolean, tReal, tString, tUIndex, tUInteger, tUSInt, EMM_WaveTest::waveSystemP1Propagation(), EMM_WaveTest::waveSystemP2Propagation(), and EMM_WaveTest::waveTE2Propagation().
◆ barWave() [2/2]
|
inlineprotectedvirtual |
Implements EMM_WaveTest.
References EMM_WaveTest::barWave().

◆ compareField()
|
staticinherited |
compare 2 fields
- Parameters
-
F the field to compare G the secund field to compare indexMax the index where the diffrenec of the norm is maximum
- Returns
- the max norm difference among all points
References EMM_RealField::getDimension(), EMM_RealField::getSize(), EMM_RealField::getValue(), tBoolean, tDimension, tReal, and tUIndex.
Referenced by EMM_Test::New(), and EMM_ODETest::testODE().


◆ computeCondensedMassMatrix()
|
private |
compute the condensed mass matrix as diagonal
- Parameters
-
nPts number of rows/columns of the mass matrix isPeriodic to set if the matrix is supposed to be periodic dirichletLC : limite conditions M the mass matrix
The mass matrix corresponding to the approximation of the integration of 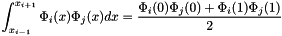 where
where 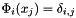 is a basis function P1 interpolation is as follow:
is a basis function P1 interpolation is as follow:
![$ M = \left[ {\begin{array}{cccccc} \frac{1}{2} & 0 & ... & 0 & 0 & 0 \\ 0 & 1 & 0 & ... & 0 & 0 \\ 0 & 0 & 1 & 0 && ... \\ ... & ... & ... & ...& ... & ... \\ 0 & 0 & ...& 0 & 1 & 0 \\ 0& ... & 0 & 0 & 1 & \frac{1}{2} \end{array} } \right] $](form_1348.png)
If the condition is dirichlet at point 0 then 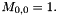 or/and at point L then
or/and at point L then 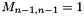 and 0 on other columns.
and 0 on other columns.
References MATH_ArrayVector::setSize(), tReal, and tUIndex.
Referenced by setIsCondensedMassMatrix(), and waveTE2Propagation().


◆ computeEnergy()
|
protectedinherited |
compute the energy of the wave : 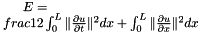
- Parameters
-
n : number of point C celerity of the wave dx space step size dt time step size U : U at t Ut U at t+dt
References null, tReal, and tUIndex.
Referenced by EMM_WaveFDMTest::waveSystemP2Propagation(), EMM_WaveFDMTest::waveTE2Propagation(), and waveTE2Propagation().

◆ computeEpsilon()
|
inlinestaticinherited |
compute epsilon
- Returns
- the epsilon value eps=10^{-p/3} where p is defined by getEpsilon()=10^{-p}
◆ computeMassMatrix()
|
private |
compute the mass matrix
- Parameters
-
nPts number of rows/columns of the mass matrix isPeriodic to set if the matrix is supposed to be periodic dirichletLC : limite conditions M the mass matrix
The mass matrix corresponding to the exact integration of 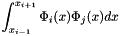 where
where 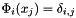 is a basis function P1 interpolation is as follow:
is a basis function P1 interpolation is as follow:
![$ M = \left[ {\begin{array}{cccccc} \frac{1}{3} & \frac{1}{6} & ... & 0 & 0 & 0 \\ \frac{1}{6} & \frac{2}{3} & \frac{1}{6} & ... & 0 & 0 \\ 0 & \frac{1}{6} & \frac{2}{3} & \frac{1}{6} && ... \\ ... & ... & ... & ...& ... & ... \\ 0 & 0 & ...& \frac{1}{6} & \frac{2}{3} & \frac{1}{6} \\ 0& ... & 0 & 0 & \frac{1}{6} & \frac{1}{3} \end{array} } \right] $](form_1344.png)
If the condition is dirichlet at point 0 then 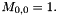 or/and at point L then
or/and at point L then 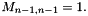 , and 0 on other columns.
, and 0 on other columns.
References MATH_FullMatrix::setSize(), MATH_FullMatrix::setValues(), tReal, and tUIndex.
Referenced by setIsCondensedMassMatrix(), and waveTE2Propagation().


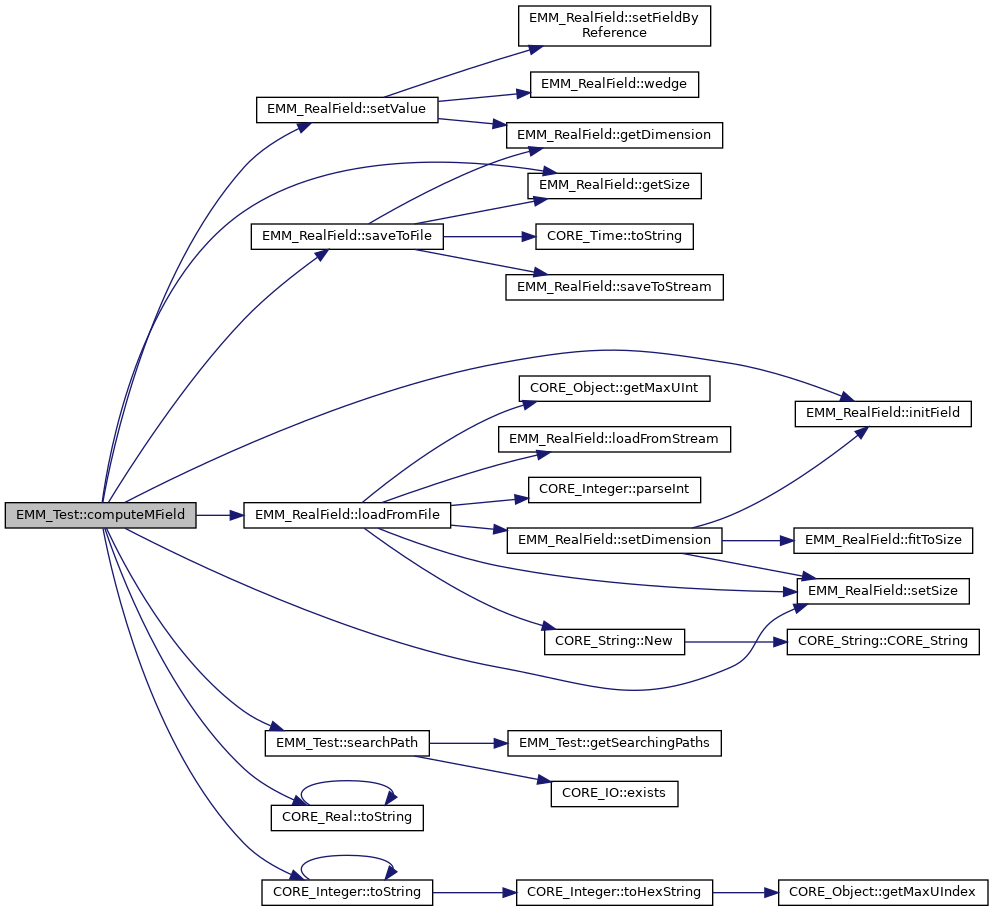
◆ computeMField() [1/2]
|
inherited |
compute normalized magnetization field
- Parameters
-
[in] path : path to find the M file if any [out] M : field to generate [in] initSeed : type of initialization of the fields : - -1 : M=(1,0,0)
- -2 : M=(0,1,0)
- -3 : M=(0,0,1)
- -4 : M=(1,1,1)
- -5 : M=(0,1,1)
- -6 : M=(1,1,0)
- -7 : M=(1,0,1)
- >=0 : it loads the file M_nCells_initSeed.txt it its exists or create a random M and try to generete in in the path whre the file is supposed to be. The field M must be sized before.
References EMM_RealField::getSize(), EMM_RealField::initField(), EMM_RealField::loadFromFile(), EMM_RealField::saveToFile(), EMM_Test::searchPath(), EMM_RealField::setSize(), EMM_RealField::setValue(), tBoolean, CORE_Real::toString(), CORE_Integer::toString(), tReal, tString, and tUIndex.
Referenced by EMM_Test::computeMField(), and EMM_Test::New().

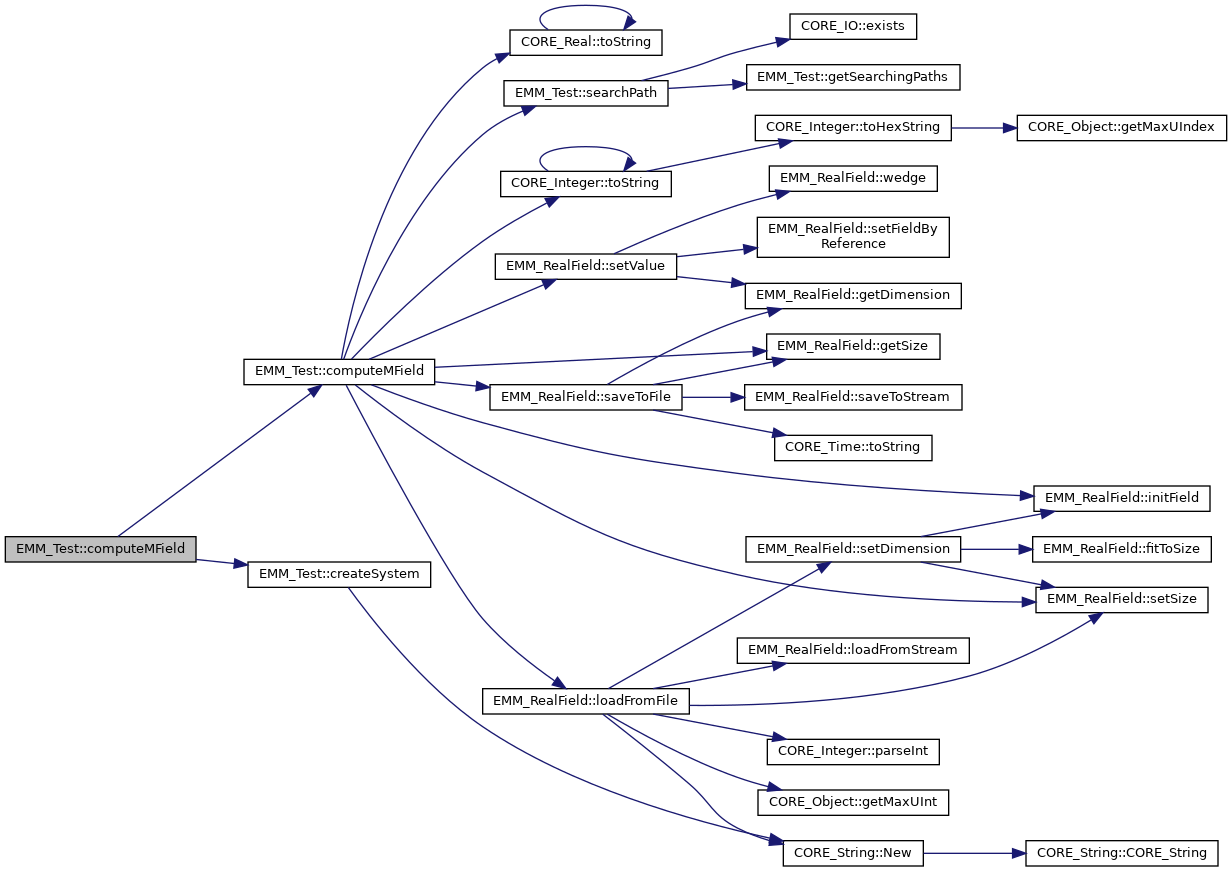
◆ computeMField() [2/2]
|
inlineinherited |
compute normalized magnetization field
- Parameters
-
[out] M : field to generate [in] initSeed : type of initialization of the fields : - -1 : M=(1,0,0)
- -2 : M=(0,1,0)
- -3 : M=(0,0,1)
- -4 : M=(1,1,1)
- -5 : M=(0,1,1)
- -6 : M=(1,1,0)
- -7 : M=(1,0,1)
- >=0 : it loads the file M_nCells_initSeed.txt it its exists or create a random M and try to generete in in the path whre the file is supposed to be. The field M must be sized before.
References EMM_Test::computeMField(), and EMM_Test::createSystem().
◆ computeStressMatrix()
|
private |
compute the stress matrix
- Parameters
-
nPts number of rows/columns of the mass matrix isPeriodic to set if the stress is supposed to be periodic dirichletLC : limite conditions S the stress matrix
The stress matrix corresponding to the exact integration of 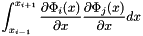 where
where 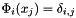 is a basis function P1 interpolation is as follow:
is a basis function P1 interpolation is as follow:
![$ S = \left[ {\begin{array}{cccccc} 1 & -1 & ... & 0 & 0 & 0 \\ -1 & 2 & -1 & ... & 0 & 0 \\ 0 & -1 & 2 & -1 && ... \\ ... & ... & ... & ...& ... & ... \\ 0 & 0 & ...& -1 & 2 & -1 \\ 0& ... & 0 & 0 & -1 & 1 \end{array} } \right] $](form_1351.png)
References MATH_FullMatrix::setSize(), MATH_FullMatrix::setValues(), tReal, and tUIndex.
Referenced by setIsCondensedMassMatrix(), and waveTE2Propagation().


◆ computeWaveAtFirstTime() [1/2]
|
private |
compute the wave U(dt,.) with Dirichlet/Neumann limit conditions
- Parameters
-
M : mass matrix X : displacement matrix solver : linear solver isPeriodic to set if the wave is supposed to be periodic dirichletLC limit condition of dirichlet U0 : function depending on time t at x=0 if dirichlet condition UL : function depending on time t at x=L if dirichlet condition Ux_0 : initial value of U at t=0 for all x in [0,L[ dU_dt0 : initial value of velocity of U at t=0 for all x in [0,L[ s the quantity 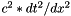
dt : the time step Ux_1 : return the values of U at t=dt
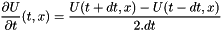
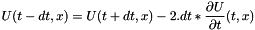
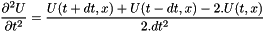
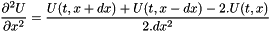
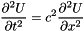
By multipliing by a basis function 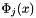 and integration over the domain, we obtain the ssystem equation:
and integration over the domain, we obtain the ssystem equation:
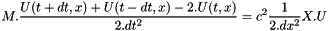
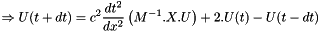
so we deduce at first step that :
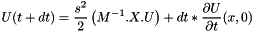 with
with 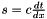
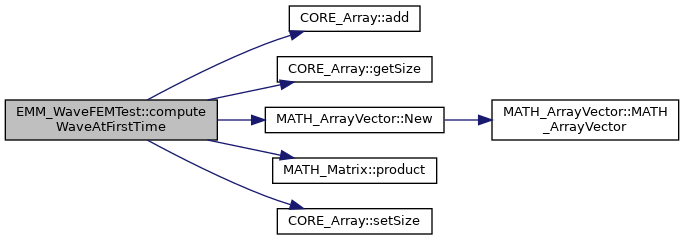
References CORE_Array< T >::add(), CORE_Array< T >::getSize(), MATH_ArrayVector::New(), MATH_Matrix::product(), CORE_Array< T >::setSize(), MATH_Solver::solve(), tReal, and tUIndex.
Referenced by setIsCondensedMassMatrix(), and waveTE2Propagation().
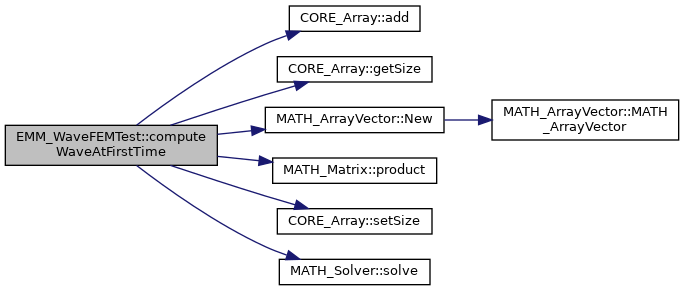

◆ computeWaveAtFirstTime() [2/2]
|
private |
compute the wave U(dt,.) with Dirichlet/Neumann limit conditions
- Parameters
-
M : condensed mass diagonal matrix X displacement matrix isPeriodic to set if the wave is supposed to be periodic dirichletLC limit condition of dirichlet U0 : function depending on time t at x=0 if dirichlet condition UL : function depending on time t at x=L if dirichlet condition Ux_0 : initial value of U at t=0 for all x in [0,L[ dU_dt0 : initial value of velocity of U at t=0 for all x in [0,L[ s the quantity 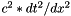
dt : the time step Ux_1 : return the values of U at t=dt
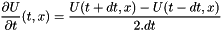
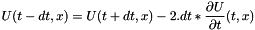
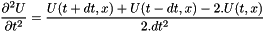
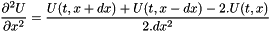
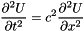
By multipliing by a basis function 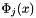 and integration over the domain, we obtain the ssystem equation:
and integration over the domain, we obtain the ssystem equation:
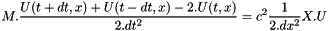
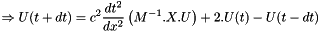
so we deduce at first step that :
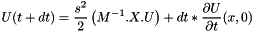 with
with 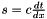
References CORE_Array< T >::add(), CORE_Array< T >::getSize(), MATH_ArrayVector::New(), MATH_Matrix::product(), CORE_Array< T >::setSize(), tReal, and tUIndex.
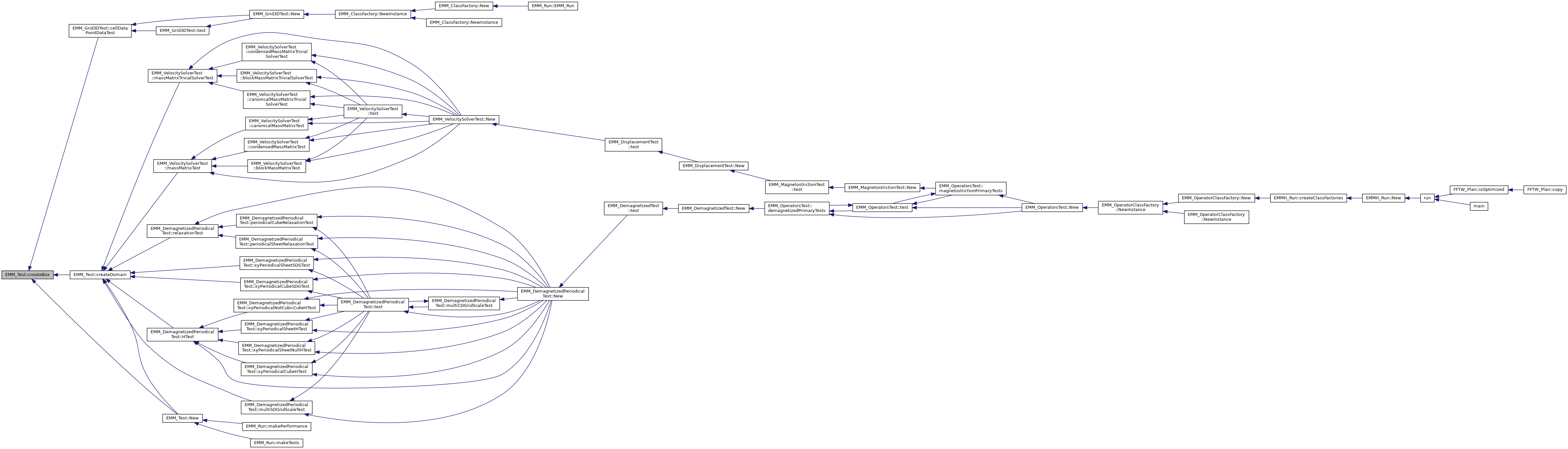
◆ createBox()
create a box
- Parameters
-
dim dimension of a parallelipiped box in each direction N number of discretization on each direction of the box
- Returns
- a share pointer to the grid 3D
References EMM_Grid3D::getNeighborsIndicators(), EMM_Test::isInBox(), EMM_Grid3D::New(), EMM_Grid3D::setSegmentsNumber(), EMM_Grid3D::setStepsSize(), tCellFlag, tReal, tUIndex, tUSInt, and EMM_Grid3D::updateMagnetizedElementsNumber().
Referenced by EMM_Grid3DTest::cellDataPointDataTest(), EMM_Test::createDomain(), and EMM_Test::New().

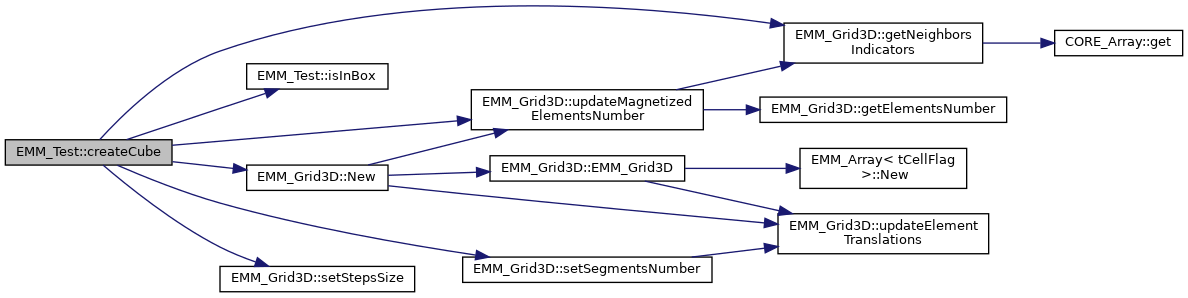
◆ createCube()
create a cube
- Parameters
-
dim dimension of a parallelipiped cube in each direction N number of discretization on each direction of the cube
- Returns
- a share pointer to the grid 3D
References EMM_Grid3D::getNeighborsIndicators(), EMM_Test::isInBox(), EMM_Grid3D::New(), EMM_Grid3D::setSegmentsNumber(), EMM_Grid3D::setStepsSize(), tCellFlag, tReal, tUInteger, tUSInt, and EMM_Grid3D::updateMagnetizedElementsNumber().
Referenced by EMM_Test::New(), EMM_TimeTest::testCubicAnisotropyEnergyDerivatives(), EMM_Grid3DTest::testSegment(), EMM_Grid3DTest::testThinSheet(), EMM_TimeTest::testTimeStepComputing(), and EMM_TimeTest::testZeemanEnergyDerivatives().

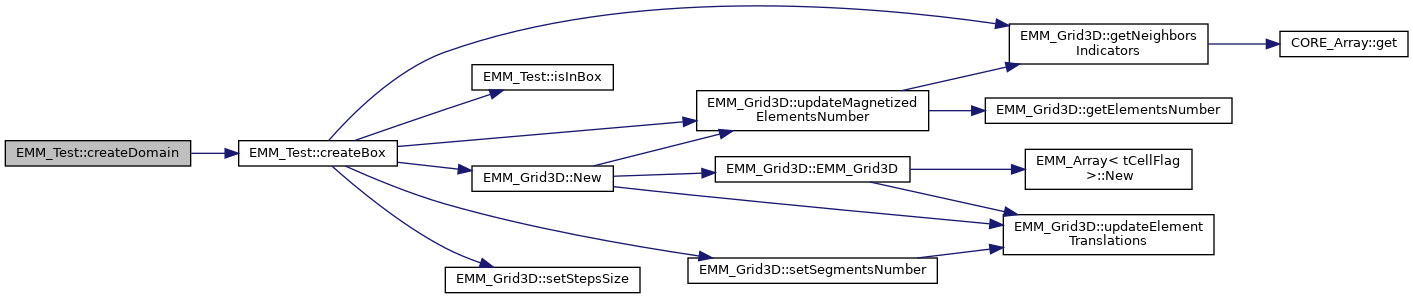
◆ createDomain()
|
inherited |
create a cubic mesh
- Parameters
-
[in] periodicity : periodicity of the domain [in] L : size of the domain [in] N : discretization of the domain
References EMM_Test::createBox().
Referenced by EMM_DemagnetizedPeriodicalTest::HTest(), EMM_VelocitySolverTest::massMatrixTest(), EMM_VelocitySolverTest::massMatrixTrivialSolverTest(), EMM_DemagnetizedPeriodicalTest::multiSDGridScaleTest(), EMM_Test::New(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().
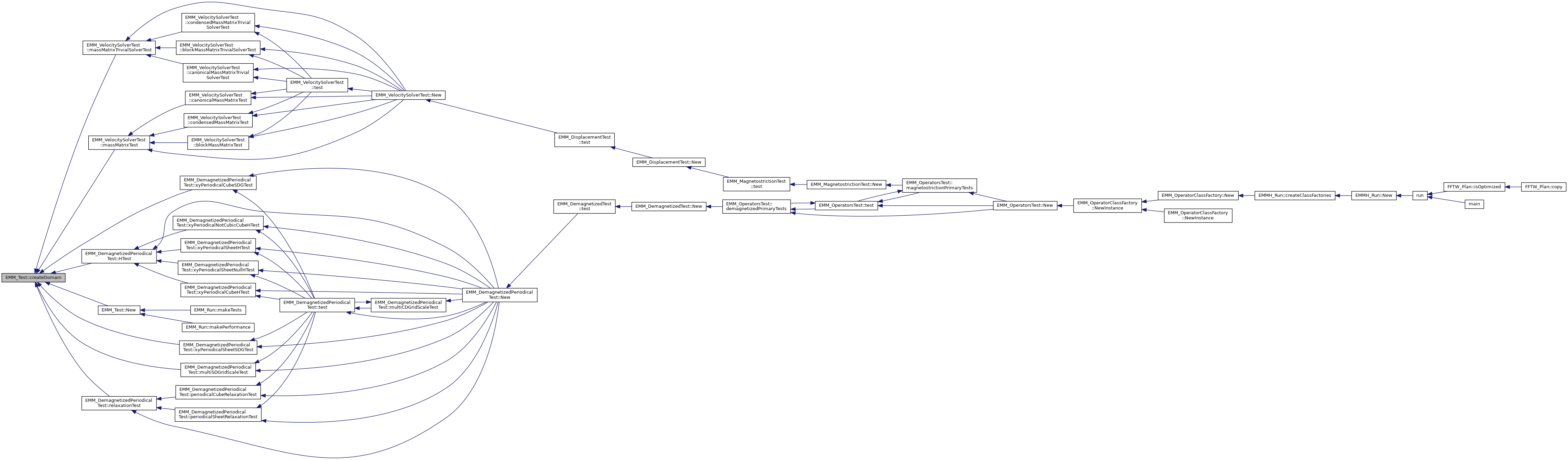
◆ createMatters()
|
inherited |
create matters & distribution on matters
- Parameters
-
[out] matters : matter field within the domain [in] nMatters : number of matters to generate [in] anisotropy : anisotrpy type of the matters [in] nCells : number of cells of the mesh [in] Lmin : min length of cells of the domain [in] Lmax : max length of cells of the domain
References EMM_MatterField::addMatter(), EMM_MatterField::adimensionize(), EMM_MatterField::clear(), EMM_Matter::CUBIC_ANISOTROPY, EMM_Object::Gamma, EMM_Object::Mu0, EMM_Matter::New(), EMM_Matter::PLANAR_ANISOTROPY, EMM_MatterField::setSize(), tReal, tUIndex, and tUSInt.
Referenced by EMM_DemagnetizedPeriodicalTest::HTest(), EMM_DemagnetizedPeriodicalTest::multiSDGridScaleTest(), EMM_Test::New(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().
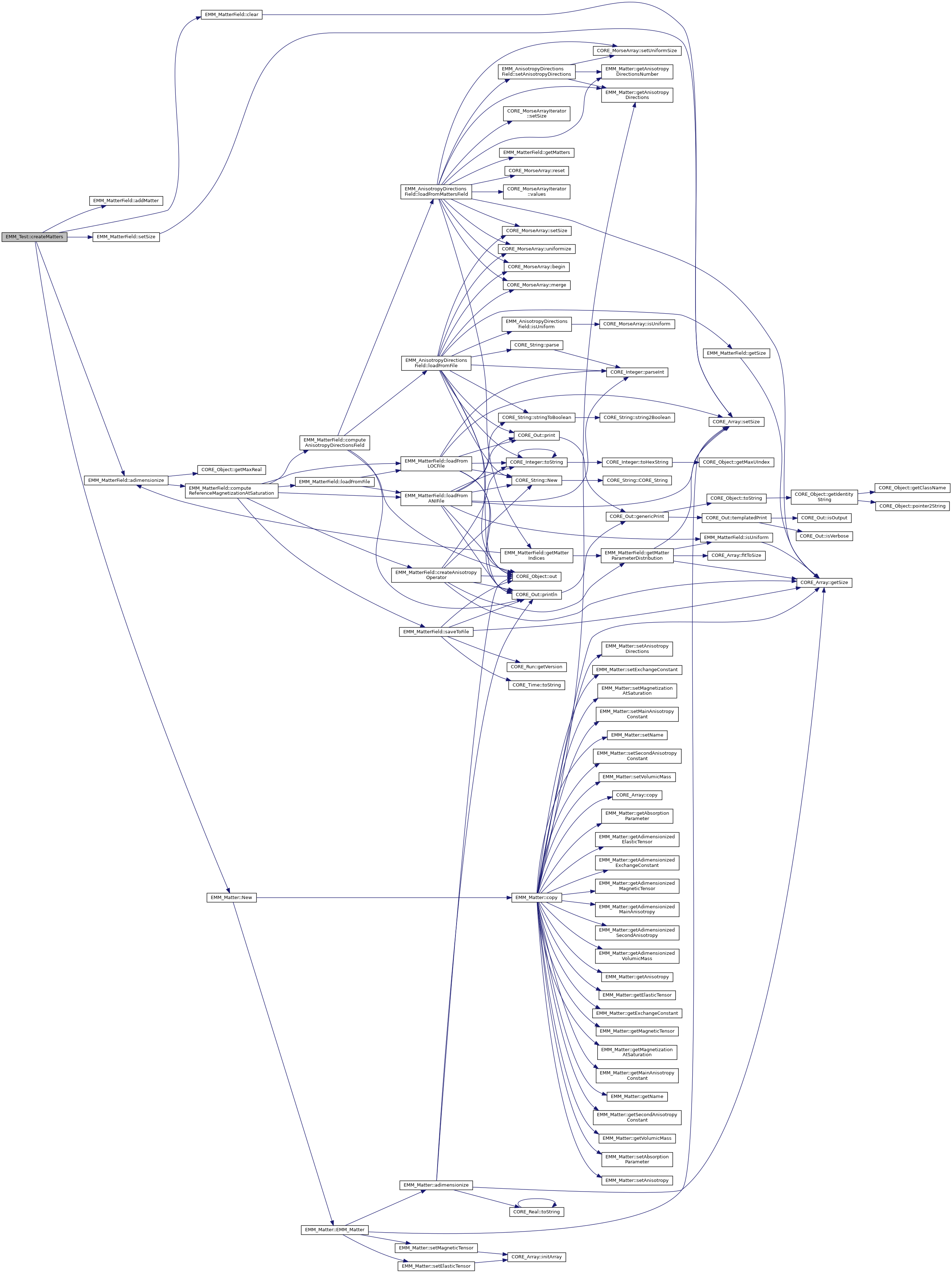

◆ createSystem()
|
inherited |
create the system
- Parameters
-
[in] runner : runner of the program to get the class factory [in] options : options to create the system - "relaxation-time-integration" = "gl"|"ggl"|"rk4"|"te"
- "relaxation-time order"="2"|"1"
- "relaxation-rate"="1.e-8"
- Returns
- the laudau lifschitz system
References CORE_String::New(), and tString.
Referenced by EMM_Test::computeMField(), EMM_DemagnetizedPeriodicalTest::HTest(), EMM_DemagnetizedPeriodicalTest::multiSDGridScaleTest(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().


◆ getClassName() [1/2]
|
inherited |
return the class name of the object
- Returns
- the class name of the object
References tString.
Referenced by CORE_Object::getIdentityString(), EMM_Operator::getName(), and CORE_Object::isMemoryChecked().

◆ getClassName() [2/2]
return the class name of the object
- Parameters
-
identityString the identity string of the object
- Returns
- the class name
◆ getDoubleEpsilon()
|
inlinestaticinherited |
get the epsilon value for tDouble type
- Returns
- the epsilon value for tDouble type
Referenced by CORE_Test::testType().
◆ getDoubleInfinity()
|
inlinestaticinherited |
get the infinity value for tFloat type
- Returns
- the intinity value for tFloat type
◆ getEpsilon()
|
inlinestaticinherited |
get the epsilon value for T type
- Returns
- the epsilon value for T type
◆ getFloatEpsilon()
|
inlinestaticinherited |
get the epsilon value for tFloat type
- Returns
- the epsilon value for tFloat type
Referenced by CORE_Test::testType().
◆ getFloatInfinity()
|
inlinestaticinherited |
get the infinity value for tFloat type
- Returns
- the intinity value for tFloat type
◆ getIdentityString()
|
inlineinherited |
return the identity string of the object of the form className_at_address
- Returns
- the identity string of the object
References CORE_Object::getClassName(), CORE_Object::pointer2String(), and tString.
Referenced by MATH_GaussLegendreIntegration::copy(), EMM_MultiScaleGrid::initialize(), CORE_Object::isInstanceOf(), CORE_Object::printObjectsInMemory(), MATH_Matrix::toString(), EMMG_SLPeriodicMultiScale::toString(), EMM_Stepper::toString(), EMM_AnisotropyDirectionsField::toString(), EMM_BlockMassMatrix::toString(), CORE_Object::toString(), EMM_Tensors::toString(), EMM_MultiScaleGrid::toString(), EMM_MatterField::toString(), EMM_Grid3D::toString(), and EMM_LandauLifschitzSystem::toString().

◆ getInfinity()
|
inlinestaticinherited |
get the infinity for T type
- Returns
- the infinity value for T type
◆ getLDoubleEpsilon()
|
inlinestaticinherited |
get the epsilon value for tLDouble type
- Returns
- the epsilon value for tLDouble type
Referenced by CORE_Test::testType().

◆ getLDoubleInfinity()
|
inlinestaticinherited |
get the infinity value for tDouble type
- Returns
- the infinity value for tDouble type
◆ getMaxChar()
|
inlinestaticinherited |
get the max value for tChar type
- Returns
- the max value for tChar type
Referenced by CORE_Test::testType().

◆ getMaxDouble()
|
inlinestaticinherited |
get the max value for tDouble type
- Returns
- the max value for tDouble type
Referenced by CORE_Test::testType().
◆ getMaxFlag()
|
inlinestaticinherited |
get the max value for the tFlag type
- Returns
- the max value for the tFlag type
Referenced by CORE_Test::testType().

◆ getMaxFloat()
|
inlinestaticinherited |
get the max value for tFloat type
- Returns
- the max value for tFloat type
Referenced by CORE_Test::testType().
◆ getMaxIndex()
|
inlinestaticinherited |
get the max value for the array/vector indexing type
- Returns
- the max value for the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMaxInt()
|
inlinestaticinherited |
get the max value for tInt type
- Returns
- the max value for tInt type
Referenced by MATSGN_FFT::fastFourierTransform3D_FFTW(), and CORE_Test::testType().

◆ getMaxInteger()
|
inlinestaticinherited |
get the max value for the integer type
- Returns
- the max value for the integer type
Referenced by CORE_Test::testType().
◆ getMaxLDouble()
|
inlinestaticinherited |
get the max value for tLDouble type
- Returns
- the max value for tLDouble type
Referenced by CORE_Test::testType().
◆ getMaxLInt()
|
inlinestaticinherited |
get the max value for tLInt type
- Returns
- the max value for tLInt type
Referenced by CORE_Test::testType().

◆ getMaxLLInt()
|
inlinestaticinherited |
get the max value for tULInt type
- Returns
- the max value for tULInt type
Referenced by CORE_Test::testType().
◆ getMaxReal()
|
inlinestaticinherited |
get the max value for the real type
- Returns
- he max value for the real type
Referenced by EMM_MatterField::adimensionize(), and CORE_Test::testType().

◆ getMaxSInt()
|
inlinestaticinherited |
get the max value for tSInt type
- Returns
- the max value for tSInt type
Referenced by CORE_Test::testType().
◆ getMaxUChar()
|
inlinestaticinherited |
get the max value for tUChar type
- Returns
- the max value for tUChar type
Referenced by CORE_Test::testType().
◆ getMaxUIndex()
|
inlinestaticinherited |
get the max value for difference the array/vector indexing type
- Returns
- the max value for difference the array/vector indexing type
Referenced by CORE_Vector< T >::addAfterIndices(), CORE_Vector< T >::search(), CORE_Test::testType(), CORE_Integer::toHexString(), and CORE_Integer::toString().
◆ getMaxUInt()
|
inlinestaticinherited |
get the max value for tUInt type
- Returns
- the max value for tUInt type
Referenced by EMM_Array< tCellFlag >::loadFromFile(), EMM_RealField::loadFromFile(), and CORE_Test::testType().

◆ getMaxUInteger()
|
inlinestaticinherited |
get the max value for the unsigned integer type
- Returns
- the max value for the unsigned integer type
Referenced by MATH_Pn::computeExtrenums(), EMM_MultiScaleGrid::computeLevelsNumber(), EMM_Input::restoreBackup(), MATH_P0::solve(), and CORE_Test::testType().

◆ getMaxULInt()
|
inlinestaticinherited |
get the max value for tULInt type
- Returns
- the max value for tULInt type
Referenced by CORE_Test::testType().
◆ getMaxULLInt()
|
inlinestaticinherited |
get the max value for tULLInt type
- Returns
- the max value for tULLInt type
Referenced by CORE_Test::testType().
◆ getMaxUSInt()
|
inlinestaticinherited |
get the max value for tUSInt type
- Returns
- the max value for tUSInt type
Referenced by CORE_Test::testType().

◆ getMinChar()
|
inlinestaticinherited |
get the min value for tChar type
- Returns
- the min value for tChar type
Referenced by CORE_Test::testType().
◆ getMinDouble()
|
inlinestaticinherited |
get the min value for tDouble type
- Returns
- the min value for tDouble type
Referenced by CORE_Test::testType().

◆ getMinFlag()
|
inlinestaticinherited |
get the min value for the tFlag type
- Returns
- the min value for the tFlag type
Referenced by CORE_Test::testType().
◆ getMinFloat()
|
inlinestaticinherited |
get the min value for tFloat type
- Returns
- the min value for tFloat type
Referenced by CORE_Test::testType().
◆ getMinIndex()
|
inlinestaticinherited |
get the min value for the array/vector indexing type
- Returns
- the min value for the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMinInt()
|
inlinestaticinherited |
get the min value for tInt type
- Returns
- the min value for tInt type
Referenced by CORE_Test::testType().
◆ getMinInteger()
|
inlinestaticinherited |
get the min value for the integer type
- Returns
- the minin value for the integer type
Referenced by CORE_Test::testType().

◆ getMinLDouble()
|
inlinestaticinherited |
get the min value for tLDouble type
- Returns
- the min value for tLDouble type
Referenced by CORE_Test::testType().

◆ getMinLInt()
|
inlinestaticinherited |
get the min value for tLInt type
- Returns
- the min value for tLInt type
Referenced by CORE_Test::testType().
◆ getMinLLInt()
|
inlinestaticinherited |
get the min value for tLLInt type
- Returns
- the min value for tLLInt type
Referenced by CORE_Test::testType().

◆ getMinReal()
|
inlinestaticinherited |
get the min value for the real type
- Returns
- the min value for the real type
Referenced by CORE_Test::testType().
◆ getMinSInt()
|
inlinestaticinherited |
get the min value for tSInt type
- Returns
- the min value for tSInt type
Referenced by CORE_Test::testType().
◆ getMinUChar()
|
inlinestaticinherited |
get the min value for tUChar type
- Returns
- the min value for tUChar type
Referenced by CORE_Test::testType().
◆ getMinUIndex()
|
inlinestaticinherited |
get the min value for difference the array/vector indexing type
- Returns
- the min value for difference the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMinUInt()
|
inlinestaticinherited |
get the min value for tUInt type
- Returns
- the min value for tUInt type
Referenced by CORE_Test::testType().
◆ getMinUInteger()
|
inlinestaticinherited |
get the min value for the unsigned integer type
- Returns
- the min value for the unsigned integer type
Referenced by CORE_Test::testType().

◆ getMinULInt()
|
inlinestaticinherited |
get the min value for tULInt type
- Returns
- the min value for tULInt type
Referenced by CORE_Test::testType().

◆ getMinULLInt()
|
inlinestaticinherited |
get the min value for tULLInt type
- Returns
- the min value for tULLInt type
Referenced by CORE_Test::testType().
◆ getMinUSInt()
|
inlinestaticinherited |
get the min value for tUSInt type
- Returns
- the min value for tUSInt type
Referenced by CORE_Test::testType().
◆ getOut()
|
inlinestaticinherited |
◆ getPointerAddress()
|
inlineinherited |
return the identity string of the object
- Returns
- the identity string of the object
References CORE_Object::pointer2String().

◆ getRealEpsilon()
|
inlinestaticinherited |
get the eps which is the difference between 1 and the least value greater than 1 that is representable.
- Returns
- the eps which is the difference between 1 and the least value greater than 1 that is representable.
Referenced by MATH_P4::solveP4De(), and CORE_Test::testType().
◆ getRealInfinity()
|
inlinestaticinherited |
get the infinity value
- Returns
- the inifinity value for the real type
Referenced by BrentFunction::BrentFunction(), EMM_OperatorsTest::compareDiscretizedData(), EMM_IterativeTimeStep::EMM_IterativeTimeStep(), EMM_SLElementaryDemagnetizedMatrix::Kxy(), NRFunction::NRFunction(), EMM_PolynomialInterpolationTimeStep::optimizeTimeFunction(), and CORE_Test::testType().
◆ getSearchingPaths()
|
inherited |
get the path fro seaching the files
- Parameters
-
vpaths the vectors of searching paths
References tString, and tUSInt.
Referenced by EMM_ElementaryTest::defaultBackupTest(), EMM_ElementaryTest::defaultTest(), EMM_DemagnetizedTest::demagnetizedTestCase(), EMM_DisplacementWaveTest::elasticWaveTest(), EMM_DemagnetizedPeriodicalTest::HTest(), EMMH_HysteresisTest::hysteresisDefaultCycleTest(), EMM_WaveTest::load(), EMM_ElementaryTest::magnetostrictionBackupTest(), EMM_Test::New(), EMM_DemagnetizedPeriodicalTest::periodicalDemagnetizedTestCase(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_Test::searchPath(), EMM_CaseTest::testCase(), EMM_ODETest::testODE(), EMM_FieldTest::testRealArray(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().
◆ getSharedPointer() [1/2]
|
inlineinherited |
get the shared pointer of this class into p
- Parameters
-
p : shared pointer of the class This
Referenced by CORE_Map< Key, Value >::getSharedPointer(), CORE_ArrayList< tString >::getSharedPointer(), EMM_Array< tCellFlag >::getSharedPointer(), CORE_Array< tCellFlag >::getSharedPointer(), CORE_MorseArray< tUChar >::getSharedPointer(), CORE_Vector< T >::getSharedPointer(), and CORE_Object::printObjectsInMemory().
◆ getSharedPointer() [2/2]
|
inlineinherited |
get the shared pointer of this class into p
- Parameters
-
p : shared pointer of the class This
◆ getThread()
|
inlinestaticinherited |
get the profilier
- Returns
- the profiler
Referenced by MATH_MaskVector::add(), MATH_Vector::add(), EMM_DisplacementFEMOperator::addBoundaryElasticStress(), EMM_DisplacementFEMOperator::buildDataOnNeumannBoundaryFaces(), EMM_DisplacementFVMOperator::computeCineticEnergy(), EMM_DisplacementFVMOperator::computeElasticStress(), EMM_DisplacementFEMOperator::computeElasticStress(), EMM_DisplacementFVMOperator::computeElasticTensor(), EMM_DisplacementFEMOperator::computeElasticTensor(), EMM_StaticMagneticTensorOperator::computeEnergy(), EMM_CubicAnisotropyOperator::computeEnergy(), EMM_MagnetostrictionOperator::computeEnergy(), EMM_DisplacementOperator::computeEnergy(), EMM_AnisotropyOperator::computeEnergyWithMagneticExcitation(), EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), EMM_DisplacementFEMOperator::computeEquilibriumMatrixDiagonalConditioner(), EMM_FullExchangeOperator::computeMagneticExcitationField(), EMM_StaticMagnetostrictionOperator::computeMagneticExcitationField(), EMM_LinearAnisotropyOperator::computeMagneticExcitationField(), EMM_StaticMagneticTensorOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationField(), EMM_MinimalExchangeOperator::computeMagneticExcitationField(), EMM_AnisotropyOperator::computeMagneticExcitationField(), EMM_MagnetostrictionOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_AnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_DisplacementFVMOperator::computeMagneticStress(), EMM_DisplacementFEMOperator::computeMagneticStress(), EMM_OptimalTimeStep::computeOptimalTimeStep(), EMM_DisplacementFEMOperator::computeStressConstraintEnergy(), EMM_FullExchangeOperator::discretize(), EMM_MinimalExchangeOperator::discretize(), EMM_CondensedMassMatrix::discretize(), EMM_LinearAnisotropyOperator::discretize(), EMM_AnisotropyOperator::discretize(), EMM_DemagnetizedOperator::discretize(), EMMG_SLDemagnetizedOperator::discretize(), EMM_LandauLifschitzSystem::discretize(), MATH_Vector::divide(), MATH_MaskVector::dot(), MATH_Vector::dot(), EMM_4SymmetricTensors::doubleDot(), EMM_4Tensors::doubleDotCrossDoubleDotScalar(), EMM_4Tensors::doubleDotCrossProduct(), EMM_4Tensors::doubleDotCrossSquaredScalar(), EMM_4Tensors::doubleDotProduct(), MATH_Vector::init(), MATH_MaskVector::init(), EMM_LandauLifschitzODE_RK::integrateMagnetizationFieldAtTime(), EMM_DisplacementFVM_Interpolator::interpolateUAtVertices(), EMMG_SLDemagnetizedOperator::localAssembly(), EMM_DisplacementOperator::nullProjectionOnDirichletBoundary(), EMM_DisplacementOperator::periodicProjection(), EMM_2PackedSymmetricTensors::product(), EMM_CanonicalMassMatrix::product(), MATH_FullMatrix::product(), EMM_CondensedMassMatrix::product(), EMM_BlockMassMatrix::product(), MATH_MorseMatrix::product(), EMMG_SLDemagnetizedOperator::product(), EMM_DisplacementOperator::projectionOnDirichletBoundary(), EMM_LandauLifschitzSystem::resetOperatorsToInitialState(), EMM_DisplacementFVMOperator::setBoundaryFaceTypes(), FFTW_MultiDFTs::setFFT(), FFTW_MultiLevelsDFT::setFFT(), FFTW_MultiLevelsDFT::setLevels(), FFTW_MultiDFTs::setPlan(), FFTW_MultiLevelsDFT::setPlan(), EMM_CondensedMassMatrix::solve(), EMM_LandauLifschitzODE::solveODE(), EMM_4SymmetricTensors::squaredDoubleDot(), EMM_4Tensors::squaredDoubleDotCrossScalar(), EMM_4Tensors::squaredDoubleDotScalar(), EMM_CanonicalMassMatrix::symmetricDot(), EMM_CondensedMassMatrix::symmetricDot(), EMM_BlockMassMatrix::symmetricDot(), FFTW_Test::test(), MATH_SolverTest::test(), EMM_ODETest::testODE(), and EMM_Grid3D::updateLimitConditionOnPoints().

◆ getTypeName()
|
inlinestaticinherited |
◆ is32Architecture()
|
inlinestaticinherited |
return true if the machine is a 32 bits machine
- Returns
- true is the computing is done in a 32 bits machine
References CORE_Object::pointer2String(), CORE_Object::printObjectsInMemory(), and tString.
Referenced by CORE_Test::testType().


◆ is64Architecture()
|
inlinestaticinherited |
return true if the machine is a 64 bits machine
- Returns
- true is the computing is done in a 64 bits machine
Referenced by EMM_VTK::getVTKType(), and CORE_Test::testType().
◆ isInBox()
return true if x[k] is in the [0,dim[k]] for all k in [0,3[
- Parameters
-
dim dimension of the parallelepiped cube x coordinates of the point
- Returns
- trie if the point x is in the box
References tBoolean, and tUSInt.
Referenced by EMM_Test::createBox(), EMM_Test::createCube(), and EMM_Test::New().

◆ isInstanceOf() [1/2]
|
inlineinherited |
test if the clas T is an instance of this class
- Returns
- true if the object is an instance of T
References null.
Referenced by MATH_ToeplitzTest::toeplitzTest().

◆ isInstanceOf() [2/2]
test if the object is an instance of className
- Parameters
-
name name of the class
- Returns
- true if the object is an instance of class Name
References CORE_Object::getIdentityString().

◆ isMemoryChecked()
|
inlinestaticinherited |
get if the memory checking is used
- Returns
- true: if the memory checking is used.
References CORE_Object::getClassName(), CORE_Object::mIsMemoryTesting, and tString.
Referenced by main().


◆ linearPieceWise_function()
|
staticprotectedinherited |
References tReal, and tUInteger.
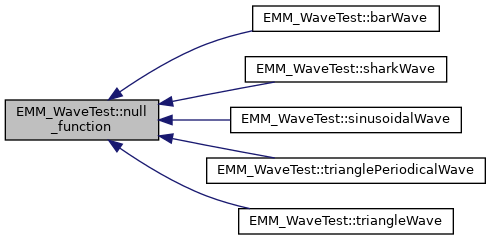
Referenced by EMM_WaveTest::barWave(), EMM_WaveTest::shark_function(), and EMM_WaveTest::triangle_function().
◆ load()
|
protectedinherited |
load the data from txt file
- Parameters
-
optionFile name of the file containing lines key=value The keys are - "dirichlet0"
- "dirichlet1"
- "L"
- "nPoints"
- "Umax"
- "C"
- "nTimes"
- "cfl"
- "txt-output"
path the path where the option file is found isTXTOutput : true to save the evolution in txt files isPeriodic : true if the domain is supposed to be periodic dirichletLC : read the dirichlet conditions on x=0 and x=L L the length of the 1D-domain nPoints : number of discretized points on x Umax the maximum amplitude of U C the celerity of the wave nTimes the number of time steps cfl the cfl condition <=1
- Returns
- true if the loading succeeded
References EMM_Test::getSearchingPaths(), CORE_Integer::parseInt(), CORE_Real::parseReal(), EMM_Test::searchPath(), CORE_String::string2Boolean(), tChar, tIndex, tString, tUIndex, and tUInt.
Referenced by EMM_WaveTest::barWave(), EMM_WaveTest::sharkWave(), EMM_WaveTest::sinusoidalWave(), EMM_WaveTest::trianglePeriodicalWave(), and EMM_WaveTest::triangleWave().
◆ New()
|
inlinestatic |
create a test class
References EMM_WaveFEMTest().
Referenced by EMM_DisplacementWaveTest::test().


◆ null_function()
Referenced by EMM_WaveTest::barWave(), EMM_WaveTest::sharkWave(), EMM_WaveTest::sinusoidalWave(), EMM_WaveTest::trianglePeriodicalWave(), and EMM_WaveTest::triangleWave().
◆ out()
|
inlinestaticinherited |
get the output
- Returns
- the output stream
Referenced by EMM_Matter::adimensionize(), EMM_DisplacementFVMOperator::backup(), EMM_DisplacementOperator::backup(), MATH_ElementaryMultiLevelsToeplitzMatrix::buildSpectralVectorProjector(), EMM_Test::caseTest(), EMM_Test::caseTests(), EMM_MatterField::computeAnisotropyDirectionsField(), EMM_OptimalTimeStep::computeOptimalTimeStep(), MATH_MultiLevelsToeplitzMatrix::copy(), CORE_Exception::CORE_Exception(), EMM_MatterField::createAnisotropyOperator(), CORE_Run::createIO(), EMM_ElementaryTest::defaultBackupTest(), EMM_ElementaryTest::defaultTest(), MATH_MultiLevelsFFTToeplitzMatrix::diagonalize(), EMM_DisplacementFVMOperator::discretize(), EMM_MagnetostrictionOperator::discretize(), EMM_DisplacementFEMOperator::discretize(), EMM_4SymmetricTensors::doubleDot(), EMM_4Tensors::doubleDotCrossDoubleDotScalar(), EMM_TensorsTest::doubleDotCrossDoubleDotScalarTests(), EMM_4Tensors::doubleDotCrossProduct(), EMM_TensorsTest::doubleDotCrossProductTests(), EMM_4Tensors::doubleDotCrossSquaredScalar(), EMM_TensorsTest::doubleDotCrossSquaredScalarTests(), EMM_4Tensors::doubleDotProduct(), EMM_TensorsTest::doubleDotProductTests(), EMM_DisplacementWaveTest::elasticWaveTest(), EMM_Test::elementaryTests(), FFTW_Test::fftwTutorial(), MATH_IntegrationTest::gaussLegendreTest(), EMM_MagnetostrictionTest::HComputingTest(), EMM_DemagnetizedPeriodicalTest::HTest(), EMMH_HysteresisTest::hysteresisDefaultCycleTest(), EMM_TensorsTest::initializationTests(), EMM_MultiScaleGrid::initialize(), EMM_MultiScaleSDGrid::initialize(), EMM_MatterField::loadFromANIFile(), EMM_AnisotropyDirectionsField::loadFromFile(), EMM_Matter::loadFromFile(), EMM_Grid3D::loadFromGEOFile(), EMM_MatterField::loadFromLOCFile(), EMM_Array< tCellFlag >::loadFromStream(), EMM_Matter::loadFromStream(), EMM_Matter::loadMattersFromFile(), EMM_Run::loadSystemFromOptions(), EMM_ElementaryTest::magnetostrictionBackupTest(), CORE_Run::make(), EMMH_Run::makeHysteresis(), EMM_Run::makeRun(), CORE_Run::makeType(), EMM_ElementaryTest::optionsTest(), MATH_PolynomialTest::P4Tests(), EMM_Test::primaryTests(), EMM_LandauLifschitzSystem::printLog(), CORE_Run::printOptions(), EMM_2PackedSymmetricTensors::product(), EMMG_SLDemagnetizedOperator::projectionOnSpectralSpace(), CORE_Run::readOptionsFromCommandLine(), CORE_Test::readVectorTest(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_DisplacementFVMOperator::restore(), EMM_DisplacementOperator::restore(), EMM_Input::restoreBackup(), EMMH_Hysteresis::run(), EMM_Output::save(), EMM_AnisotropyDirectionsField::saveToFile(), EMM_MatterField::saveToFile(), EMM_Grid3D::saveToGEOFile(), CORE_IOTest::searchTest(), EMMH_Hysteresis::setInitialMagnetizationField(), MATH_MultiLevelsToeplitzMatrix::setLevels(), EMM_4SymmetricTensors::squaredDoubleDot(), EMM_4Tensors::squaredDoubleDotCrossScalar(), EMM_TensorsTest::squaredDoubleDotCrossScalarTests(), EMM_4Tensors::squaredDoubleDotScalar(), EMM_TensorsTest::squaredDoubleDotScalarTests(), EMM_TensorsTest::squaredDoubleDotTests(), EMM_MatterTest::testAdimensionize(), EMM_MatterTest::testANIFile(), CORE_Test::testComplex(), CORE_Test::testDateWeek(), FFTW_Test::testDFT(), EMM_MatterTest::testIO(), EMM_ODETest::testODE(), CORE_Test::testOut(), CORE_Test::testReal(), EMM_FieldTest::testRealArray(), EMM_Grid3DTest::testSegment(), EMM_Grid3DTest::testThinSheet(), CORE_Test::testTime(), CORE_Test::testType(), MATH_FullMatrix::toString(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().

◆ performanceTest()
|
virtualinherited |
make the perfomance tests
- Parameters
-
runner the associated runner options the option sof the test to run
- Returns
- true if succeeds
Reimplemented from CORE_Test.
Reimplemented in EMM_OperatorsTest.
References CORE_Run::getClassFactory(), tBoolean, and EMM_Test::test().
Referenced by EMM_Test::New().

◆ pointer2String()
|
staticinherited |
return the string representation of a pointer
- Parameters
-
obj : oject to get the string pointer
- Returns
- the string pointer of the object
References tString.
Referenced by CORE_Object::CORE_Object(), CORE_Object::getIdentityString(), CORE_Object::getPointerAddress(), CORE_Object::is32Architecture(), and CORE_Object::~CORE_Object().

◆ printObjectsInMemory() [1/2]
|
staticinherited |
print object in memory
- Parameters
-
f : output to print the objects in memory
References CORE_Object::getIdentityString(), CORE_Object::getSharedPointer(), CORE_Object::mIsMemoryTesting, CORE_Object::mObjects, and tInteger.

◆ printObjectsInMemory() [2/2]
|
inlinestaticinherited |
print object in memory in the standart output
Referenced by CORE_Object::is32Architecture(), and main().
◆ resetOut()
|
inlinestaticinherited |
◆ resetThread()
|
inlinestaticinherited |
◆ save() [1/2]
|
protectedinherited |
save the displacement at time with space space of dx
- Parameters
-
fileName name of the file to save dx the space step U the displacement U nPts : the number of space step
References tReal, and tUIndex.
Referenced by EMM_WaveFDMTest::waveSystemP1Propagation(), EMM_WaveFDMTest::waveSystemP2Propagation(), EMM_WaveFDMTest::waveTE2Propagation(), and waveTE2Propagation().

◆ save() [2/2]
◆ searchPath()
set the path to find the file with name fileName
- Parameters
-
fileName name of the file
- Returns
- the path to find the file. Return empty path if not found
References CORE_IO::exists(), and EMM_Test::getSearchingPaths().
Referenced by EMM_Test::computeMField(), EMM_ElementaryTest::defaultBackupTest(), EMM_ElementaryTest::defaultTest(), EMM_DemagnetizedTest::demagnetizedTestCase(), EMM_DisplacementWaveTest::elasticWaveTest(), EMM_DemagnetizedPeriodicalTest::HTest(), EMMH_HysteresisTest::hysteresisCycleTest(), EMMH_HysteresisTest::hysteresisDefaultCycleTest(), EMM_WaveTest::load(), EMM_ElementaryTest::magnetostrictionBackupTest(), EMM_Test::New(), EMM_DemagnetizedPeriodicalTest::periodicalDemagnetizedTestCase(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_MatterTest::testAdimensionize(), EMM_MatterTest::testANIFile(), EMM_CaseTest::testCase(), EMM_MatterTest::testIO(), EMM_ODETest::testODE(), EMM_FieldTest::testRealArray(), EMM_Grid3DTest::testSegment(), EMM_Grid3DTest::testThinSheet(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().

◆ setIsCondensedMassMatrix()
|
inline |
set true if the Mass Matrix is condensed or not
- Parameters
-
isCondensed true if the mass matrix is diagonal
References computeCondensedMassMatrix(), computeMassMatrix(), computeStressMatrix(), computeWaveAtFirstTime(), tBoolean, tReal, tString, tUIndex, and waveTE2Propagation().
◆ setIsMemoryChecked()
|
inlinestaticinherited |
set if the memory checking is used
- Parameters
-
v : true to check memory
Referenced by main().

◆ setOut()
|
inlinestaticinherited |
◆ setThis()
|
inlineprotectedinherited |
set this weak shared pointer called toDoAfterThis setting method
- Parameters
-
p : shared pointer of the class This
References CORE_Object::toDoAfterThisSetting().

◆ setThread()
|
inlinestaticinherited |
set the thread
- Parameters
-
thread the shared pointer to the thread
References null.
Referenced by EMM_Run::EMM_Run(), EMM_TensorsRun::EMM_TensorsRun(), and MATH_SolverRun::MATH_SolverRun().
◆ shark_function()
References EMM_WaveTest::linearPieceWise_function(), tReal, and tUInteger.
Referenced by EMM_WaveTest::sharkWave().


◆ sharkWave() [1/2]
References EMM_Test::caseTest(), CORE_Array< T >::initArray(), EMM_WaveTest::load(), EMM_WaveTest::null_function(), CORE_Array< T >::setSize(), EMM_WaveTest::shark_function(), tBoolean, tReal, tString, tUIndex, tUSInt, EMM_WaveTest::waveSystemP1Propagation(), EMM_WaveTest::waveSystemP2Propagation(), and EMM_WaveTest::waveTE2Propagation().
◆ sharkWave() [2/2]
|
inlineprotectedvirtual |
Implements EMM_WaveTest.
References EMM_WaveTest::sharkWave().

◆ sinusoidal_function()
|
staticprotectedinherited |
References tReal.
Referenced by EMM_WaveTest::sinusoidalWave().

◆ sinusoidalWave() [1/2]
References EMM_Test::caseTest(), CORE_Array< T >::initArray(), EMM_WaveTest::load(), EMM_WaveTest::null_function(), CORE_Array< T >::setSize(), EMM_WaveTest::sinusoidal_function(), tBoolean, tReal, tString, tUIndex, tUSInt, EMM_WaveTest::waveSystemP1Propagation(), EMM_WaveTest::waveSystemP2Propagation(), and EMM_WaveTest::waveTE2Propagation().
◆ sinusoidalWave() [2/2]
|
inlineprotectedvirtual |
Implements EMM_WaveTest.
References EMM_WaveTest::sinusoidalWave().

◆ SP_OBJECT()
|
private |
◆ test()
|
virtualinherited |
make the test
- Returns
- true if succeeds
Reimplemented from EMM_Test.
References EMM_WaveTest::barWave(), EMM_WaveTest::sharkWave(), EMM_WaveTest::sinusoidalWave(), tBoolean, EMM_WaveTest::trianglePeriodicalWave(), EMM_WaveTest::triangleWave(), and tString.
◆ testType()
|
inherited |
test type
References CORE_Object::getDoubleEpsilon(), CORE_Object::getFloatEpsilon(), CORE_Object::getLDoubleEpsilon(), CORE_Object::getMaxChar(), CORE_Object::getMaxDouble(), CORE_Object::getMaxFlag(), CORE_Object::getMaxFloat(), CORE_Object::getMaxIndex(), CORE_Object::getMaxInt(), CORE_Object::getMaxInteger(), CORE_Object::getMaxLDouble(), CORE_Object::getMaxLInt(), CORE_Object::getMaxLLInt(), CORE_Object::getMaxReal(), CORE_Object::getMaxSInt(), CORE_Object::getMaxUChar(), CORE_Object::getMaxUIndex(), CORE_Object::getMaxUInt(), CORE_Object::getMaxUInteger(), CORE_Object::getMaxULInt(), CORE_Object::getMaxULLInt(), CORE_Object::getMaxUSInt(), CORE_Object::getMinChar(), CORE_Object::getMinDouble(), CORE_Object::getMinFlag(), CORE_Object::getMinFloat(), CORE_Object::getMinIndex(), CORE_Object::getMinInt(), CORE_Object::getMinInteger(), CORE_Object::getMinLDouble(), CORE_Object::getMinLInt(), CORE_Object::getMinLLInt(), CORE_Object::getMinReal(), CORE_Object::getMinSInt(), CORE_Object::getMinUChar(), CORE_Object::getMinUIndex(), CORE_Object::getMinUInt(), CORE_Object::getMinUInteger(), CORE_Object::getMinULInt(), CORE_Object::getMinULLInt(), CORE_Object::getMinUSInt(), CORE_Object::getRealEpsilon(), CORE_Object::getRealInfinity(), CORE_Object::is32Architecture(), CORE_Object::is64Architecture(), CORE_Object::out(), CORE_Out::setVerbose(), tBoolean, tChar, tComplex, tDouble, tFlag, tFloat, tIndex, tInt, tInteger, tLDouble, tLInt, tLLInt, tReal, tSInt, tString, tUChar, tUIndex, tUInt, tUInteger, tULInt, tULLInt, and tUSInt.
Referenced by CORE_Test::New(), and CORE_Test::test().

◆ toDoAfterThisSetting()
|
inlineprotectedvirtualinherited |
method called after setThis() method this method can oly be called once.
Reimplemented in EMM_DisplacementOperator, EMM_DisplacementFVMOperator, EMM_GaussLegendreRelaxation, EMM_GradGaussLegendreRelaxation, and EMM_Object.
Referenced by CORE_Object::setThis().

◆ toString()
|
inlinevirtualinherited |
return the string representation of the object node
- Returns
- the string representation of the object node
Reimplemented in EMM_DisplacementOperator, EMM_LandauLifschitzSystem, CORE_Array< T >, CORE_Array< tReal >, CORE_Array< tUInteger >, CORE_Array< tString >, CORE_Array< tLimitCondition >, CORE_Array< tUIndex >, CORE_Array< tUChar >, CORE_Array< tCellFlag >, EMM_Grid3D, CORE_Time, CORE_Vector< T >, EMM_Matter, CORE_Out, EMM_DisplacementFEMOperator, EMM_RealField, EMM_DisplacementFVMOperator, CORE_MorseArray< T >, CORE_MorseArray< tReal >, CORE_MorseArray< tUIndex >, CORE_MorseArray< tUChar >, EMM_MagnetostrictionOperator, MATH_MultiLevelsToeplitzMatrix, FFTW_ComplexArray, MATSGN_ComplexArray, EMM_MatterField, CORE_Color, FFTW_Complex, EMM_MultiScaleGrid, MATSGN_Complex, EMM_DisplacementFVM_VTEGROperator, EMM_CondensedMassMatrix, EMM_LandauLifschitzFunction, EMM_Tensors, EMM_DisplacementFVM_SSGROperator, EMMG_SLDemagnetizedOperator, EMM_BlockMassMatrix, CORE_Array2D< T >, EMM_DisplacementFVM_STEGROperator, EMMH_HysteresisFile, EMM_IterativeTimeStep, CORE_SharedPointersVMap< Key, Value >, CORE_SharedPointersVMap< tString, const CORE_Object >, CORE_SharedPointersVMap< tString, CORE_Object >, EMM_AnisotropyDirectionsField, EMM_DemagnetizedOperator, CORE_SharedPointersListVMap< Key, Value >, CORE_String, EMM_OptimalTimeStep, MATH_MaskArrayVector, CORE_SharedPointersKVMap< Key, Value >, MATH_ArrayVector, EMM_Stepper, EMM_CanonicalMassMatrix, MATH_Pn, MATH_FullMatrix, EMMG_SLPeriodicMultiScale, EMM_HyperElasticMatter, MATH_Matrix, CORE_Array3D< T >, EMM_CubicElasticMatter, CORE_Complex, CORE_Integer, CORE_Real, and EMM_MagnetostrictiveMatter.
References CORE_Object::getIdentityString().
Referenced by CORE_Out::genericPrint(), EMM_VelocitySolverTest::massMatrixTrivialSolverTest(), MATH_ConjugateGradient::solve(), CORE_SharedPointersKVMap< Key, Value >::toString(), CORE_SharedPointersListVMap< Key, Value >::toString(), CORE_SharedPointersVMap< tString, CORE_Object >::toString(), EMM_MagnetostrictionOperator::toString(), EMM_Matter::toString(), and EMM_DisplacementOperator::toString().

◆ triangle_function()
|
staticprotectedinherited |
References EMM_WaveTest::linearPieceWise_function(), tReal, and tUInteger.
Referenced by EMM_WaveTest::trianglePeriodicalWave(), and EMM_WaveTest::triangleWave().


◆ trianglePeriodicalWave() [1/2]
References EMM_Test::caseTest(), CORE_Array< T >::initArray(), EMM_WaveTest::load(), EMM_WaveTest::null_function(), CORE_Array< T >::setSize(), tBoolean, tReal, EMM_WaveTest::triangle_function(), tString, tUIndex, tUSInt, EMM_WaveTest::waveSystemP1Propagation(), EMM_WaveTest::waveSystemP2Propagation(), and EMM_WaveTest::waveTE2Propagation().
◆ trianglePeriodicalWave() [2/2]
|
inlineprotectedvirtual |
Implements EMM_WaveTest.
References EMM_WaveTest::trianglePeriodicalWave().

◆ triangleWave() [1/2]
References EMM_Test::caseTest(), CORE_Array< T >::initArray(), EMM_WaveTest::load(), EMM_WaveTest::null_function(), CORE_Array< T >::setSize(), tBoolean, tReal, EMM_WaveTest::triangle_function(), tString, tUIndex, tUSInt, EMM_WaveTest::waveSystemP1Propagation(), EMM_WaveTest::waveSystemP2Propagation(), and EMM_WaveTest::waveTE2Propagation().
◆ triangleWave() [2/2]
|
inlineprotectedvirtual |
Implements EMM_WaveTest.
References EMM_WaveTest::triangleWave().

◆ waveSystemP1Propagation()
|
inlineprotectedvirtual |
compute the wave at any time from initial conditions U(0,.) and V(0,x) and from dirichlet limit conditions 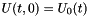 or/and
or/and 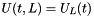 and/or Neumann limit conditions
and/or Neumann limit conditions 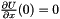 or/and
or/and 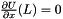 based on solving a system (U,V) :
based on solving a system (U,V) :
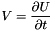
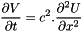 .
.
This relations imply : 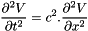
- Parameters
-
isTXTOutput : true to save evolution in TXT files prefix prefix for saving file dirichletLC limit condition of dirichlet U_0 : function depending on time t at x=0 if dirichlet condition U_L : function depending on time t at x=L if dirichlet condition c the celerity L the length of the bar dt time step nT : the number of time steps U : initial value of U on x a t=0, returned U(x,t) V : initial value of velocity at t=0 for all x in [0,L[, returned V(x,t)
Not yet implemented
Implements EMM_WaveTest.
◆ waveSystemP2Propagation()
|
inlineprotectedvirtual |
compute the wave at any time from initial conditions U(0,.) and V(0,x) and from dirichlet limit conditions 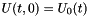 or/and
or/and 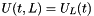 and/or Neumann limit conditions
and/or Neumann limit conditions 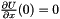 or/and
or/and 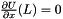 based on solving a system (V,W)
based on solving a system (V,W)
- Parameters
-
isTXTOutput : true to save evolution in TXT files prefix prefix for saving file dirichletLC limit condition of dirichlet U_0 : function depending on time t at x=0 if dirichlet condition U_L : function depending on time t at x=L if dirichlet condition c the celerity L the length of the bar cfl condition for convergence cfl=C*dt/dx<=1 nT : the number of time steps U : initial value of U on x a t=0, returned U(x,t) V : initial value of velocity at t=0 for all x in [0,L[, returned V(x,t)
Not yet implemented
Implements EMM_WaveTest.
◆ waveTE2Propagation()
|
protectedvirtual |
compute the wave at any time from initial conditions U(0,.) and V(0,x) and from dirichlet limit conditions 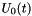 or/and
or/and 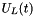 and/or Neumann limit conditions
and/or Neumann limit conditions 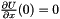 or/and
or/and 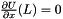 based on Taylor expansion of order 2 for time:
based on Taylor expansion of order 2 for time: 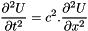
- Parameters
-
isForward : the first displacement is computing at dt if true. Otherwise, the displacement at -dt is built isTXTOutput : true to save evolution in TXT files prefix prefix for saving file isPeriodic to set if the wave is supposed to be periodic dirichletLC limit condition of dirichlet U_0 : function depending on time t at x=0 if dirichlet condition U_L : function depending on time t at x=L if dirichlet condition C the celerity L the length of the bar cfl condition for convergence cfl=C*dt/dx<=1 nT : the number of time steps U : initial value of U on x a t=0, returned U(x,t) V : initial value of velocity at t=0 for all x in [0,L[, returned V(x,t)
compute the displacement U(dt,.) from U(t,.) and U(t-dt,.) with the following formula (see EMM_WaveFEMTest::computeWaveAtFirstTime() ) :
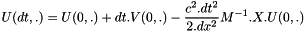
- apply the limit conditions to U(dt)
use the following formula,
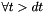 ,
,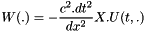 where X is defined in EMM_WaveFEMTest::computeStressMatrix() .
where X is defined in EMM_WaveFEMTest::computeStressMatrix() .
For the Dirichlet points i , force 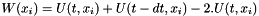 when the limit condition at i
when the limit condition at i 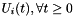 is given.
is given.
then 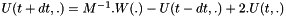 where M is defined in EMM_WaveFEMTest::computeMassMatrix() or EMM_WaveFEMTest::computeCondendedMassMatrix() for the condensed mass diagonal matrix.
where M is defined in EMM_WaveFEMTest::computeMassMatrix() or EMM_WaveFEMTest::computeCondendedMassMatrix() for the condensed mass diagonal matrix.
The stability of the solution is given by finding a solution of the form 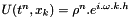 where
where 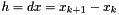 within the preceeding formula. It gives:
within the preceeding formula. It gives:
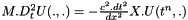
If M is not condensed:
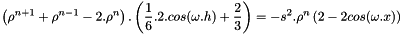 with
with 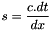 .
.
It leads to 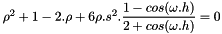
So, 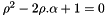 with
with 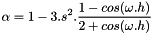 .
.
We habe the discriminant 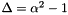 . If the discriminant is positive then
. If the discriminant is positive then 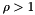 .
.
So to be negative, we have to impose that 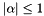 .
.
It leads to 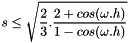 .
.
As the minimum of the 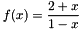 is 2 on x in [-1,1], if
is 2 on x in [-1,1], if 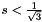 , we have
, we have 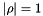 which means that the solution is stable.
which means that the solution is stable.
If M is condensed, we have:
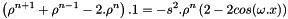 with
with 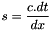 .
.
So we have 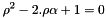 with
with 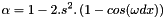 .
.
For the same reason as the not condensed matrix case, if we have 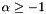 , we have
, we have 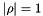 .
.
It leads to 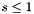 for having a stable solution.
for having a stable solution.
Implements EMM_WaveTest.
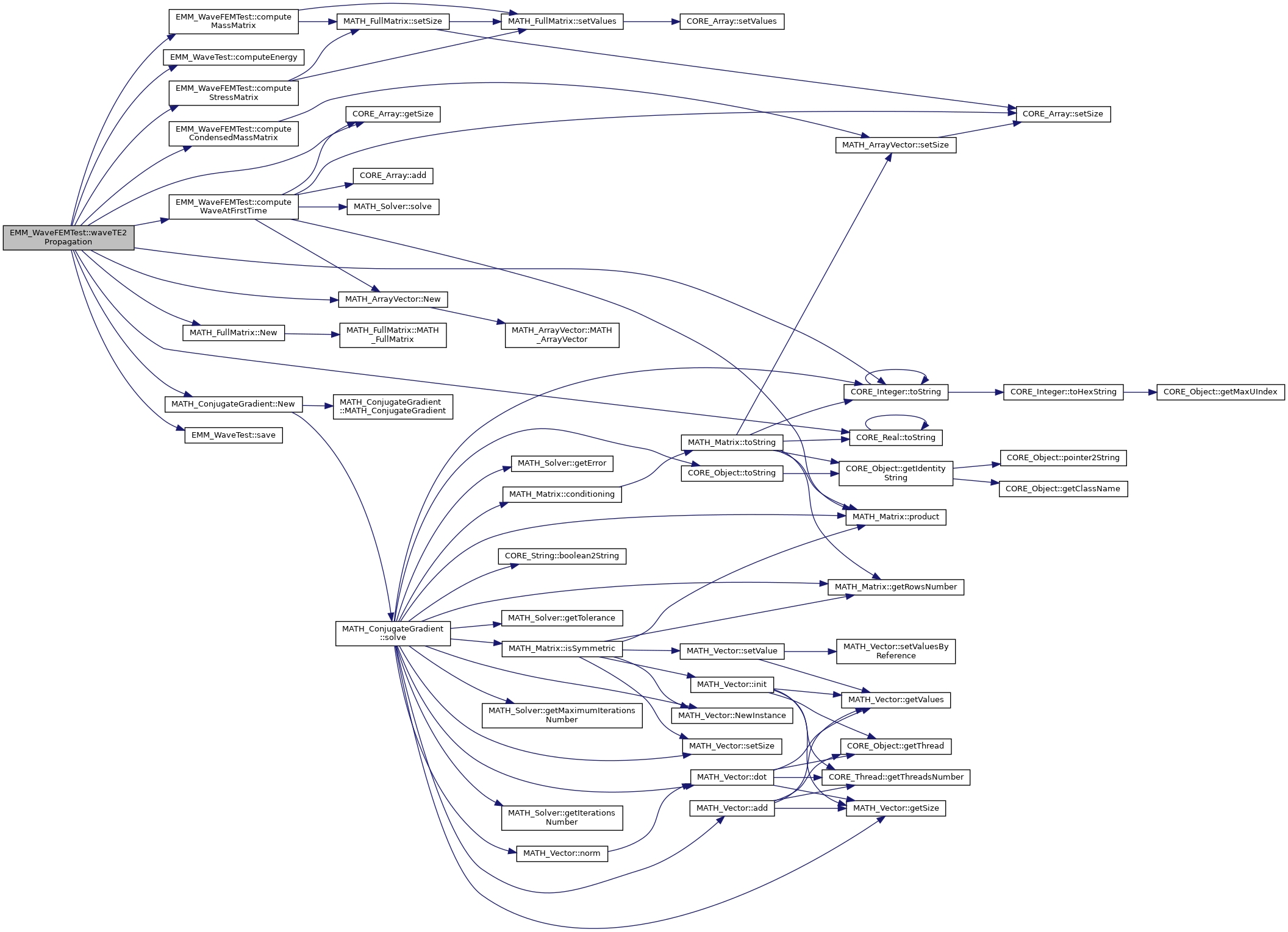
References computeCondensedMassMatrix(), EMM_WaveTest::computeEnergy(), computeMassMatrix(), computeStressMatrix(), computeWaveAtFirstTime(), CORE_Array< T >::getSize(), mIsMassMatrixCondensed, MATH_ArrayVector::New(), MATH_FullMatrix::New(), MATH_ConjugateGradient::New(), EMM_WaveTest::save(), CORE_Real::toString(), CORE_Integer::toString(), tReal, tString, and tUIndex.
Referenced by setIsCondensedMassMatrix().

Member Data Documentation
◆ ALL_TESTS
|
staticinherited |
Referenced by EMM_Test::test().
◆ CASE_TEST
|
staticinherited |
Referenced by EMM_Test::test().
◆ CASE_TESTS
|
staticinherited |
Referenced by EMM_Test::test().
◆ ELEMENTARY_TESTS
|
staticinherited |
Referenced by EMM_Test::test().
◆ mIsMassMatrixCondensed
|
private |
Referenced by EMM_WaveFEMTest(), and waveTE2Propagation().
◆ PRIMARY_TESTS
|
staticinherited |
Referenced by EMM_Test::test().
The documentation for this class was generated from the following files:
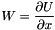
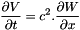
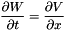


 1.8.13
1.8.13