This class describes the displacement operator defined on the points of the mesh. More...
#include <EMM_DisplacementFEMOperator.h>

Public Member Functions | |
| virtual tBoolean | discretize (const EMM_LandauLifschitzSystem &system) |
| discretize the operator More... | |
| virtual tBoolean | resetToInitialState (const EMM_LandauLifschitzSystem &system) |
| reset the operator to initial state the operator More... | |
| void | setMassMatrixType (const tFlag &t) |
| set the mass matrix type More... | |
| const tFlag & | getMassMatrixType () const |
| get the mass matrix type More... | |
| virtual SP::EMM_MassMatrix | NewMassMatrix () const |
| create the accelerator matrix More... | |
| const tUIndex * | getPointsNumber () const |
| get the points number in each direction More... | |
| const tCellFlag & | getPeriodicIndicator () const |
| get the periodicity indication More... | |
| const EMM_CellFlagArray & | getNeighborsIndicator () const |
return the neighbors indicator in bits 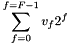 where F is the number of faces per element and where F is the number of faces per element and 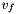 is 1 if there is a neighbor cell with the face f More... is 1 if there is a neighbor cell with the face f More... | |
| virtual tULLInt | getMemorySize () const |
| return the memory size in byte More... | |
| virtual tBoolean | getDataFieldSpace (const tUSInt &index, tString &dataName, tFlag &supportType, tString &dFieldType, tUIndex &n, tDimension &dim) const |
| get the data field at index for saving data in vtk,txt,... files. More... | |
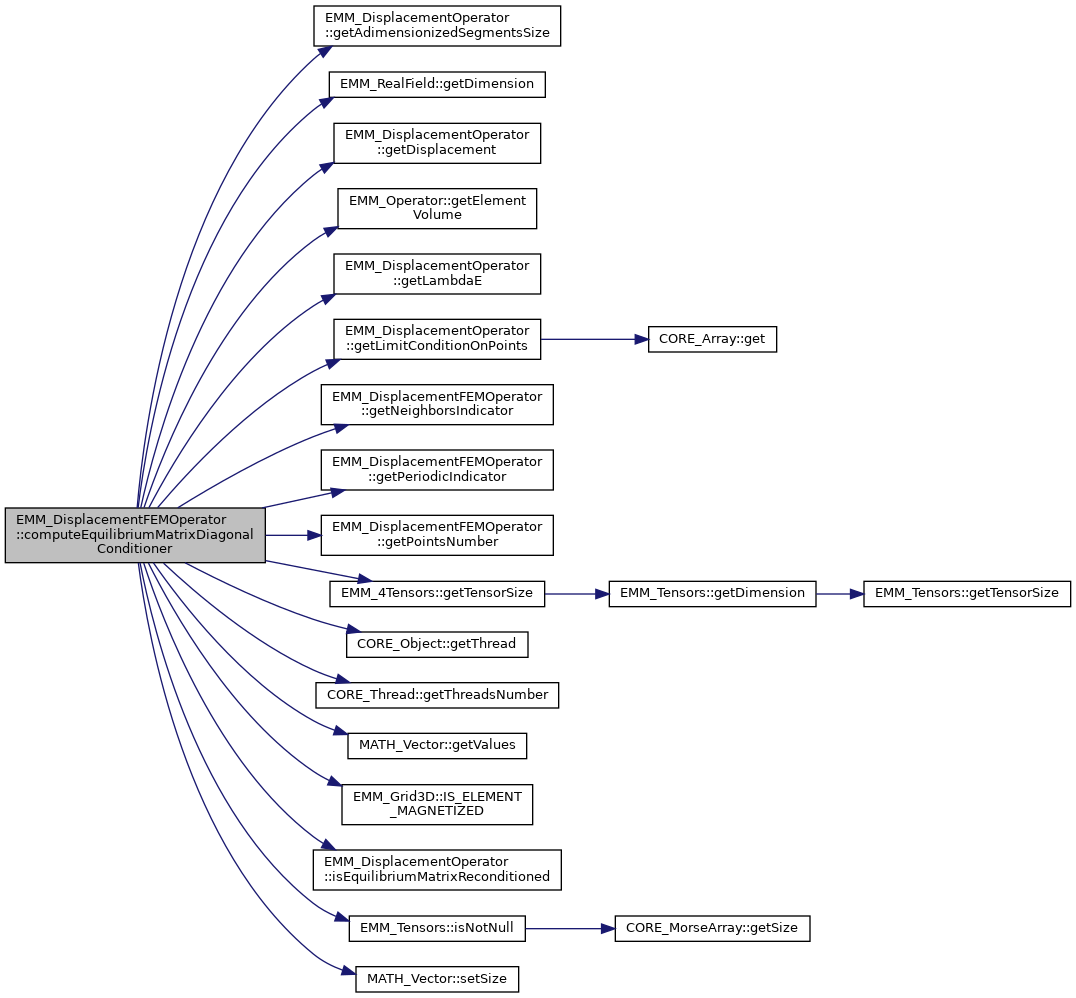
| virtual void | computeEquilibriumMatrixDiagonalConditioner (MATH_Vector &D) const |
| compute the diagonal conditioner More... | |
| virtual tReal | computeCineticEnergy (const EMM_RealField &V) const |
| compute the energy of the magnetostriction operator at current displacement and velocity More... | |
| virtual tReal | computePotentialEnergy (const EMM_RealField &U) const |
| compute the potential energy to the space variation of the displacement More... | |
| tReal | computeStressConstraintEnergy (const EMM_RealField &Uf) const |
| compute the stress constraint energy on boundary More... | |
| virtual tString | toString () const |
| turn the martix into string More... | |
| virtual void | adimensionize (const tReal &Le, const tReal &Ms, const tReal &T, const tReal &L) |
| adimensionize the operator More... | |
| const tReal * | getAdimensionizedSegmentsSize () const |
| get the segments size in all directions More... | |
| const EMM_RealArray & | getAdimensionizedVolumicMass () const |
| get the adimensionized volumic mass per cell More... | |
| const EMM_4SymmetricTensors & | getLambdaE () const |
return the adimensionized elastic tensor distribution 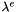 More... More... | |
| const EMM_4Tensors & | getLambdaEDoubleDotLambdaM () const |
return the adimensionized magnetic tensor distribution 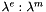 More... More... | |
| const EMM_4Tensors & | getLambdaMDoubleDotLambdaE () const |
return the adimensionized magnetic tensor distribution  More... More... | |
| const EMM_4SymmetricTensors & | getLambdaMDoubleDotLambdaEDoubleDotLambdaM () const |
return the adimensionized magnetic tensor distribution 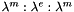 More... More... | |
| void | setInitialDisplacement (const tReal &scale, const tString &dataFile) |
| set initial displacement field. More... | |
| void | setInitialDisplacement (const tReal data[3]) |
| set initial displacement field More... | |
| void | setInitialDisplacement (const tReal U0, const tReal &U1, const tReal &U2) |
| set initial displacement field More... | |
| void | setInitialDisplacement (const EMM_RealField &data) |
| set initial displacement field More... | |
| void | setInitialVelocity (const tReal &scale, const tString &dataFile) |
| set initial velocity field More... | |
| void | setInitialVelocity (const EMM_RealField &data) |
| set initial velocity field More... | |
| void | setInitialVelocity (const tReal data[3]) |
| set initial velocity field More... | |
| void | setInitialVelocity (const tReal &V0, const tReal &V1, const tReal &V2) |
| set initial velocity field More... | |
| void | setLimitConditionOnPoints (const EMM_IntArray &lc) |
| set the limit condition each point is set to More... | |
| void | setLimitConditionOnPoints (const tLimitCondition &lc) |
| set the limit condition to all points More... | |
| void | setConstraints (const tFlag &C, const tString &dataFile) |
| set constraints from file defined on points More... | |
| void | setConstraints (const tFlag &C, const tReal data[3]) |
| set constraints field More... | |
| void | setConstraints (const tFlag &C, const tReal &C0, const tReal &C1, const tReal &C2) |
| set initial constriants field More... | |
| void | setConstraints (const tFlag &C, const EMM_RealField &data) |
| set constraints More... | |
| const tFlag & | getConstraintFaces () const |
get the constraint faces 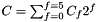 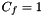 if face f is constrainted More... if face f is constrainted More... | |
| const EMM_RealField & | getConstraints () const |
| get the constraints field for reading More... | |
| EMM_RealField & | getConstraints () |
| get the constraints field for writing More... | |
| const EMM_LimitConditionArray & | getLimitConditionOnPoints () const |
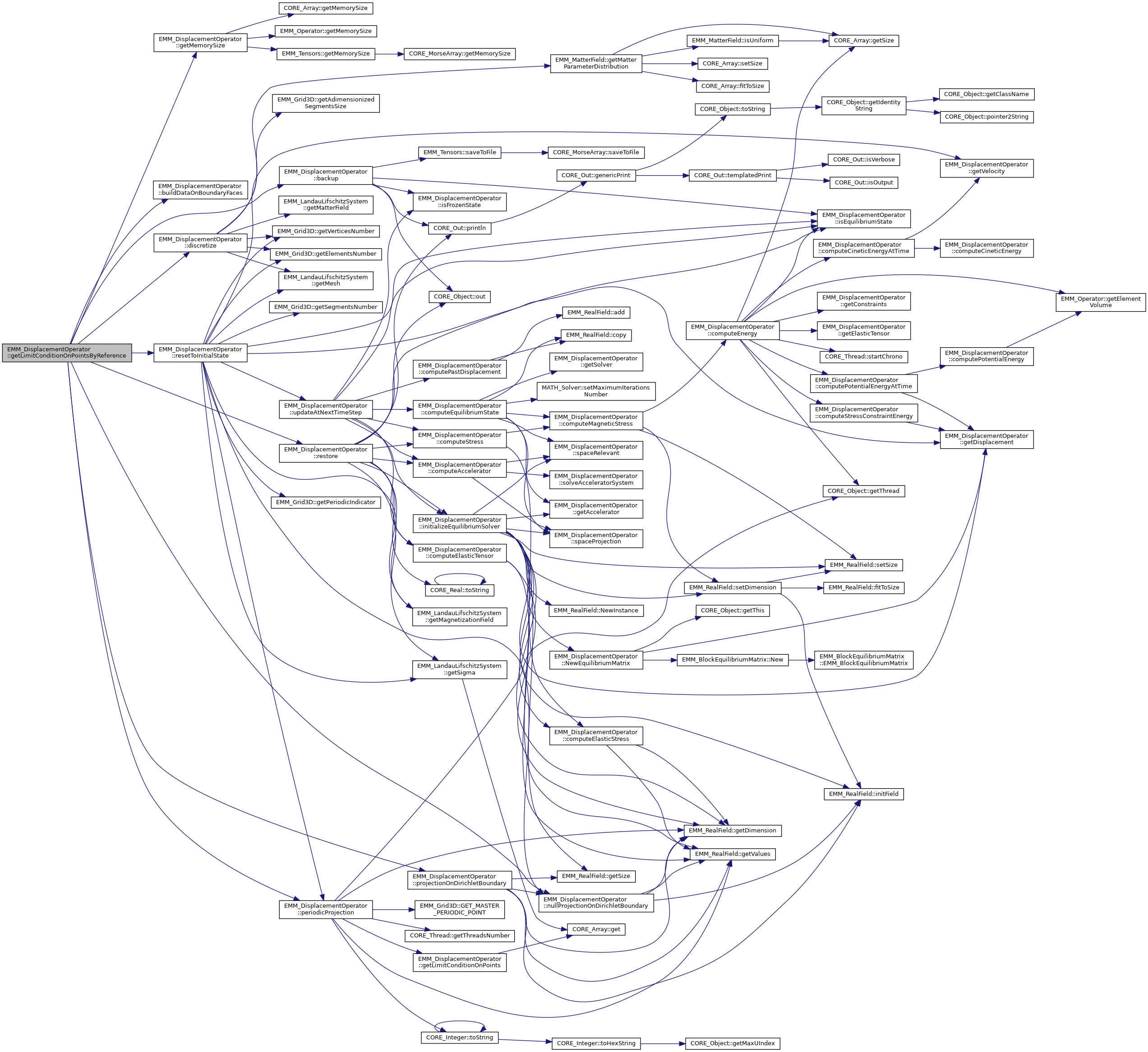
| SPC::EMM_LimitConditionArray | getLimitConditionOnPointsByReference () const |
| void | nullProjectionOnDirichletBoundary (EMM_RealField &V) const |
| project the velocity to 0 on dirichlet boundary points More... | |
| void | nullProjectionOnDirichletBoundary (const tUIndex &nPoints, const tDimension &dim, tReal *V) const |
| project the velocity to 0 on dirichlet boundary points More... | |
| void | projectionOnDirichletBoundary (const EMM_RealField &V0, EMM_RealField &V) const |
| project the velocity to 0 on dirichlet boundary points More... | |
| void | projectionOnDirichletBoundary (const tUIndex &nPoints, const tDimension &dim, const tBoolean &incV0, const tReal *V0, tReal *V) const |
| project the velocity to 0 on dirichlet boundary points More... | |
| void | periodicProjection (const tCellFlag &periodicity, const tUInteger nPoints[3], EMM_RealField &V) const |
| make the periodic projection of the field V More... | |
| virtual tBoolean | backup (const tString &prefix, const tString &suffix, const tString &ext) const |
| backup of the operator data into file(s) used for restoring More... | |
| virtual tBoolean | restore (const EMM_LandauLifschitzSystem &system, const tString &prefix, const tString &suffix, const tString &ext) |
| restore the operator data from file(s) More... | |
| const EMM_2PackedSymmetricTensors & | getElasticTensor () const |
return the elastic tensor 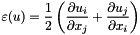 More... More... | |
| virtual tUSInt | getDataFieldsNumber () const |
| get the number of field used in the operator More... | |
| virtual tBoolean | getDataField (const tUSInt &index, tString &dataName, tUIndex &n, tDimension &dim, const float *&values) const |
| get the data field at index for saving data in vtk,txt,... files. More... | |
| virtual tBoolean | getDataField (const tUSInt &index, tString &dataName, tUIndex &n, tDimension &dim, const double *&values) const |
| get the data field at index for saving data in vtk,txt,... files. More... | |
| virtual tBoolean | getDataField (const tUSInt &index, tString &dataName, tUIndex &n, tDimension &dim, const long double *&values) const |
| get the data field at index for saving data in vtk,txt,... files. More... | |
| virtual tBoolean | isAffine () const |
| return true if the operator is either constant or linear More... | |
| virtual tBoolean | isGradientComputationable () const |
| return true if the gradient of the magnetic excitation is computationable More... | |
| void | setDisplacement (const EMM_RealField &u) |
| set the displacement field More... | |
| void | setDisplacement (const tReal &Ux, const tReal &Uy, const tReal &Uz) |
| set the displacement field to an uniform vector defied on points More... | |
| EMM_RealField & | getDisplacement () |
| get the displacement for writing More... | |
| const EMM_RealField & | getDisplacement () const |
| get the displacement for reading More... | |
| const EMM_RealField & | getDisplacement (const tReal &t) const |
| get the veolicty at time More... | |
| void | setVelocity (const EMM_RealField &v) |
| set the velocity of dicplacement defined on points More... | |
| void | setVelocity (const tReal &Vx, const tReal &Vy, const tReal &Vz) |
| set the displacement velocity field to an uniform vector defined on points More... | |
| EMM_RealField & | getVelocity () |
| get the velocity for writing More... | |
| const EMM_RealField & | getVelocity (const tReal &t) const |
| get the velocity at time More... | |
| const EMM_RealField & | getVelocity () const |
| get the velocity at t for reading More... | |
| EMM_RealField & | getAccelerator () |
| get the accelerator for writing More... | |
| const EMM_RealField & | getAccelerator () const |
| get the accelerator for reading More... | |
| virtual void | setSolver (const tString &solverName) |
| set the solver More... | |
| void | setSolver (SP::MATH_Solver solver) |
| set the solver More... | |
| MATH_Solver * | getSolver () |
| get the solver of the system More... | |
| void | setElasticityState (const tFlag &v) |
| set the elasticity state More... | |
| tBoolean | isSteadyState () const |
| tBoolean | isEquilibriumState () const |
| tBoolean | isFrozenState () const |
| void | setTimeIntegrationMethod (const tFlag &m) |
| set the time integration method for new field More... | |
| const tFlag & | getTimeIntegrationMethod () const |
| get the time integration method for next time step More... | |
| void | setTimeIntegrationOrder (const tInt &o) |
| set the time integration order for new field More... | |
| const tUCInt & | getTimeIntegrationOrder () const |
| get the time integration order for new field More... | |
| const tReal & | getTimeStep () const |
| get the time step for elasticty More... | |
| void | setCFL (const tReal &cfl) |
| set the cfl for computing the initial time step More... | |
| virtual tBoolean | computeFieldsAtTime (const tReal &t, const tFlag &order, const EMM_RealArray &sigma, const EMM_RealField &dM_dt0, const EMM_RealField &M0) |
| compute the fields of operator at time More... | |
| virtual tBoolean | updateAtNextTimeStep (const tReal &dt, const EMM_RealArray &sigma, const EMM_RealField &Mt) |
| update the data of operator at next time step More... | |
| virtual SP::EMM_BlockEquilibriumMatrix | NewEquilibriumMatrix () const |
| create the equilibrium matrix More... | |
| void | setIsEquilibriumMatrixReconditioned (const tBoolean &c) |
| set to true if the equilibrium matrix is conditioned More... | |
| const tBoolean & | isEquilibriumMatrixReconditioned () const |
| get if the equilibrium matrix is conditioned More... | |
| tBoolean | computeEquilibriumState (const EMM_RealArray &sigma, const EMM_RealField &M, const EMM_RealField &U0, EMM_RealField &U) |
compute the equilibirum state 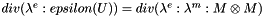 More... More... | |
| virtual void | computeElasticStressMatrixProduct (const tUIndex &nData, const tDimension &dim, const tReal *U, tReal *D) const |
compute the elastic stress Matrix product 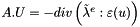 More... More... | |
| virtual void | computeElasticTensor (const EMM_RealField &U, EMM_2PackedSymmetricTensors &eTensor) |
compute the elastic tensor for all cells 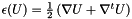 More... More... | |
| void | computeStress (const EMM_RealArray &sigma, const EMM_RealField &U, const EMM_RealField &M, EMM_RealField &stress) const |
compute the stress 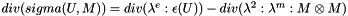 More... More... | |
| virtual void | computeElasticStress (const EMM_RealField &U, EMM_RealField &S) const |
compute the elastic stress for all cells 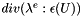 More... More... | |
| void | computeElasticStress (const tUIndex &nData, const tDimension &dim, const tReal *U, tReal *D) const |
compute the elastic stress 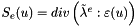 More... More... | |
| void | computeMagneticStress (const EMM_RealArray &sigma, const EMM_RealField &M, EMM_RealField &S) const |
compute the magnetic stress for all cells 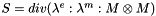 More... More... | |
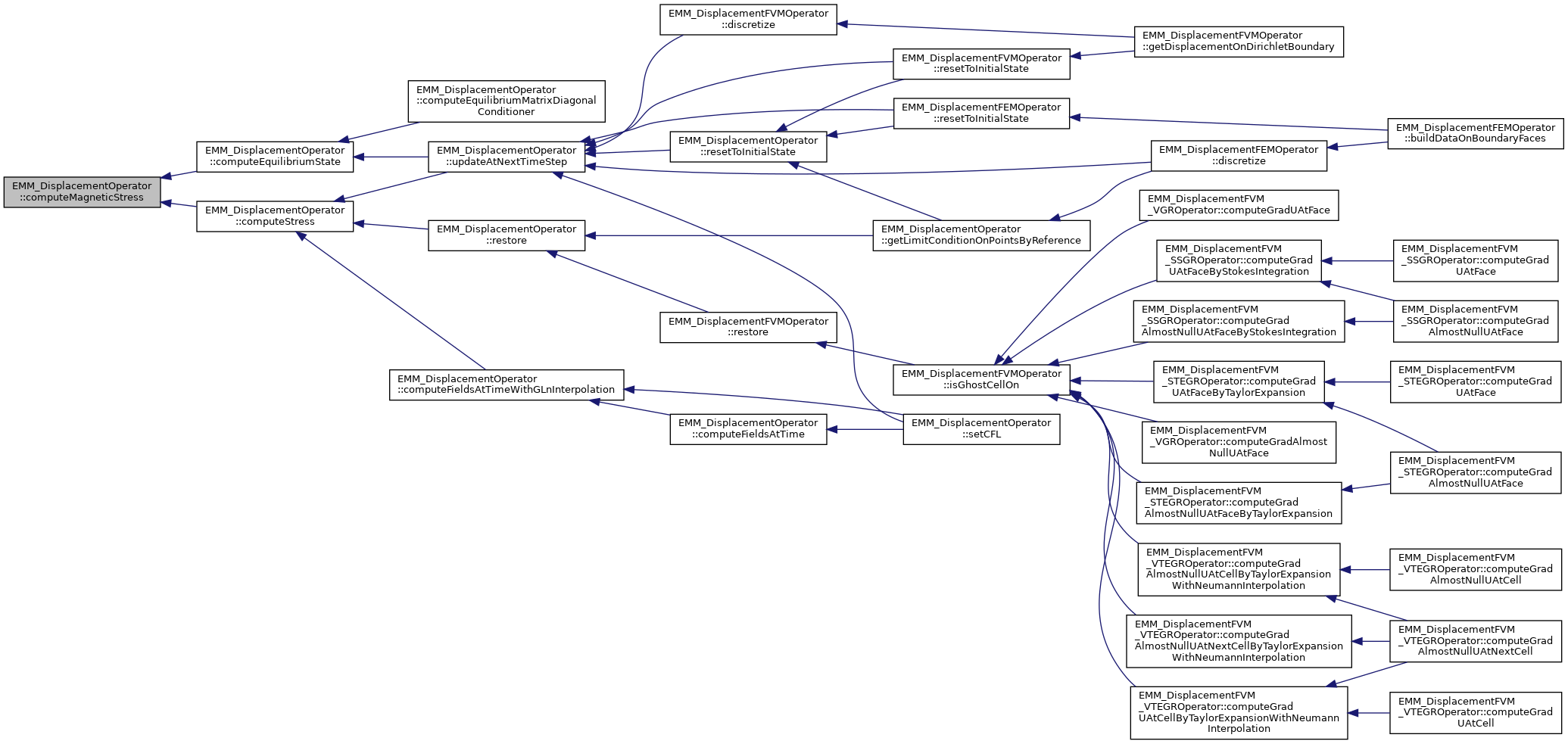
| virtual void | computeMagneticStress (const tReal &alpha, const tReal &beta, const EMM_RealArray &sigma, const EMM_RealField &M, EMM_RealField &S) const =0 |
compute the magnetic stress for all cells from the stress 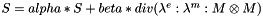 More... More... | |
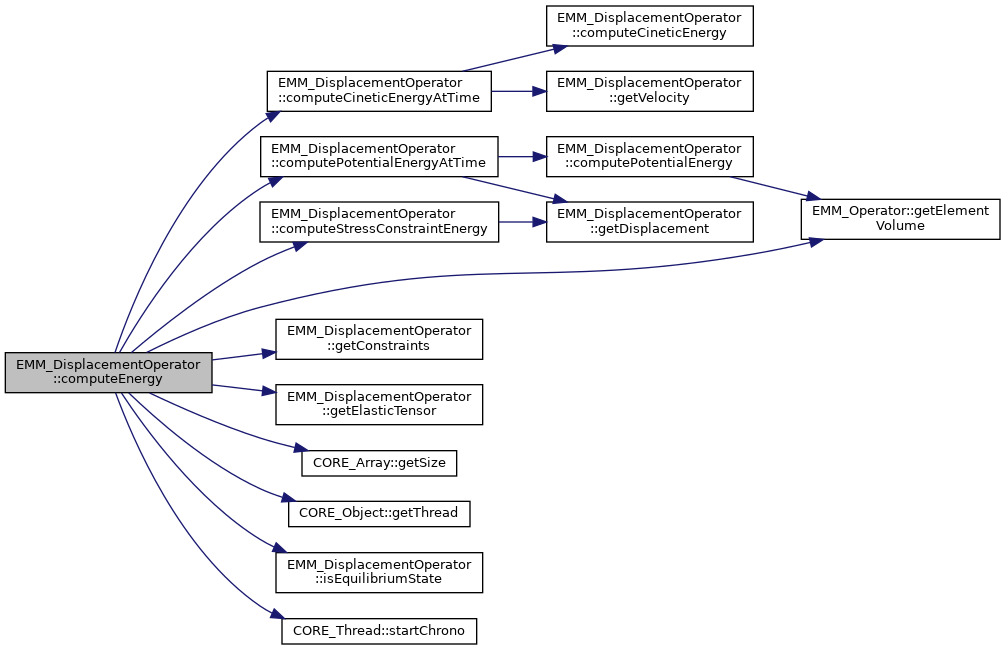
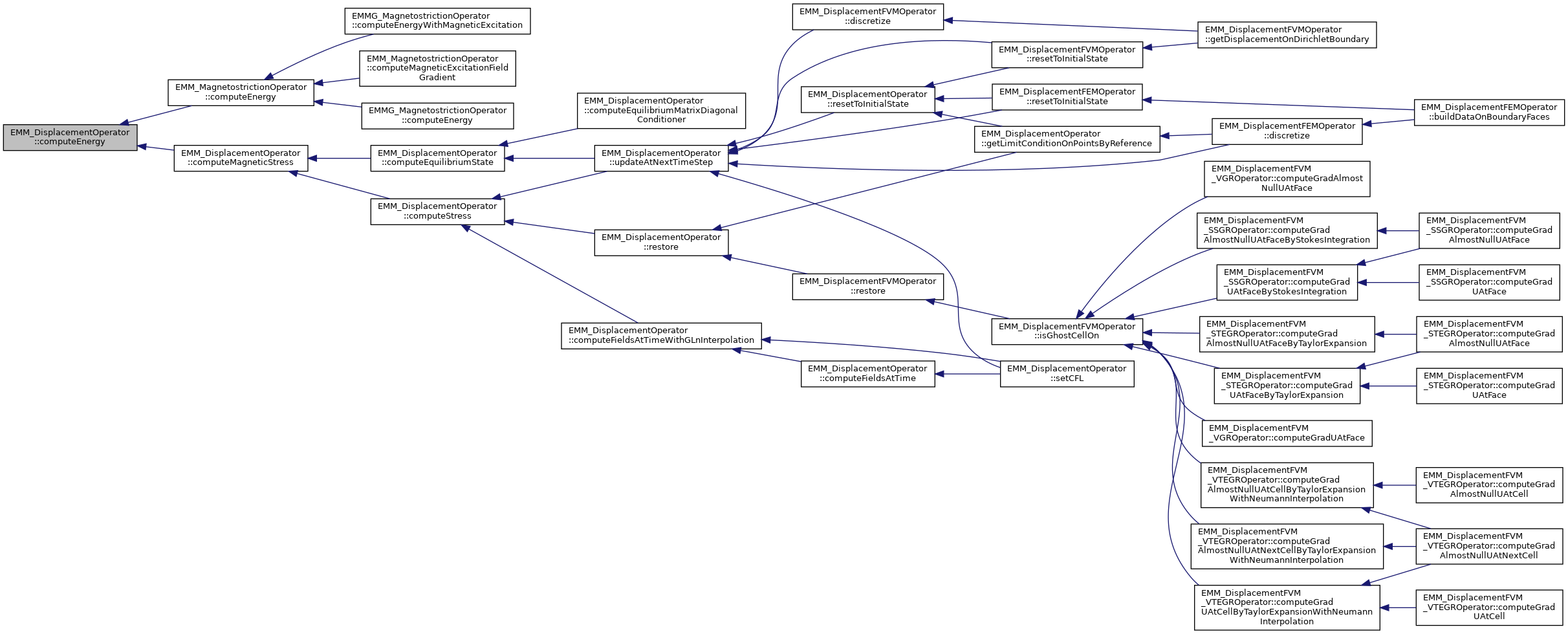
| tReal | computeEnergy (const tReal &t, const tUIndex &nCells, const tDimension &dim, const EMM_RealArray &sigma, const tReal *M) const |
| compute the energy of the magnetostriction operator at current displacement and velocity More... | |
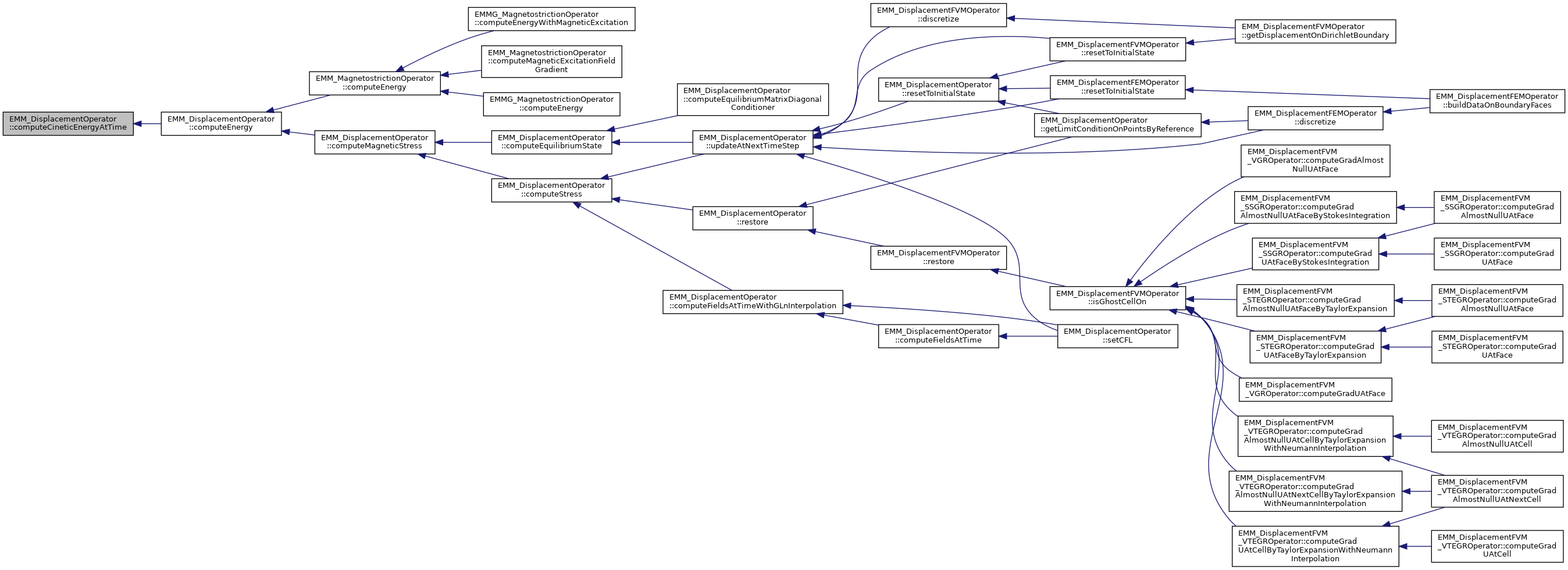
| tReal | computeCineticEnergyAtTime (const tReal &t) const |
| compute the energy due to velocity More... | |
| tReal | computePotentialEnergyAtTime (const tReal &t) const |
| compute the potential energy to the space variation of the displacement More... | |
| tReal | computeStressConstraintEnergy (const tReal &t) const |
| compute the energy of the boundary stress constraint More... | |
| virtual tString | getName () const |
| return an human reading name of the operator More... | |
| const tBoolean & | isCubicVolume () const |
| return the true if the element is cubic More... | |
| const tReal & | getElementVolume () const |
| return the adimensionized volume of the element More... | |
| void | getSharedPointer (SP::CORE_Object &p) |
| get the shared pointer of this class into p More... | |
| void | getSharedPointer (SPC::CORE_Object &p) const |
| get the shared pointer of this class into p More... | |
| tString | getClassName () const |
| return the class name of the object More... | |
| tString | getIdentityString () const |
| return the identity string of the object of the form className_at_address More... | |
| tString | getPointerAddress () const |
| return the identity string of the object More... | |
| template<class T > | |
| tBoolean | isInstanceOf () const |
| test if the clas T is an instance of this class More... | |
| tBoolean | isInstanceOf (const tString &name) const |
| test if the object is an instance of className More... | |
Static Public Member Functions | |
| static void | setIsMemoryChecked (const tBoolean &v) |
| set if the memory checking is used More... | |
| static void | setOut (SP::CORE_Out out) |
| set the output stream More... | |
| static void | resetOut () |
| reset the output stream More... | |
| static void | setThread (SP::CORE_Thread thread) |
| set the thread More... | |
| static void | resetThread () |
| reset the output stream More... | |
| static CORE_Out & | out () |
| get the output More... | |
| static SP::CORE_Out | getOut () |
| get the output More... | |
| static CORE_Thread & | getThread () |
| get the profilier More... | |
| static const tBoolean & | isMemoryChecked () |
| get if the memory checking is used More... | |
| static tString | getClassName (const tString &identityString) |
| return the class name of the object More... | |
| template<class T > | |
| static tString | getTypeName () |
| get type name More... | |
| static tBoolean | is64Architecture () |
| return true if the machine is a 64 bits machine More... | |
| static tBoolean | is32Architecture () |
| return true if the machine is a 32 bits machine More... | |
| static tString | pointer2String (const void *obj) |
| return the string representation of a pointer More... | |
| static void | printObjectsInMemory (ostream &f) |
| print object in memory More... | |
| static void | printObjectsInMemory () |
| print object in memory in the standart output More... | |
| static tChar | getMaxChar () |
| get the max value for tChar type More... | |
| static tChar | getMinChar () |
| get the min value for tChar type More... | |
| static tUChar | getMaxUChar () |
| get the max value for tUChar type More... | |
| static tUChar | getMinUChar () |
| get the min value for tUChar type More... | |
| static tSInt | getMaxSInt () |
| get the max value for tSInt type More... | |
| static tSInt | getMinSInt () |
| get the min value for tSInt type More... | |
| static tUSInt | getMaxUSInt () |
| get the max value for tUSInt type More... | |
| static tUSInt | getMinUSInt () |
| get the min value for tUSInt type More... | |
| static tInt | getMaxInt () |
| get the max value for tInt type More... | |
| static tInt | getMinInt () |
| get the min value for tInt type More... | |
| static tUInt | getMaxUInt () |
| get the max value for tUInt type More... | |
| static tUInt | getMinUInt () |
| get the min value for tUInt type More... | |
| static tLInt | getMaxLInt () |
| get the max value for tLInt type More... | |
| static tLInt | getMinLInt () |
| get the min value for tLInt type More... | |
| static tULInt | getMaxULInt () |
| get the max value for tULInt type More... | |
| static tULInt | getMinULInt () |
| get the min value for tULInt type More... | |
| static tLLInt | getMaxLLInt () |
| get the max value for tULInt type More... | |
| static tLLInt | getMinLLInt () |
| get the min value for tLLInt type More... | |
| static tULLInt | getMaxULLInt () |
| get the max value for tULLInt type More... | |
| static tULLInt | getMinULLInt () |
| get the min value for tULLInt type More... | |
| static tFloat | getMaxFloat () |
| get the max value for tFloat type More... | |
| static tFloat | getMinFloat () |
| get the min value for tFloat type More... | |
| template<class T > | |
| static T | getEpsilon () |
| get the epsilon value for T type More... | |
| template<class T > | |
| static T | getInfinity () |
| get the infinity for T type More... | |
| static tFloat | getFloatEpsilon () |
| get the epsilon value for tFloat type More... | |
| static tFloat | getFloatInfinity () |
| get the infinity value for tFloat type More... | |
| static tDouble | getMaxDouble () |
| get the max value for tDouble type More... | |
| static tDouble | getMinDouble () |
| get the min value for tDouble type More... | |
| static tDouble | getDoubleInfinity () |
| get the infinity value for tFloat type More... | |
| static tDouble | getDoubleEpsilon () |
| get the epsilon value for tDouble type More... | |
| static tLDouble | getMinLDouble () |
| get the min value for tLDouble type More... | |
| static tLDouble | getMaxLDouble () |
| get the max value for tLDouble type More... | |
| static tLDouble | getLDoubleEpsilon () |
| get the epsilon value for tLDouble type More... | |
| static tDouble | getLDoubleInfinity () |
| get the infinity value for tDouble type More... | |
| static tIndex | getMaxIndex () |
| get the max value for the array/vector indexing type More... | |
| static tIndex | getMinIndex () |
| get the min value for the array/vector indexing type More... | |
| static tUIndex | getMaxUIndex () |
| get the max value for difference the array/vector indexing type More... | |
| static tUIndex | getMinUIndex () |
| get the min value for difference the array/vector indexing type More... | |
| static tFlag | getMaxFlag () |
| get the max value for the tFlag type More... | |
| static tFlag | getMinFlag () |
| get the min value for the tFlag type More... | |
| static tUInteger | getMaxUInteger () |
| get the max value for the unsigned integer type More... | |
| static tUInteger | getMinUInteger () |
| get the min value for the unsigned integer type More... | |
| static tInteger | getMaxInteger () |
| get the max value for the integer type More... | |
| static tInteger | getMinInteger () |
| get the min value for the integer type More... | |
| static tReal | getMaxReal () |
| get the max value for the real type More... | |
| static tReal | getMinReal () |
| get the min value for the real type More... | |
| static tReal | getRealEpsilon () |
| get the eps which is the difference between 1 and the least value greater than 1 that is representable. More... | |
| static tReal | getRealInfinity () |
| get the infinity value More... | |
| template<class T > | |
| static T | computeEpsilon () |
| compute epsilon More... | |
Static Public Attributes | |
| static const tFlag | CANONICAL_MASS_MATRIX =0 |
| mass matrix whose each element is real More... | |
| static const tFlag | BLOCK_MASS_MATRIX =1 |
| mass matrix whose each element is a digonal matrixof size 3 More... | |
| static const tFlag | CONDENSED_MASS_MATRIX =2 |
| mass matrix is diagonal More... | |
| static const tFlag | P1 =1 |
| static const tFlag | TE =0 |
| static const tFlag | FROZEN_STATE =1 |
| static const tFlag | EQUILIBRIUM_STATE =3 |
| static const tFlag | UNSTEADY_STATE =0 |
| static const tReal | Mu0 =4*M_PI*1e-07 |
| static const tReal | Gamma =-1.7e11 |
| static const tDimension | X =0 |
| static const tDimension | Y =1 |
| static const tDimension | Z =2 |
| static const tReal | NULL_VALUE [] ={0,0,0} |
Protected Member Functions | |
| EMM_DisplacementFEMOperator (void) | |
| create More... | |
| virtual | ~EMM_DisplacementFEMOperator (void) |
| destroy More... | |
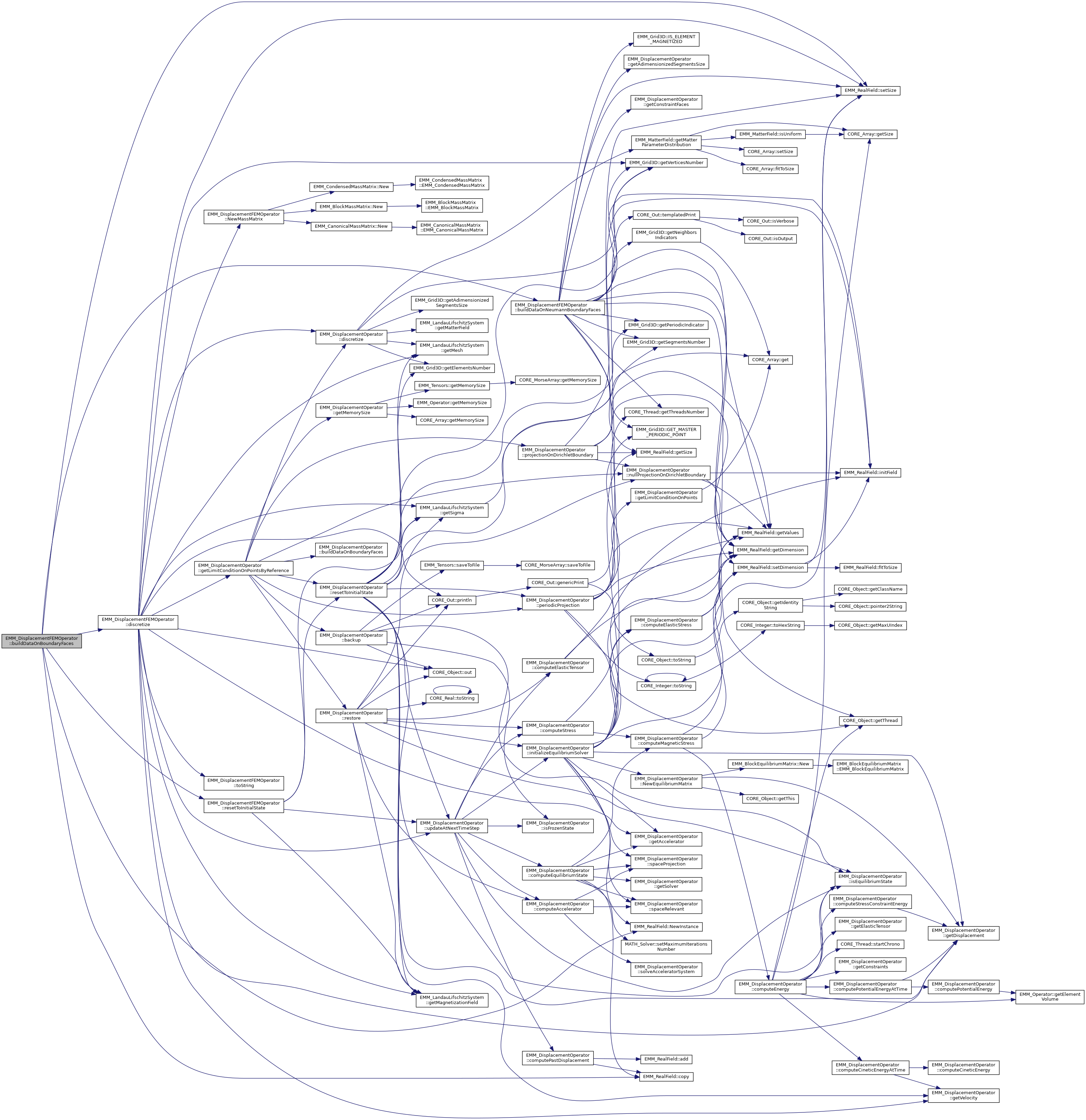
| virtual void | buildDataOnBoundaryFaces (const EMM_Grid3D &mesh, const EMM_LimitConditionArray &limitConditionOnPoints, const EMM_RealField &U0, EMM_RealField &DnU0) |
| build the data on boundary faces More... | |
| virtual tBoolean | solveAcceleratorSystem (EMM_RealField &V) |
| solve the velocity form the accelerator matrix : M.X=V V:=X More... | |
| virtual void | spaceProjection (EMM_RealField &V) const |
| make the projection of the vector B into the solving linear space More... | |
| virtual void | spaceProjection (const EMM_RealField &V0, EMM_RealField &V) const |
| make the projection of the vector B into the solving linear space More... | |
| virtual void | spaceRelevant (EMM_RealField &V) const |
| make the rebuild of the vector V from the solving space. More... | |
| virtual void | computeElasticTensor (const tUIndex &nData, const tDimension &dim, const tReal *U, EMM_2PackedSymmetricTensors &eTensor) const |
| compute the elastic tensor for all cells More... | |
| virtual void | computeElasticStress (const tBoolean &withConstraints, const tReal &beta, const tUIndex &nData, const tDimension &dim, const tReal *U, tReal *D) const |
compute the elastic stress 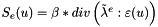 More... More... | |
| virtual void | computeMagneticStress (const tReal &alpha, const tReal &beta, const tUIndex &nCells, const tDimension &dim, const EMM_RealArray &sigma, const tReal *M, const tUIndex &nData, tReal *D) const |
compute the magnetic stress 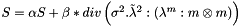 to elastic stress S More... to elastic stress S More... | |
| virtual void | toDoAfterThisSetting () |
| method called after the setting of the shared pointer this method can only be called once. More... | |
| virtual void | initializeEquilibriumSolver (const EMM_RealField &U0) |
| initialize the equilibrium solver More... | |
| void | setThis (SP::CORE_Object p) |
| set this weak shared pointer called toDoAfterThis setting method More... | |
Private Member Functions | |
| SP_OBJECT (EMM_DisplacementFEMOperator) | |
| tBoolean | buildDataOnNeumannBoundaryFaces (const EMM_Grid3D &mesh, const EMM_LimitConditionArray &limitConditionOnPoints, const EMM_RealField &DnU0, EMM_RealField &C) const |
| build the data on boundary faces More... | |
| void | addBoundaryElasticStress (const tReal &beta, const tUIndex &nPoints, const tDimension &dim, tReal *D) const |
| add the elastic stress from boundary More... | |
Private Attributes | |
| tFlag | mMassMatrixType |
| SP::EMM_MassMatrix | mMassMatrix |
Static Private Attributes | |
| static const tCInt | INT_GRAD_PHI [] |
| static const tUCInt | INT_GRAD_PHI_FACTOR =4 |
Detailed Description
This class describes the displacement operator defined on the points of the mesh.
It solves the adimensionzed equations by finite element method:
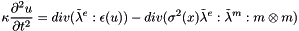
with
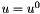 on dirichlet points and
on dirichlet points and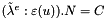 on Neuman points
on Neuman points
To compute the normalized displacement 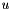 , we multiply by an arbitrary function
, we multiply by an arbitrary function 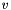 the conservation of momentum normalized equation and by integrating in the whole normalized domain and after using the green formula, for dirichlet problem v
the conservation of momentum normalized equation and by integrating in the whole normalized domain and after using the green formula, for dirichlet problem v 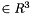 where v=0 on
where v=0 on 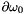 , we obtain by taking into account the Neumann condition on
, we obtain by taking into account the Neumann condition on 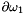 ,
, 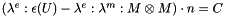
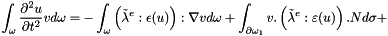
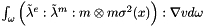
With the applied forces, it becomes:
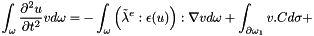
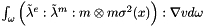
The 3d-variable ![$ u(t,x)=[u_0(t,x),u_1(t,x),u_2(t,x)] $](form_545.png) is decomposed in
is decomposed in 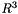 with
with 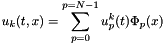 where N is the number of points of the mesh of the magnetized domain,
where N is the number of points of the mesh of the magnetized domain, 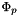 is the Q1 base element :
is the Q1 base element : 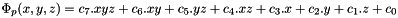 which is null in all the mesh points except at the point p where its value is 1.
which is null in all the mesh points except at the point p where its value is 1.
The points of the mesh is composed by
- a set of interior points denoted by I
- a set of Neumann points denoted by
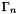
- a set of Dirichlet points denoted by
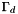
- a set of periodical points
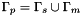 where
where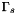 is the set of slave periodical points
is the set of slave periodical points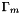 is the set of master periodical points :
is the set of master periodical points : 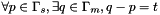 where t is the periodicity
where t is the periodicity
- the set of all points
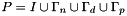
We can have a Dirichlet condition on periodical faces : 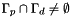 .
.
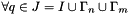 , on all free points, we take
, on all free points, we take 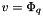 , the k-coordinate projection, we have (as
, the k-coordinate projection, we have (as 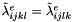 ):
):
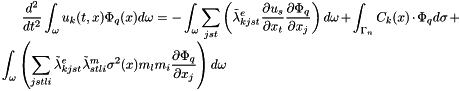
The magnetized domain is discretized with M parallelepiped cells, 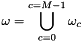 ,
, 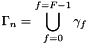 .
.
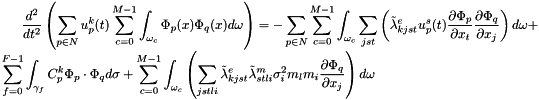
On the discretized domain, we obtain the system , 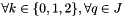 :
:
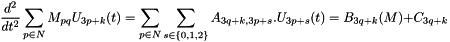 where
where
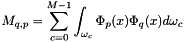 see EMM_MassMatrix::product()
see EMM_MassMatrix::product()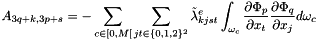 see EMM_DisplacementFEMOperator::computeElasticStress()
see EMM_DisplacementFEMOperator::computeElasticStress()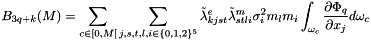 see EMM_DisplacementFEMOperator::computeMagneticStress()
see EMM_DisplacementFEMOperator::computeMagneticStress()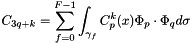 see EMM_DisplacementFEMOperator::addBoundaryElasticStress() called in EMM_DisplacementFEMOperator::computeMagneticStress()
see EMM_DisplacementFEMOperator::addBoundaryElasticStress() called in EMM_DisplacementFEMOperator::computeMagneticStress()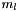 is the mean value of the magnetism at cell
is the mean value of the magnetism at cell 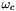
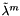 is the value of the variable taken at the cells
is the value of the variable taken at the cells 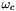 which contains point p and/or q
which contains point p and/or q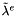 is the value of the variable taken at the cells
is the value of the variable taken at the cells 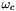 which contains point p and/or q
which contains point p and/or q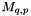 is a matrix of size |J| x |N|
is a matrix of size |J| x |N|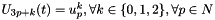 of size 3.|N|
of size 3.|N|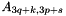 is a matrix of size 3|J| x 3|N|, s in [0,3[
is a matrix of size 3|J| x 3|N|, s in [0,3[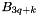 is a vector of size 3.|J| ,
is a vector of size 3.|J| , 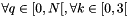
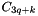 is a vector of size 3.|J| ,
is a vector of size 3.|J| , 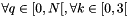
So we have:
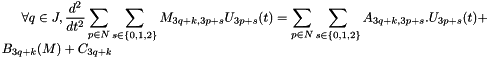
where M_{p,q} is defined by a mass block matrix whose block is 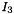 :
:
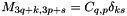 with
with 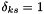 if and only if
if and only if 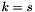 .
.
The linear equation to solve is :
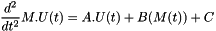
The time step scheme is given by a taylor expansion of order 2 with time step 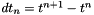 and with
and with 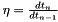
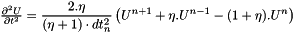
we solve the linear system : 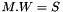 where
where 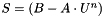
and we deduce the new value of the displacment field thanks to W :
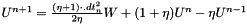 .
.
This formulation leads to a non squared matrix. In order to inverse rapidly the matrix M , the matrix is turned into a symmetric definite positive squared matrix by adding diagonal rows on linked points in 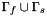 :
:
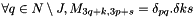 and
and
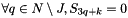
to ensure that 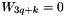 after resolving the linear system.
after resolving the linear system.
Then U is rebuild by the formulas :
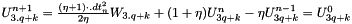 , for Dirichlet points q
, for Dirichlet points q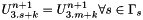 and m is the associated periodical point in
and m is the associated periodical point in 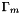 .
.
So to solve the U we use the following algorithm:
- compute the S vector of size 3.|N|
- make a projection of S on the solving space
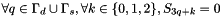
- solve the system of size |N|^2,
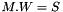 by the gradient conjugate method. Note that only the Matrix Vector product needs to be implemented.
by the gradient conjugate method. Note that only the Matrix Vector product needs to be implemented. - rebuild the vector W from the solving space
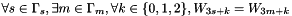 .
. - compute U from W by the formula
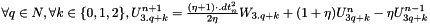 .
.
Note that if we have a Dirichlet condition depending on time (not implemented yet), the projection of S of the solving space will impose to set :
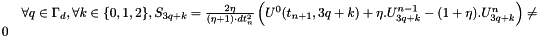
To reduce the size of the system, a map from N into J may be built but it will need more memory size to store the map and it is not sure that a lot of CPU time may be saved (not implemented).
To compute the equilibrium state we have to solve the equations : 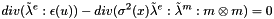
with
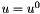 on dirichlet points and
on dirichlet points and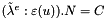 on Neuman points
on Neuman points
The weak formulation gives :
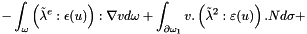
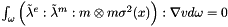
In order to ensure the definite positive of the operator, we put it in the form : 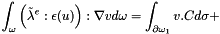
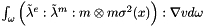
The discrete formulation is
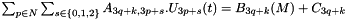 where
where
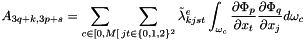 see EMM_DisplacementFEMOperator::computeElasticStress()
see EMM_DisplacementFEMOperator::computeElasticStress()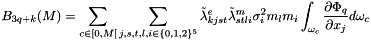 see EMM_DisplacementFEMOperator::computeMagneticStress()
see EMM_DisplacementFEMOperator::computeMagneticStress()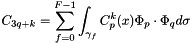 see EMM_DisplacementFEMOperator::addBoundaryElasticStress() called in EMM_DisplacementFEMOperator::computeMagneticStress()
see EMM_DisplacementFEMOperator::addBoundaryElasticStress() called in EMM_DisplacementFEMOperator::computeMagneticStress()
To compute 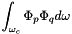 ,
, 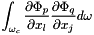 or
or 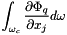 ,
, 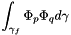 , each cell
, each cell 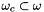 and each
and each 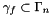 of the mesh is transformed into the referenced cell in
of the mesh is transformed into the referenced cell in ![$ [0,1]\times[0,1]\times[0,1]$](form_616.png) with reference nodes
with reference nodes 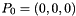 ,
, 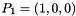 ,
, 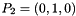 ,
, 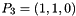 ,
, 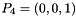 ,
, 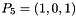 ,
, 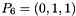 ,
, 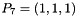 by the transform function
by the transform function 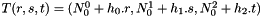 where
where ![$ r,s,t \in [0,1]^3=\hat{\omega} $](form_626.png) ,
, 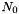 if the base corner (min point) of the mesh cell
if the base corner (min point) of the mesh cell 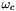 , and
, and 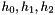 , the size of the cell mesh
, the size of the cell mesh 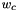 .
.
The corresponding reference base function 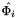 on the cell 's point
on the cell 's point 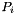 is given by
is given by 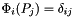 .
.
The integral is transformed into a referenced cell: 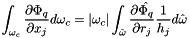 where
where 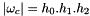 by normalization.
by normalization.
The computation 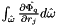 is done as follow:
is done as follow:
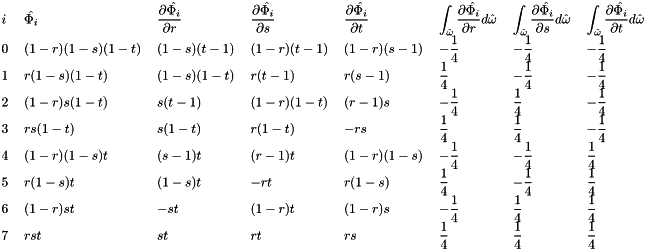
We can compress formula by 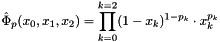 where
where 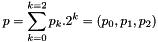 , base point of the reference element.
, base point of the reference element.
Then we have 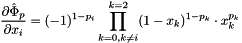 .
.
So we have 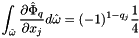 with
with 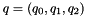
It can be rewritten as 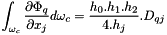 where D is the matrix 8x3:
where D is the matrix 8x3:

To compute the following integrals, we note that :
So, 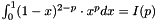 where
where
So 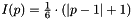
So to compute 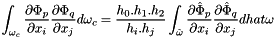 .
.
![$ \forall p,q \in [0,7]^2, \forall i \neq j , \int_{\hat \omega } \frac{\partial \hat \Phi_p}{\partial x_i}\frac{\partial \hat \Phi_q}{\partial x_j} d{\hat \omega} = \displaystyle \frac{1}{6.2.2} \cdot (-1)^{p_i+q_j} \cdot (|p_k+q_k-1|+1) $](form_654.png) , k is the only value in {0,1,2} different from i and j.
, k is the only value in {0,1,2} different from i and j.
![$ \forall p,q \in [0,7]^2, \forall i \int_{\hat \omega } \frac{\partial \hat \Phi_p}{\partial x_i}\frac{\partial \hat \Phi_q}{\partial x_i} d{\hat \omega} = \displaystyle \frac{1}{6.6} \cdot (-1)^{p_i+q_i} \cdot \prod_{k=0,k\neq i}^{k=2} (|p_k+q_k-1|+1) $](form_655.png) .
.
To compute the constraint matrix, 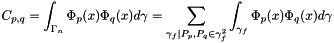
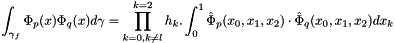 where the normal of the face f is on the l-direction. But,
where the normal of the face f is on the l-direction. But,
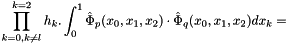
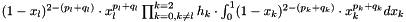 .
.
As we have:
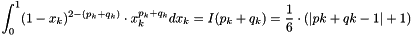
we conclude
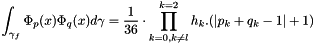
To compute the mass matrix, 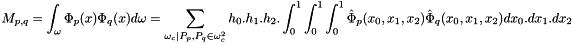
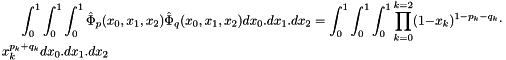
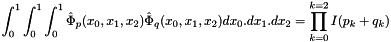
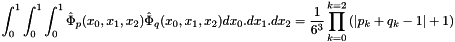
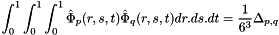
where  is a column packed symmetric matrix matrix 8x8:
is a column packed symmetric matrix matrix 8x8:
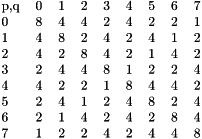
If we use the mean formula of integration 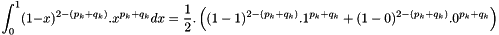 ,
,
we have 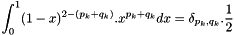 .
.
So 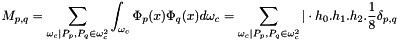 with is a diagonal matrix called Condensed Mass matrix.
with is a diagonal matrix called Condensed Mass matrix.
The K & M matrix are computing during the discretization step because they do not evolutate during the relaxation process.
The normalized energy of this implemented displacement class is reduced to its cinetic energy:
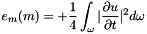
The velocity verifies by using a Taylor expansion of order 2 in time with 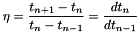
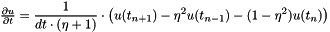
@author Stephane Despreaux @version 1.0
Constructor & Destructor Documentation
◆ EMM_DisplacementFEMOperator()
|
protected |
create
References BLOCK_MASS_MATRIX, and mMassMatrixType.
◆ ~EMM_DisplacementFEMOperator()
|
protectedvirtual |
destroy
Member Function Documentation
◆ addBoundaryElasticStress()
|
private |
add the elastic stress from boundary
- Parameters
-
[in] beta : multiplicator of Boundary Stress B [in] nPoints number of points [in] dim dimension of the problem in [1,3] [in,out] D the elastic stress of size nPoints*dim
D+=beta.B with 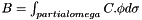
References EMM_DisplacementOperator::getConstraints(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), null, OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tDimension, tReal, tUIndex, and tUInteger.
Referenced by computeElasticStress(), and getDataFieldSpace().

◆ adimensionize()
|
inlinevirtualinherited |
adimensionize the operator
- Parameters
-
[in] Le common elasticity adimensionized parameter [in] Ms common magnetization at saturation [in] T caracterictic time [in] L caracteristic length
adimensionize the associated displacement operator
Reimplemented from EMM_Operator.
◆ backup()
|
virtualinherited |
backup of the operator data into file(s) used for restoring
- Parameters
-
prefix : common prefix of the saving files suffix : common suffix of the saving files ext : common extension of the saving files
- Returns
- true if the saving of the U & V file have succeeded
It saves
- the current time step in {prefix}_dt_{suffix}.{ext}
- U at previous time step in {prefix}_Unm1_{suffix}.{ext}
- U at current time step in {prefix}_Un_{suffix}.{ext}
- V at current time step in {prefix}_Vn_{suffix}.{ext}
- dV/dt at current time step in {prefix}_Acc_{suffx}.{ext}
Reimplemented from EMM_Operator.
Reimplemented in EMM_DisplacementFVMOperator.
References EMM_DisplacementOperator::isEquilibriumState(), EMM_DisplacementOperator::isFrozenState(), EMM_DisplacementOperator::mAccelerator, EMM_DisplacementOperator::mDt, EMM_DisplacementOperator::mEpsilonUt, EMM_DisplacementOperator::mTimeIntegrationMethod, EMM_DisplacementOperator::mUn, EMM_DisplacementOperator::mUnm1, EMM_DisplacementOperator::mVn, CORE_Object::out(), CORE_Out::println(), EMM_Tensors::saveToFile(), tBoolean, EMM_DisplacementOperator::TE, and tString.
Referenced by EMM_DisplacementFVMOperator::backup(), and EMM_DisplacementOperator::getLimitConditionOnPointsByReference().

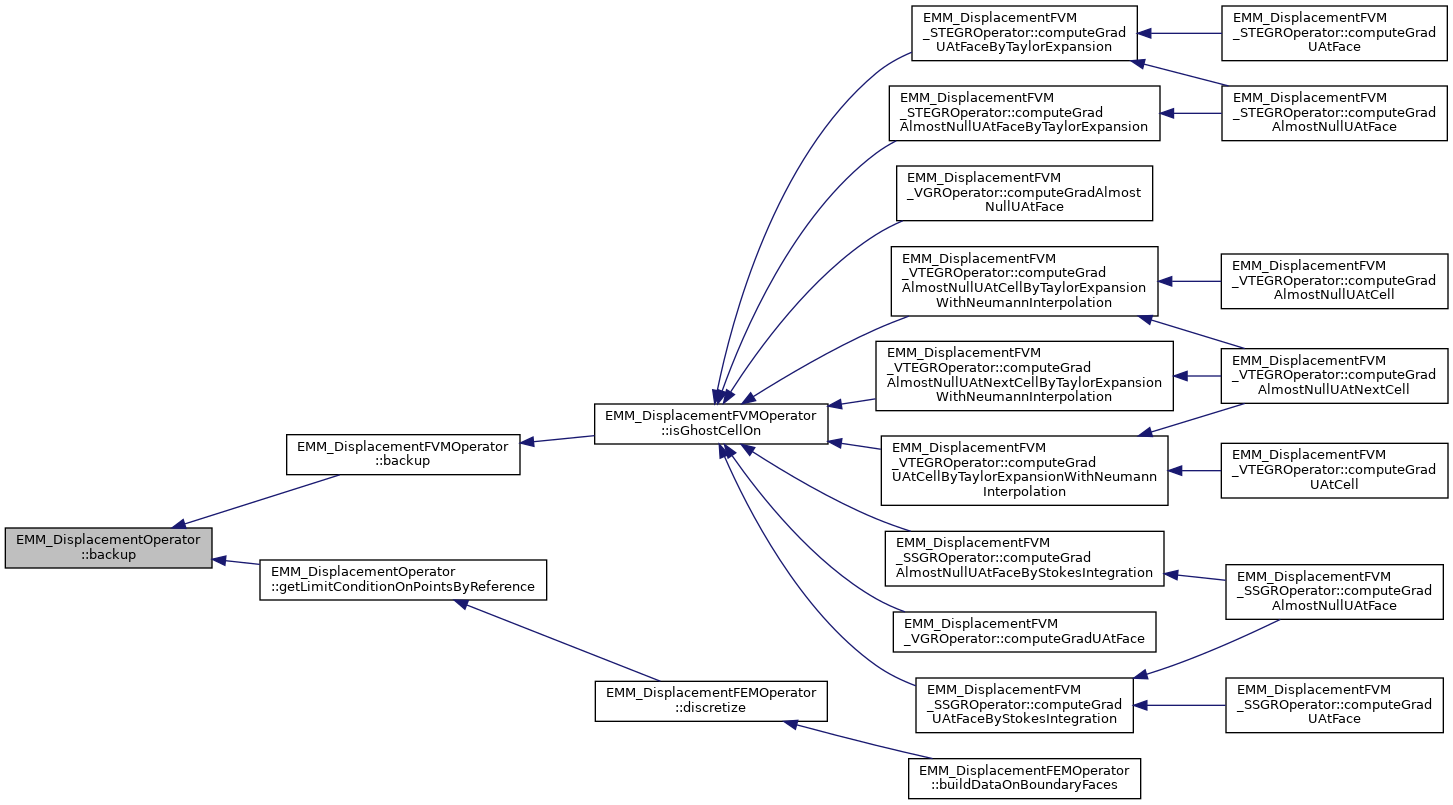
◆ buildDataOnBoundaryFaces()
|
inlineprotectedvirtual |
build the data on boundary faces
- Parameters
-
mesh the mesh of the domain limitConditionOnPoints : limit condition on points U0 : U at all points at t=0 DnU0 : grad UO . N at each point slave Naumann points and Neumann points
recompute the DnUO with the formula :
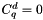 if q is not a Neumann points
if q is not a Neumann points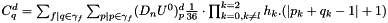 where the l is the direction of the normal to
where the l is the direction of the normal to 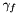
Implements EMM_DisplacementOperator.
References buildDataOnNeumannBoundaryFaces(), EMM_RealField::copy(), discretize(), EMM_RealField::NewInstance(), resetToInitialState(), EMM_RealField::setSize(), and tBoolean.
◆ buildDataOnNeumannBoundaryFaces()
|
private |
build the data on boundary faces
- Parameters
-
mesh the mesh of the domain limitConditionOnPoints : limit condition on points DnU0 : grad UO . N at each point C : the constraint of ach point of the mesh
compute the constraint on each point of the mesh with the formula :
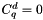 if q is not a Neumann points
if q is not a Neumann points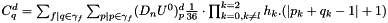 where the l is the dierction of the normal to
where the l is the dierction of the normal to 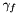
- Returns
- false if U is null
periodicity of the domain
start=iq+Px.(jq+Py.kq)
References EMM_Grid3D::ELEMENT_POINTS, EMM_Grid3D::FACE_POINTS, EMM_Grid3D::GET_MASTER_PERIODIC_POINT(), EMM_DisplacementOperator::getAdimensionizedSegmentsSize(), EMM_DisplacementOperator::getConstraintFaces(), EMM_RealField::getDimension(), EMM_Grid3D::getNeighborsIndicators(), EMM_Grid3D::getPeriodicIndicator(), EMM_Grid3D::getSegmentsNumber(), EMM_RealField::getSize(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), EMM_RealField::getValues(), EMM_Grid3D::getVerticesNumber(), iand, EMM_RealField::initField(), EMM_Grid3D::IS_ELEMENT_MAGNETIZED(), EMM_Grid3D::NEUMANN_LIMIT_CONDITION, null, OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT_REDUCTION, EMM_Grid3D::POINTS_NUMBER_PER_ELEMENT, EMM_Grid3D::POINTS_NUMBER_PER_FACE, EMM_RealField::setDimension(), EMM_RealField::setSize(), EMM_Grid3D::SLAVE_LIMIT_CONDITION, tBoolean, tCellFlag, tDimension, tFlag, tInteger, tLimitCondition, tReal, tUCInt, tUIndex, tUInteger, and tUSInt.
Referenced by buildDataOnBoundaryFaces().
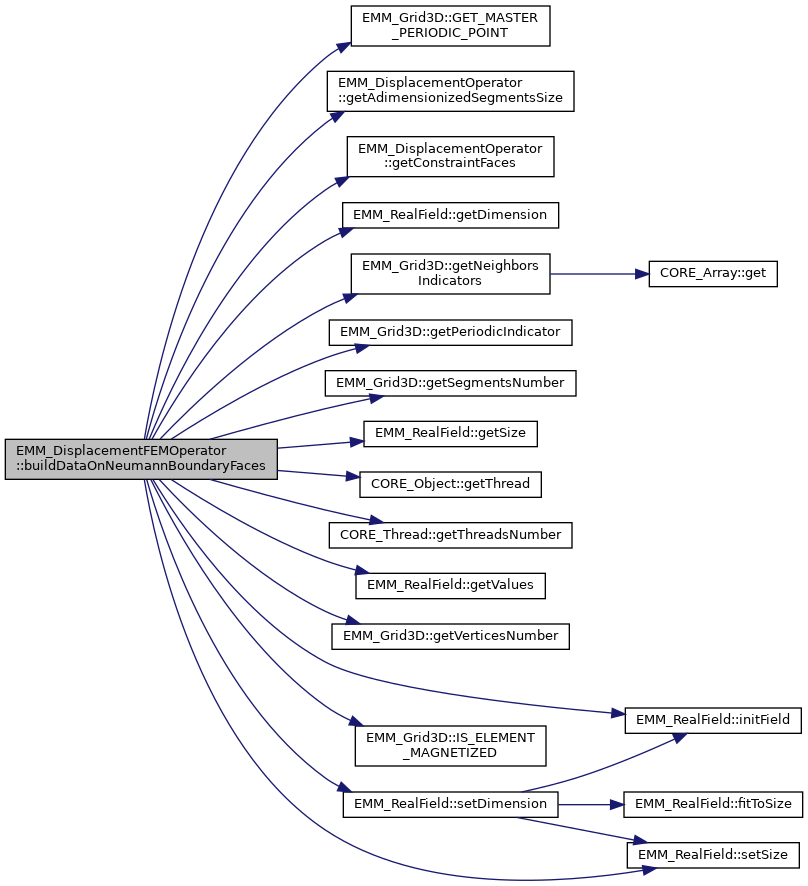

◆ computeCineticEnergy()
|
virtual |
compute the energy of the magnetostriction operator at current displacement and velocity
- Parameters
-
V velocity
- Returns
- cinetic energy value
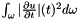
Implements EMM_DisplacementOperator.
References EMM_DisplacementOperator::getAdimensionizedVolumicMass(), EMM_RealField::getSize(), and mMassMatrix.
Referenced by getDataFieldSpace().


◆ computeCineticEnergyAtTime()
compute the energy due to velocity
- Parameters
-
t time in [0,dt[ where dt is the time step
- Returns
- cinetic energy value
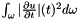
References EMM_DisplacementOperator::computeCineticEnergy(), EMM_DisplacementOperator::getVelocity(), and tReal.
Referenced by EMM_DisplacementOperator::computeEnergy().
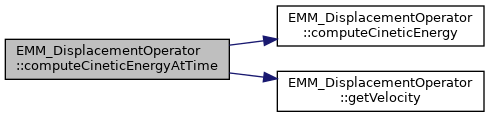
◆ computeElasticStress() [1/3]
|
protectedvirtual |
compute the elastic stress 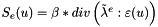
- Parameters
-
withConstraints : if true compute the whore opertaor if false, compute only the linear part of operator beta factor of the strees to turn intto definite positive/negative matrix nData number of data for U (nCells or nVertices depending on the method) dim dimension of the problem in [1,3] U the displacement field values D the elastic stress of size nData*dim
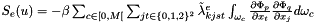
It is an affine operator 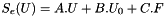 where
where
- A is symmetric definite positive which is the linear part of the affine operator
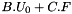 is the constant part of the affine operator
is the constant part of the affine operator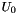 is the Dirichlet values of the field
is the Dirichlet values of the field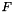 is the applied forces
is the applied forces
start=iq+Px.(jq+Py.kq)
Implements EMM_DisplacementOperator.
References addBoundaryElasticStress(), EMM_Grid3D::DIRICHLET_LIMIT_CONDITION, EMM_Grid3D::ELEMENT_POINTS, EMM_Grid3D::GET_MASTER_PERIODIC_POINT(), EMM_DisplacementOperator::getAdimensionizedSegmentsSize(), EMM_Operator::getElementVolume(), EMM_DisplacementOperator::getLambdaE(), EMM_DisplacementOperator::getLimitConditionOnPoints(), getNeighborsIndicator(), getPeriodicIndicator(), getPointsNumber(), EMM_4Tensors::getTensorSize(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), EMM_Grid3D::IS_ELEMENT_MAGNETIZED(), EMM_Tensors::isNotNull(), null, OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, EMM_Grid3D::POINTS_NUMBER_PER_ELEMENT, EMM_Grid3D::SLAVE_LIMIT_CONDITION, tBoolean, tCellFlag, tDimension, tFlag, tInteger, tLimitCondition, tReal, tUCInt, tUIndex, and tUInteger.
Referenced by EMMG_DisplacementFEMOperator::computeElasticStress(), and getDataFieldSpace().
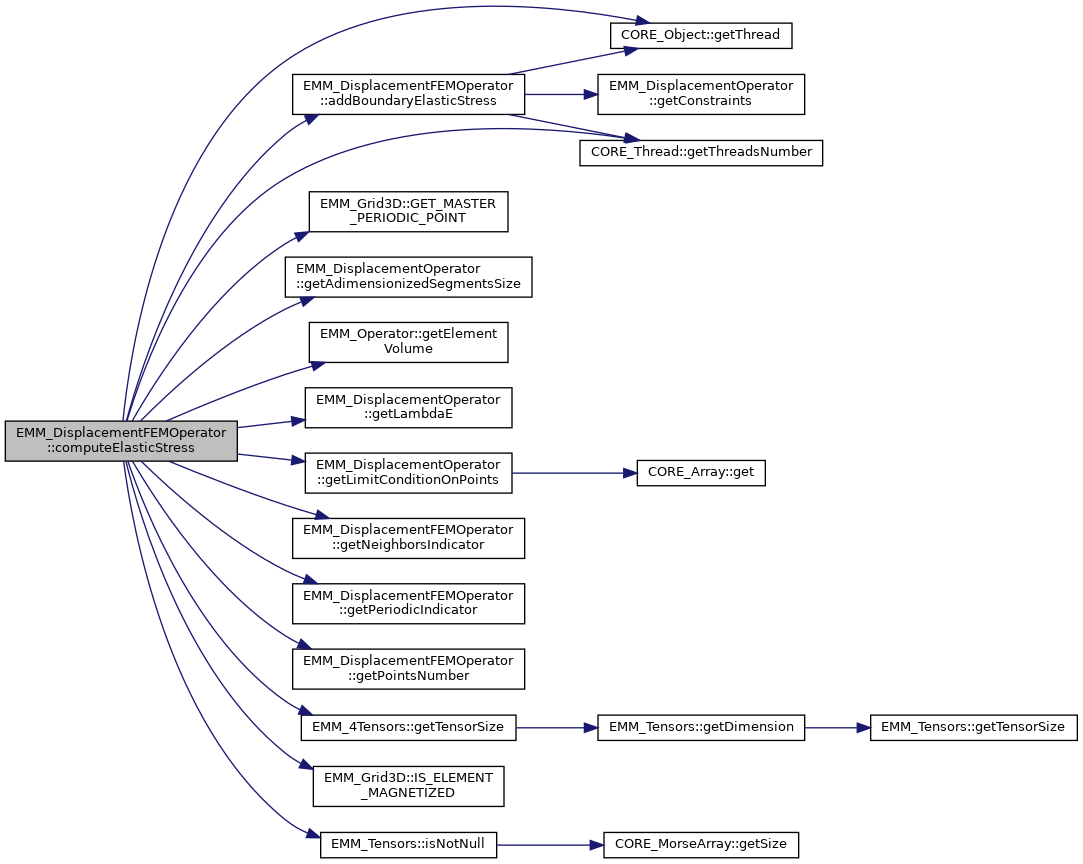
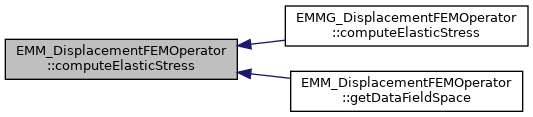
◆ computeElasticStress() [2/3]
|
inlinevirtualinherited |
compute the elastic stress for all cells 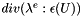
- Parameters
-
U the displacement field S the elastic stress field
It computes:
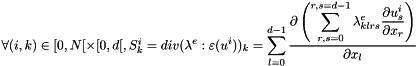 where
where
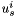 is the s-coordinate of the displacement u at cell i when s is in [0,d[ and d is the dimension of the space (i.e. 3).
is the s-coordinate of the displacement u at cell i when s is in [0,d[ and d is the dimension of the space (i.e. 3).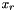 is the r-coordinate of points in cell
is the r-coordinate of points in cell
Reimplemented in EMMG_DisplacementFVM_VOGGROperator, EMMG_DisplacementFVM_SSGROperator, EMMG_DisplacementFVM_STEGROperator, EMMG_DisplacementFVM_VTEGROperator, and EMMG_DisplacementFEMOperator.
References EMM_RealField::getDimension(), EMM_RealField::getValues(), tDimension, tReal, and tUIndex.
Referenced by EMM_DisplacementOperator::computeElasticStress(), EMM_DisplacementOperator::computeElasticStressMatrixProduct(), EMM_DisplacementOperator::computeStress(), and EMM_DisplacementOperator::initializeEquilibriumSolver().


◆ computeElasticStress() [3/3]
|
inlineinherited |
compute the elastic stress 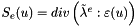
- Parameters
-
nData number of data for U (nCells or nVertices depending on the method) dim dimension of the problem in [1,3] U the displacement field values D the elastic stress of size nData*dim
It computes 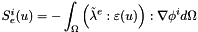
![$ \forall d \in [0,3[, \forall q \in [0,P[, B[3q+d]= \displaystyle - \sum_{c \in V(P_q)} \int_{\omega_c} \sum_{p=0}^{p=8} \sum_{lrs} \left ( \lambda^c_{dlrs} u_{i_P}^s(t)\frac{\partial \Phi_p }{\partial x_r } \frac{\partial \Phi_q }{\partial x_l} \right ) d\omega $](form_980.png)
where 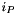 is the index of the p-th point into cell
is the index of the p-th point into cell 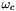 , P is the number of interior magnetized points and
, P is the number of interior magnetized points and 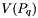 is the set of cells connected to point q.
is the set of cells connected to point q.
Algorithm:
- D=0, initialize to 0
- pts={[0,0,0],[1,0,0],[0,1,0],[1,1,0],[0,0,1],[1,0,1],[0,1,1],[1,1,1]} local coordinates of cell points.
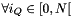
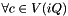
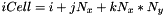 index of the cell c
index of the cell c- if iCell is in magnetized domain
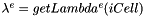 of size 3x3x3x3
of size 3x3x3x3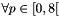 loop on nodes of cell iCell of local coordinate
loop on nodes of cell iCell of local coordinate 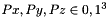 .
.- iP is the global index of local point p
- iP=(i+Px)+Nx*(j+Py)+Nx.Ny.(k+Pz)
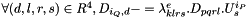 with
with
References EMM_DisplacementOperator::computeElasticStress(), tBoolean, tDimension, tReal, and tUIndex.

◆ computeElasticStressMatrixProduct()
|
inlinevirtualinherited |
compute the elastic stress Matrix product 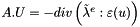
- Parameters
-
nData number of data for U (nCells or nVertices depending on the method) dim dimension of the problem in [1,3] U the displacement field values D the elastic stress of size nData*dim
make the computation of A.U=-S_e.U for the elastic equilibrium matrix product with null constraints
Reimplemented in EMM_DisplacementFVM_VIGROperator.
References EMM_DisplacementOperator::computeElasticStress(), EMM_DisplacementOperator::computeElasticTensor(), tDimension, tReal, and tUIndex.

◆ computeElasticTensor() [1/2]
|
protectedvirtual |
compute the elastic tensor for all cells
- Parameters
-
nData size of the displacement field dim dimension of the displacement field U values of the displacement field eTensor the elastic tensor of size 3x3 stored in column-packed symmetric upper matrix array of size 6
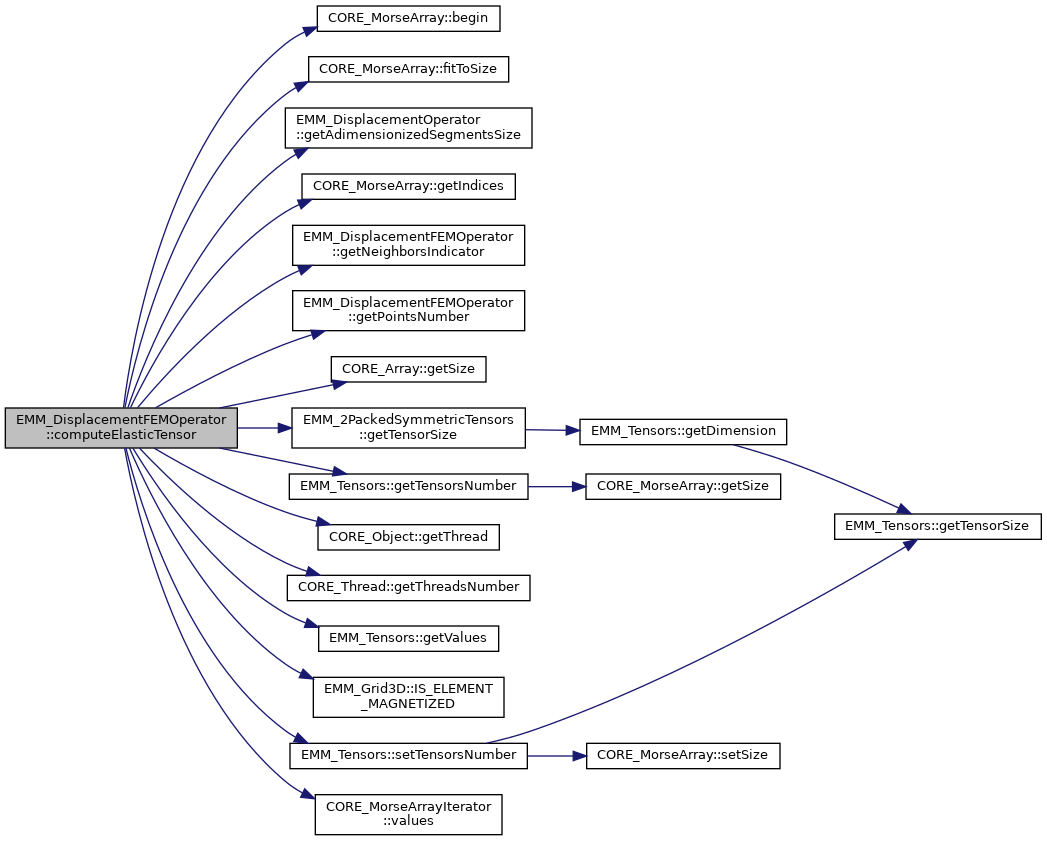
![$ \forall (r,s) \in [0,3[^2, \varepsilon_{rs}= \displaystyle \frac{1}{2}\left ( \frac{\partial u_r}{\partial x_s} + \frac{\partial u_s}{\partial x_r} \right )=eTensor[r+(s*(s+1)/2)]$](form_681.png) where
where
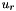 is the r-coordinate of the displacement u
is the r-coordinate of the displacement u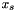 is the s-coordinate of point in cell
is the s-coordinate of point in cell
The finite element approximation of 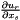 at cell i , is given by
at cell i , is given by
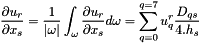 where
where 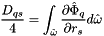
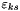 is computed as follow in a packed symmetric column storage at cell i :
is computed as follow in a packed symmetric column storage at cell i :
- for all k in [0,3 [
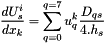
- for all s in [0,k[,
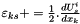
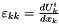
- for all s in ]k,3[,
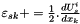
Implements EMM_DisplacementOperator.
References CORE_MorseArray< T >::begin(), EMM_Grid3D::ELEMENT_POINTS, CORE_MorseArray< T >::fitToSize(), EMM_DisplacementOperator::getAdimensionizedSegmentsSize(), CORE_MorseArray< T >::getIndices(), getNeighborsIndicator(), getPointsNumber(), CORE_Array< T >::getSize(), EMM_2PackedSymmetricTensors::getTensorSize(), EMM_Tensors::getTensorsNumber(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), EMM_Tensors::getValues(), INT_GRAD_PHI, INT_GRAD_PHI_FACTOR, EMM_Grid3D::IS_ELEMENT_MAGNETIZED(), OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, EMM_Grid3D::POINTS_NUMBER_PER_ELEMENT, EMM_Tensors::setTensorsNumber(), tBoolean, tCellFlag, tCInt, tDimension, tReal, tUCInt, tUIndex, tUInteger, and CORE_MorseArrayIterator< T >::values().
Referenced by getDataFieldSpace().

◆ computeElasticTensor() [2/2]
|
virtualinherited |
compute the elastic tensor for all cells 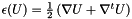
- Parameters
-
U the displacement field eTensor the elastic tensor of size 3x3 stored in row-packed symmetric upper matrix array of size 6
![$ \forall (r,s) \in [0,3[^2, \varepsilon_{rs}= \displaystyle \frac{1}{2}\left ( \frac{\partial u_r}{\partial x_s} + \frac{\partial u_s}{\partial x_r} \right )=eTensor[r+(s*(s+1)/2)]$](form_681.png) where
where
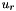 is the r-coordinate of the displacement u
is the r-coordinate of the displacement u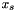 is the s-coordinate of point in cell
is the s-coordinate of point in cell
Reimplemented in EMM_DisplacementFVMOperator, and EMM_DisplacementFVM_VIGROperator.
References EMM_RealField::getDimension(), EMM_RealField::getValues(), tDimension, tReal, and tUIndex.
Referenced by EMM_DisplacementOperator::computeElasticStressMatrixProduct(), EMM_DisplacementFVMOperator::computeElasticTensor(), EMM_DisplacementOperator::computeFieldsAtTime(), EMM_DisplacementOperator::restore(), and EMM_DisplacementOperator::updateAtNextTimeStep().

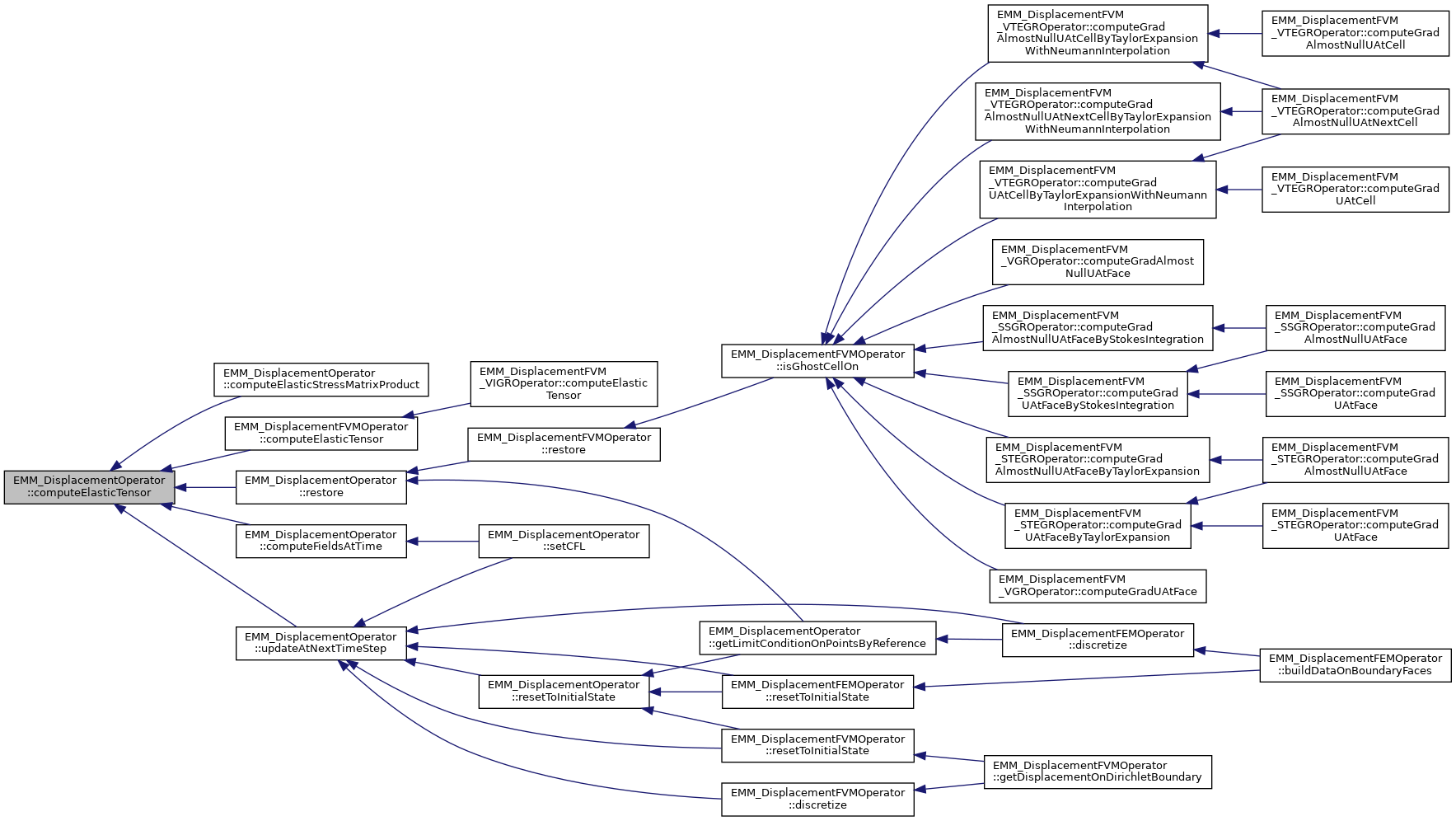
◆ computeEnergy()
|
inherited |
compute the energy of the magnetostriction operator at current displacement and velocity
- Parameters
-
t the time in [0,dt[ where dt is the time step nCells : number of cells dim dimension of each point of mesh sigma the weight of each cell M the magnetization field values
- Returns
- energy value :
![$ E(m,u)=\displaystyle \frac{1}{2} \int_\omega \sigma^4(x)[\tilde \lambda^e:(\tilde \lambda^m:m \otimes m)]:(\tilde \lambda^m:m \otimes m) d\omega $](form_992.png)
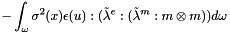
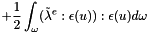
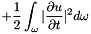
References EMM_DisplacementOperator::computeCineticEnergyAtTime(), EMM_DisplacementOperator::computePotentialEnergyAtTime(), EMM_DisplacementOperator::computeStressConstraintEnergy(), EMM_DisplacementOperator::getConstraints(), EMM_DisplacementOperator::getElasticTensor(), EMM_Operator::getElementVolume(), CORE_Array< T >::getSize(), CORE_Object::getThread(), EMM_DisplacementOperator::isEquilibriumState(), EMM_DisplacementOperator::mLme, CORE_Thread::startChrono(), tBoolean, tReal, and tString.
Referenced by EMM_MagnetostrictionOperator::computeEnergy(), and EMM_DisplacementOperator::computeMagneticStress().
◆ computeEpsilon()
|
inlinestaticinherited |
compute epsilon
- Returns
- the epsilon value eps=10^{-p/3} where p is defined by getEpsilon()=10^{-p}
◆ computeEquilibriumMatrixDiagonalConditioner()
|
virtual |
compute the diagonal conditioner
- Parameters
-
[out] D is the diagonal conditioner of the equilibrium matrix by defualt the diagonal matrix is the identity (its size if set to 0);
start=iq+Px.(jq+Py.kq)
Reimplemented from EMM_DisplacementOperator.
References EMM_Grid3D::DIRICHLET_LIMIT_CONDITION, EMM_Grid3D::ELEMENT_POINTS, EMM_DisplacementOperator::getAdimensionizedSegmentsSize(), EMM_RealField::getDimension(), EMM_DisplacementOperator::getDisplacement(), EMM_Operator::getElementVolume(), EMM_DisplacementOperator::getLambdaE(), EMM_DisplacementOperator::getLimitConditionOnPoints(), getNeighborsIndicator(), getPeriodicIndicator(), getPointsNumber(), EMM_4Tensors::getTensorSize(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), MATH_Vector::getValues(), EMM_Grid3D::IS_ELEMENT_MAGNETIZED(), EMM_DisplacementOperator::isEquilibriumMatrixReconditioned(), EMM_Tensors::isNotNull(), OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, EMM_Grid3D::POINTS_NUMBER_PER_ELEMENT, MATH_Vector::setSize(), EMM_Grid3D::SLAVE_LIMIT_CONDITION, tBoolean, tCellFlag, tDimension, tFlag, tInteger, tLimitCondition, tReal, tUCInt, tUIndex, and tUInteger.
Referenced by getDataFieldSpace().

◆ computeEquilibriumState()
|
inherited |
compute the equilibirum state 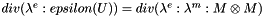
- Parameters
-
[in] sigma : the weight array due to unhomegeneous magnetization at saturation [in] M : the magnetization field [in] U0 : the displacement field at dirichlet point [out] U the dispacement field at equilibrium
- Returns
- true if the solving succeeds
- compute the right hand side of the equation
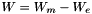
- make a projection of W into f the solving space (W=U0 on Dirichlet point) in order to ensure that U=U_0 on Dirichlet boundary
- solve the linear equation with a conjugate gradient method
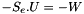 S_e is diagonla for derichlet point
S_e is diagonla for derichlet point - make a relevant of the solution (Us=Um for slave/master points)
- compute the right hand side of the equation
References EMM_DisplacementOperator::computeMagneticStress(), EMM_RealField::copy(), EMM_DisplacementOperator::getAccelerator(), EMM_DisplacementOperator::getSolver(), EMM_DisplacementOperator::mEquilibriumMatrix, EMM_DisplacementOperator::mUt, MATH_Solver::setMaximumIterationsNumber(), EMM_DisplacementOperator::spaceProjection(), EMM_DisplacementOperator::spaceRelevant(), and tBoolean.
Referenced by EMM_DisplacementOperator::computeEquilibriumMatrixDiagonalConditioner(), and EMM_DisplacementOperator::updateAtNextTimeStep().
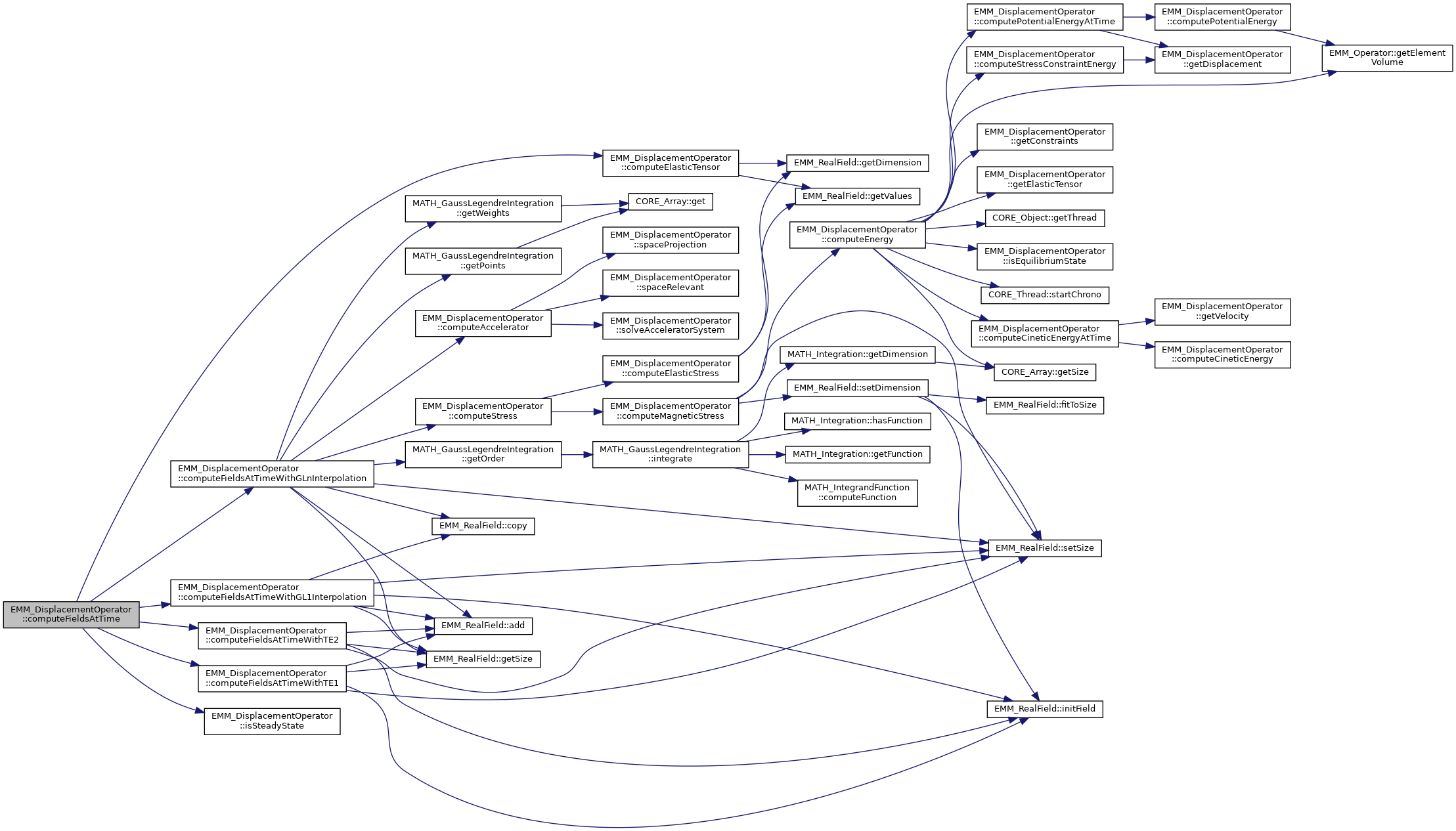
◆ computeFieldsAtTime()
|
virtualinherited |
compute the fields of operator at time
- Parameters
-
t the time order order of integration of the fields sigma the magnetized weight of each cell dM_dt0 the variation of M at time 0 M0 the magnetization field at each point at time t 0
- Returns
- true if the computation has succeeded.
compute fields at time from M and its first time derivative
Implements EMM_Operator.
References EMM_DisplacementOperator::computeElasticTensor(), EMM_DisplacementOperator::computeFieldsAtTimeWithGL1Interpolation(), EMM_DisplacementOperator::computeFieldsAtTimeWithGLnInterpolation(), EMM_DisplacementOperator::computeFieldsAtTimeWithTE1(), EMM_DisplacementOperator::computeFieldsAtTimeWithTE2(), EMM_DisplacementOperator::isSteadyState(), EMM_DisplacementOperator::mAccelerator, EMM_DisplacementOperator::mDt, EMM_DisplacementOperator::mEpsilonUt, EMM_DisplacementOperator::mMs, EMM_DisplacementOperator::mTimeIntegrationMethod, EMM_DisplacementOperator::mTimeIntegrationOrder, EMM_DisplacementOperator::mUn, EMM_DisplacementOperator::mUnm1, EMM_DisplacementOperator::mUs, EMM_DisplacementOperator::mUt, EMM_DisplacementOperator::mVn, EMM_DisplacementOperator::mVt, EMM_DisplacementOperator::P1, tBoolean, EMM_DisplacementOperator::TE, and tFlag.
Referenced by EMM_DisplacementOperator::setCFL().

◆ computeMagneticStress() [1/3]
|
protectedvirtual |
compute the magnetic stress 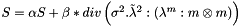 to elastic stress S
to elastic stress S
- Parameters
-
alpha : multiplicator of the total stress beta : mustilicator of the magnetic stress nCells the size of the magnetism value dim dimension of the problem in [1,3] sigma weight of each cell M the magnetization field value nData number of data for the stress D the stress divergence in input the elastic stress , in output the total stress
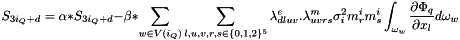 where
where 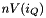 is the cells connected to point at global index
is the cells connected to point at global index 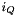 abd q is the local index of
abd q is the local index of 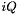 in cell
in cell 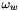 .
.
- pts={[0,0,0],[1,0,0],[0,1,0],[1,1,0],[0,0,1],[1,0,1],[0,1,1],[1,1,1]} local coordinates of cell points.
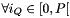 P is the number of points of the domain
P is the number of points of the domain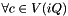
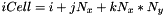 index of the cell c
index of the cell c- if iCell is in magnetized domain
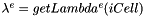 of size 3x3x3x3
of size 3x3x3x3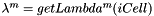 of size 3x3x3x3
of size 3x3x3x3![$ M=M[3*iCell] $](form_708.png) of size 3
of size 3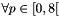 loop on nodes of cell iCell of local coordinate
loop on nodes of cell iCell of local coordinate 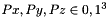 .
.- compute the index of the point iP=(i+Px)+Nx*(j+Py)+Nx.Ny.(k+Pz)
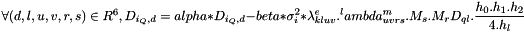
start=iq+Px.(jq+Py.kq)
Implements EMM_DisplacementOperator.
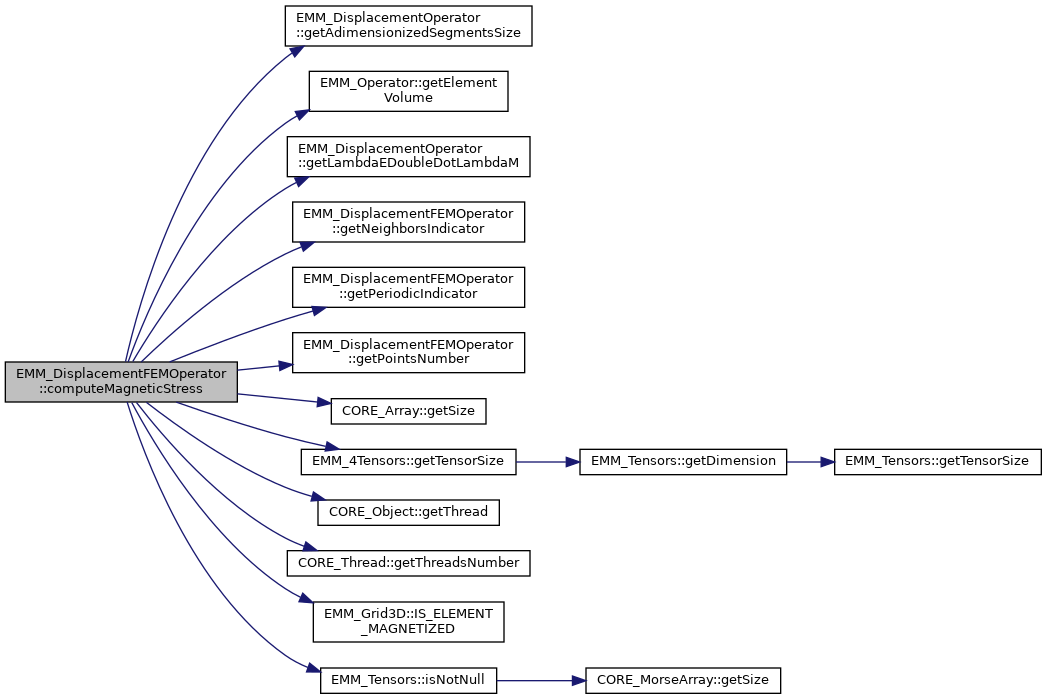
References EMM_Grid3D::ELEMENT_POINTS, EMM_DisplacementOperator::getAdimensionizedSegmentsSize(), EMM_Operator::getElementVolume(), EMM_DisplacementOperator::getLambdaEDoubleDotLambdaM(), getNeighborsIndicator(), getPeriodicIndicator(), getPointsNumber(), CORE_Array< T >::getSize(), EMM_4Tensors::getTensorSize(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), INT_GRAD_PHI, INT_GRAD_PHI_FACTOR, EMM_Grid3D::IS_ELEMENT_MAGNETIZED(), EMM_Tensors::isNotNull(), OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, EMM_Grid3D::POINTS_NUMBER_PER_ELEMENT, tBoolean, tCellFlag, tCInt, tDimension, tInteger, tReal, tUCInt, tUIndex, and tUInteger.
Referenced by EMMG_DisplacementFEMOperator::computeMagneticStress(), and getDataFieldSpace().
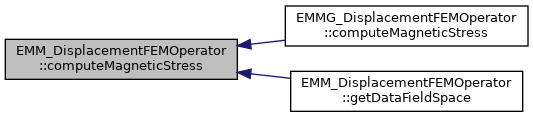
◆ computeMagneticStress() [2/3]
|
inlineinherited |
compute the magnetic stress for all cells 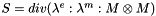
- Parameters
-
[in] sigma magnetized weight for each cell [in] M the magnetization field [out] S the magnetic stress dield
It computes:
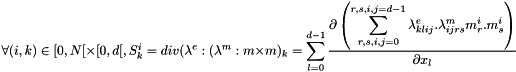 where
where
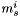 is the s-coordinate of the magnetization field M at cell i when s is in [0,d[ and d is the dimension of the space (i.e. 3).
is the s-coordinate of the magnetization field M at cell i when s is in [0,d[ and d is the dimension of the space (i.e. 3). is the r-coordinate of center of cell
is the r-coordinate of center of cell
References EMM_DisplacementOperator::computeEnergy(), EMM_RealField::setDimension(), EMM_RealField::setSize(), tDimension, tReal, and tUIndex.
Referenced by EMM_DisplacementOperator::computeEquilibriumState(), and EMM_DisplacementOperator::computeStress().
◆ computeMagneticStress() [3/3]
|
pure virtualinherited |
compute the magnetic stress for all cells from the stress 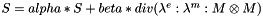
- Parameters
-
[in] alpha : multiplicator factor for S [in] beta : multiplicator factor for magnetic stress [in] sigma the magnetized weight of cells [in] M the magnetization field [in,out] S the total stress field
It computes:
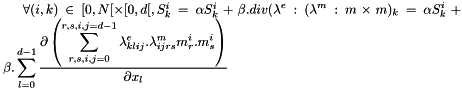 where
where
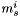 is the s-coordinate of the magnetization field M at cell i when s is in [0,d[ and d is the dimension of the space (i.e. 3).
is the s-coordinate of the magnetization field M at cell i when s is in [0,d[ and d is the dimension of the space (i.e. 3).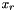 is the r-coordinate of center of cell
is the r-coordinate of center of cell
Implemented in EMMG_DisplacementFVM_VOGGROperator, EMMG_DisplacementFVM_SSGROperator, EMMG_DisplacementFVM_STEGROperator, EMMG_DisplacementFVM_VTEGROperator, and EMMG_DisplacementFEMOperator.
◆ computePotentialEnergy()
|
virtual |
compute the potential energy to the space variation of the displacement
- Parameters
-
U displacement field
- Returns
- potential energy value
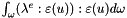
Reimplemented from EMM_DisplacementOperator.
References EMM_DisplacementOperator::computePotentialEnergy().
Referenced by getDataFieldSpace().


◆ computePotentialEnergyAtTime()
|
inlineinherited |
compute the potential energy to the space variation of the displacement
- Parameters
-
t time in [0,dt[ where dt is the time step
- Returns
- potential energy value
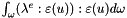
References EMM_DisplacementOperator::computePotentialEnergy(), EMM_DisplacementOperator::getDisplacement(), and tReal.
Referenced by EMM_DisplacementOperator::computeEnergy().

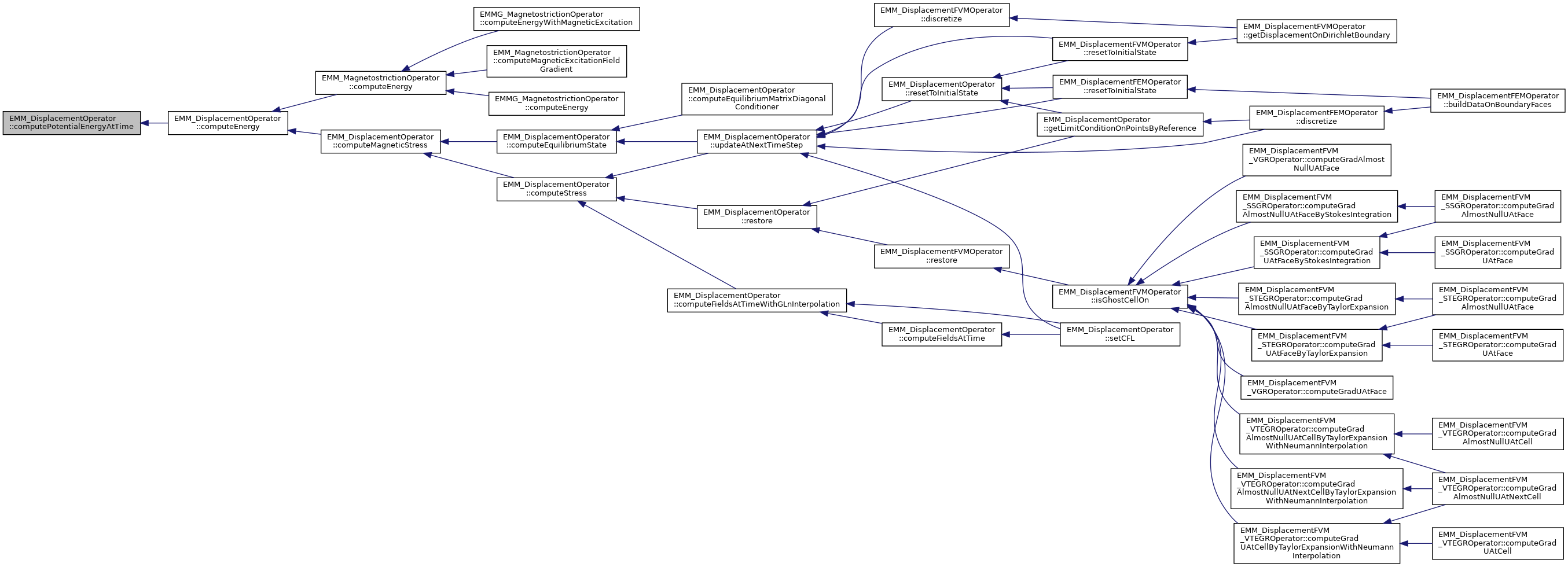
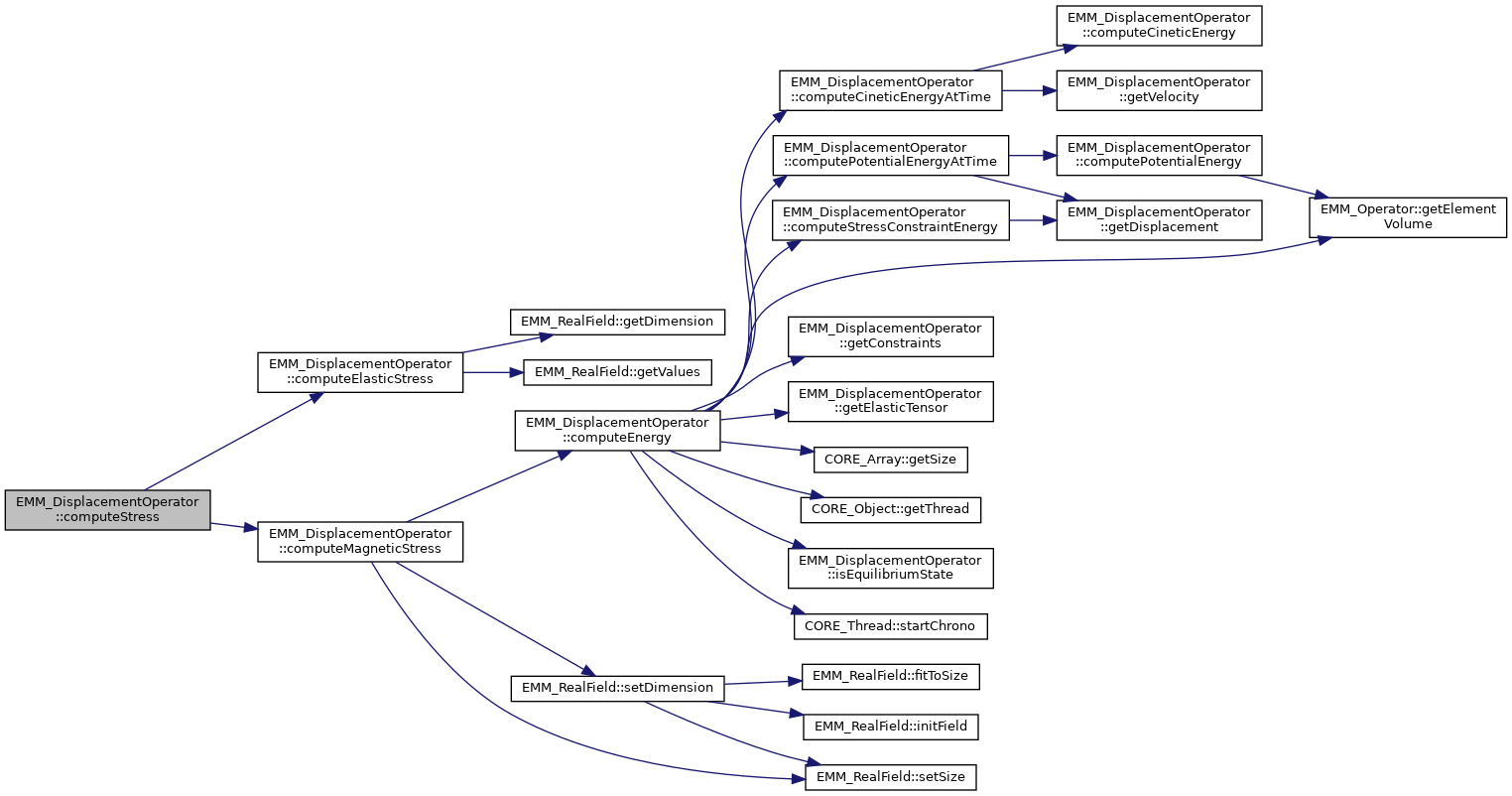
◆ computeStress()
|
inlineinherited |
compute the stress 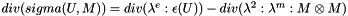
- Parameters
-
sigma magnetized weight for each cell U the displacement field M the magnetization field stress the divergence stress field
It calls:
- EMM_DisplacementOPerator::computeElasticStress();
- EMM_DisplacementOperator::computeMagneticStress();
References EMM_DisplacementOperator::computeElasticStress(), and EMM_DisplacementOperator::computeMagneticStress().
Referenced by EMM_DisplacementOperator::computeFieldsAtTimeWithGLnInterpolation(), EMM_DisplacementOperator::restore(), and EMM_DisplacementOperator::updateAtNextTimeStep().
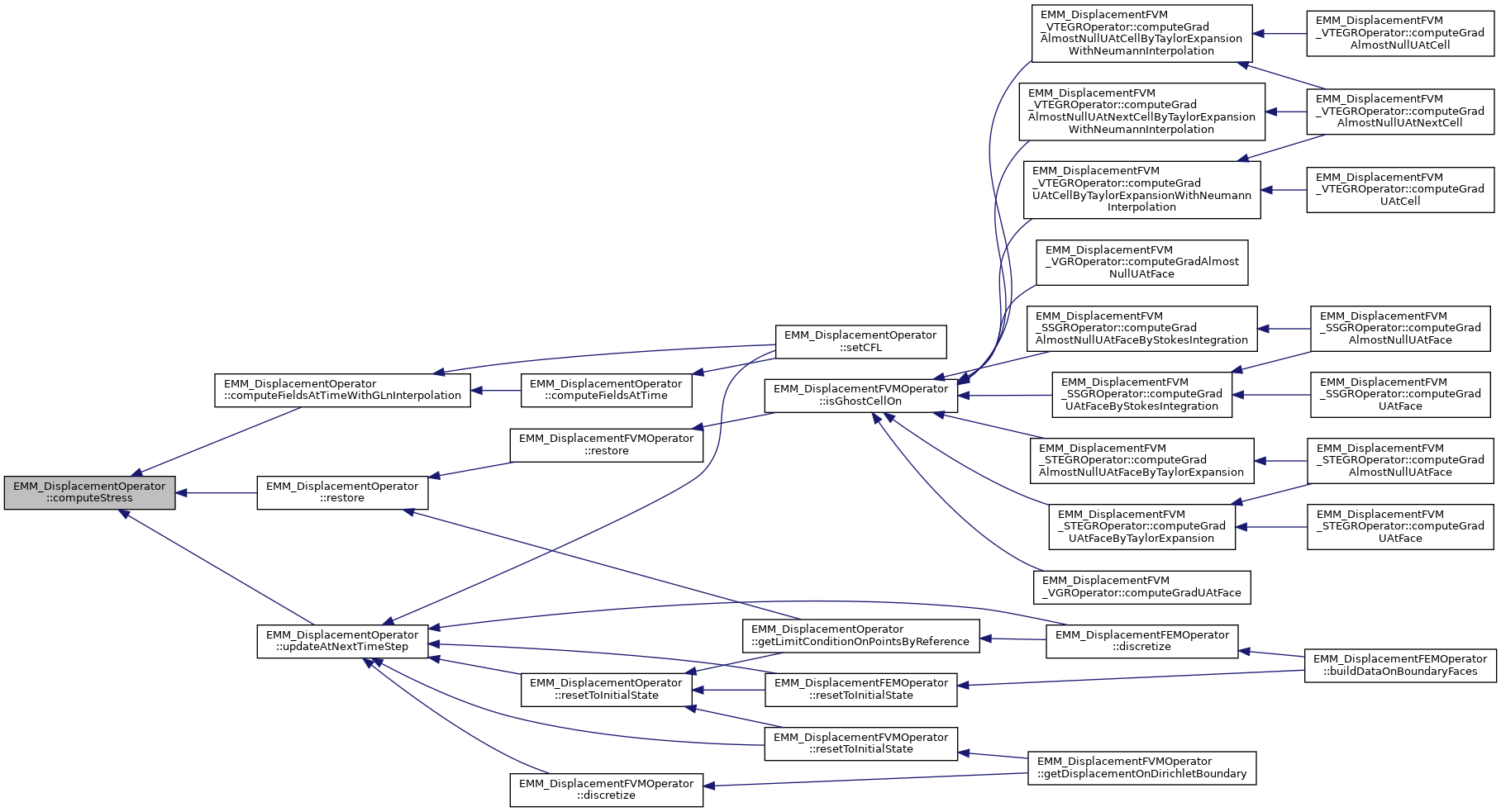
◆ computeStressConstraintEnergy() [1/2]
|
virtual |
compute the stress constraint energy on boundary
- Parameters
-
Uf the displacement field whose Slave point are set from its master point value
- Returns
- the corresponding energy
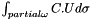
periodicity of the domain
Implements EMM_DisplacementOperator.
References EMM_Grid3D::ELEMENT_POINTS, EMM_Grid3D::FACE_POINTS, EMM_DisplacementOperator::getAdimensionizedSegmentsSize(), EMM_DisplacementOperator::getConstraints(), EMM_RealField::getDimension(), EMM_DisplacementOperator::getLimitConditionOnPoints(), getNeighborsIndicator(), getPeriodicIndicator(), getPointsNumber(), CORE_Array< T >::getSize(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), EMM_RealField::getValues(), iand, EMM_Grid3D::IS_ELEMENT_MAGNETIZED(), EMM_Grid3D::isFaceOnNeumannBoundary(), null, OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT_REDUCTION, EMM_Grid3D::POINTS_NUMBER_PER_FACE, tBoolean, tCellFlag, tDimension, tLimitCondition, tReal, tUCInt, tUIndex, and tUInteger.
Referenced by getDataFieldSpace().
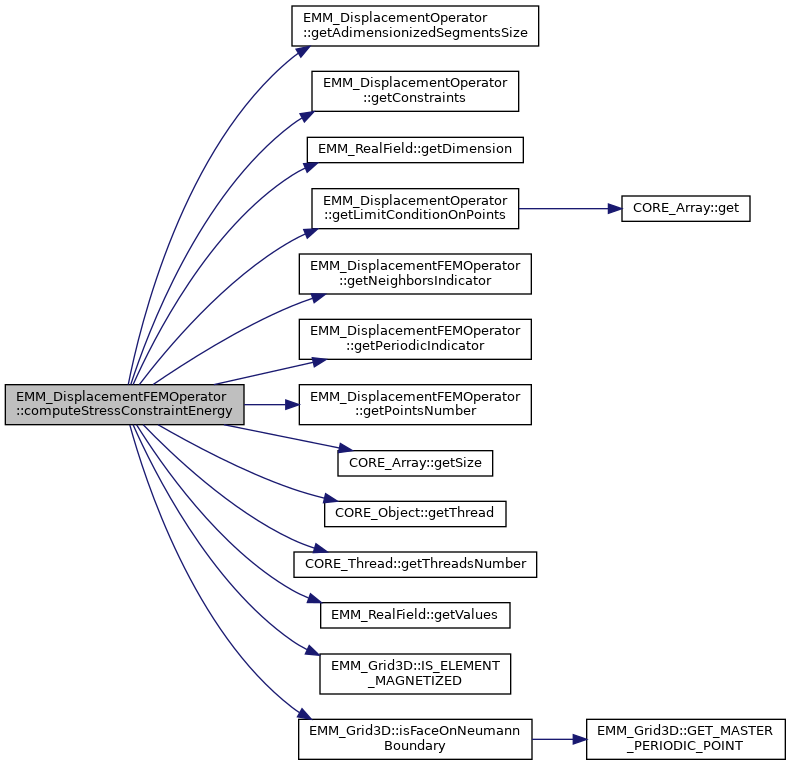

◆ computeStressConstraintEnergy() [2/2]
|
inlineinherited |
compute the energy of the boundary stress constraint
- Parameters
-
t time in [0,dt[ where dt is the time step
References EMM_DisplacementOperator::getDisplacement(), and tReal.
Referenced by EMM_DisplacementOperator::computeEnergy().

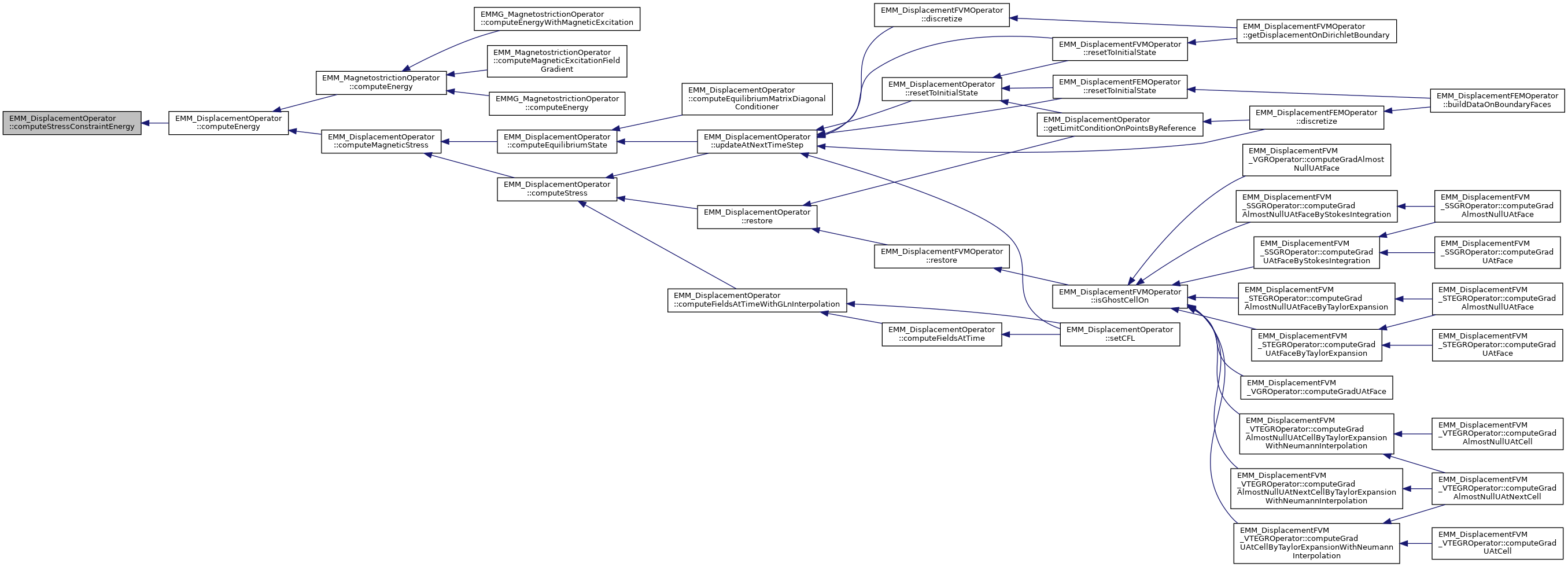
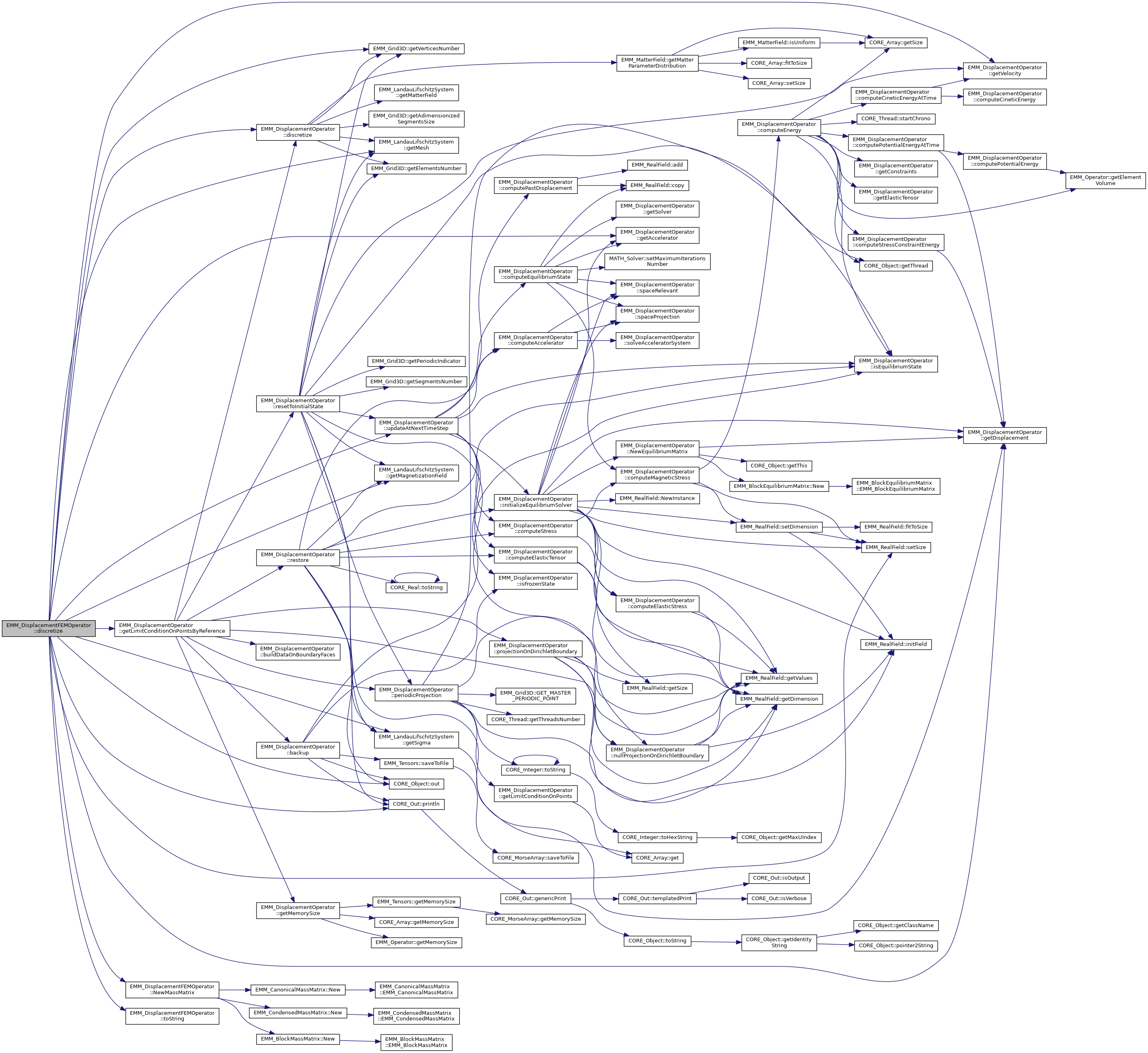
◆ discretize()
|
virtual |
discretize the operator
- Parameters
-
system the data to discretize the operator
- Returns
- true if it succeeds
- call EMM_DisplacementOperator::discretize()
- create the mass matrix
- compute the accelerator vector at t=0
- compute the accelerator and the first time field
Reimplemented from EMM_DisplacementOperator.
References EMM_DisplacementOperator::discretize(), EMM_DisplacementOperator::getAccelerator(), EMM_DisplacementOperator::getDisplacement(), EMM_DisplacementOperator::getLimitConditionOnPointsByReference(), EMM_LandauLifschitzSystem::getMagnetizationField(), EMM_LandauLifschitzSystem::getMesh(), EMM_LandauLifschitzSystem::getSigma(), EMM_DisplacementOperator::getVelocity(), EMM_Grid3D::getVerticesNumber(), mMassMatrix, NewMassMatrix(), CORE_Object::out(), CORE_Out::println(), EMM_RealField::setSize(), tBoolean, toString(), tUIndex, and EMM_DisplacementOperator::updateAtNextTimeStep().
Referenced by buildDataOnBoundaryFaces().

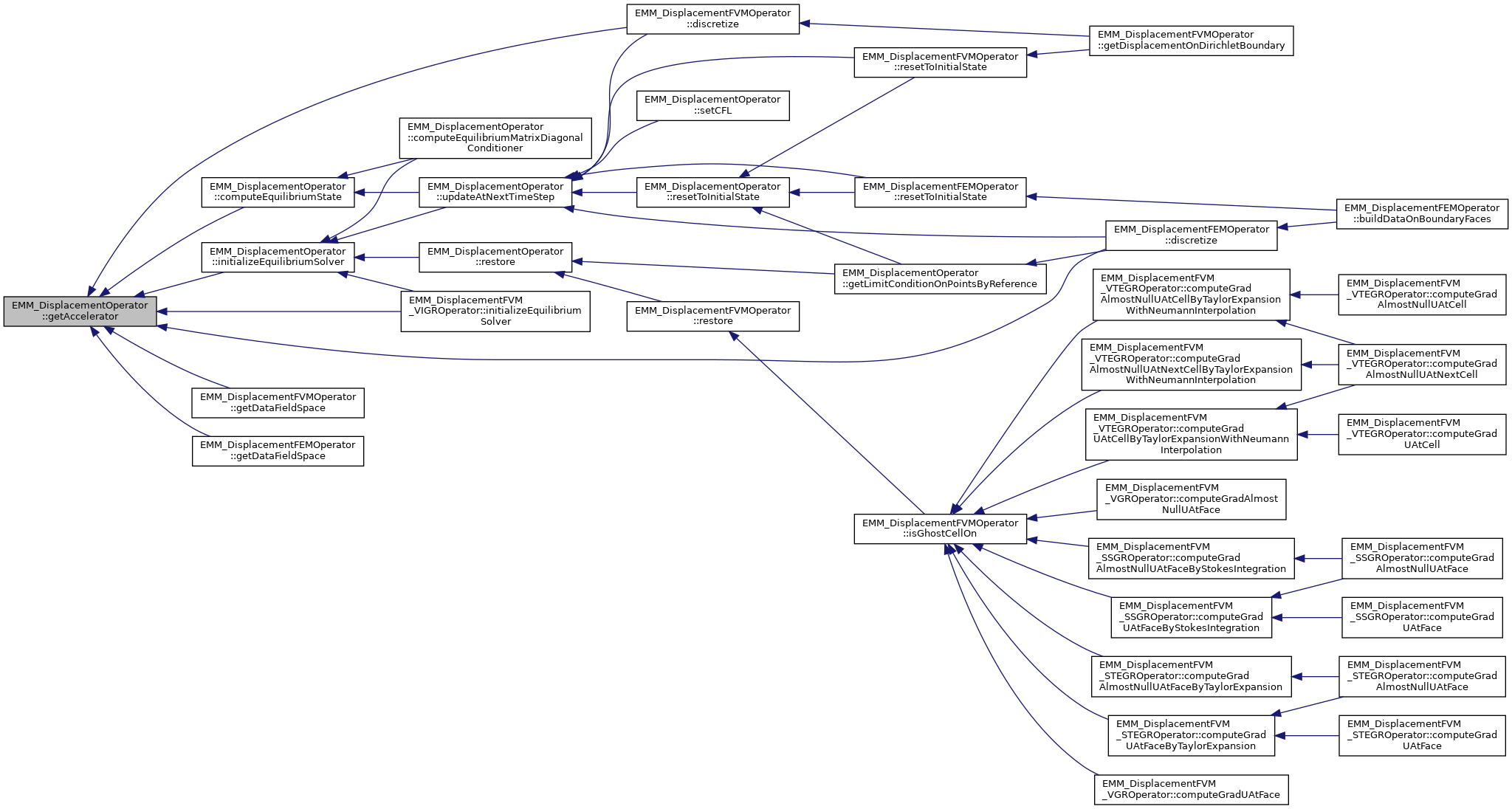
◆ getAccelerator() [1/2]
|
inlineinherited |
get the accelerator for writing
- Returns
- the accelerator field
Referenced by EMM_DisplacementOperator::computeEquilibriumState(), EMM_DisplacementFVMOperator::discretize(), discretize(), EMM_DisplacementFVMOperator::getDataFieldSpace(), getDataFieldSpace(), EMM_DisplacementFVM_VIGROperator::initializeEquilibriumSolver(), and EMM_DisplacementOperator::initializeEquilibriumSolver().
◆ getAccelerator() [2/2]
|
inlineinherited |
get the accelerator for reading
- Returns
- the accelerator field
References EMM_DisplacementOperator::setSolver(), and tString.

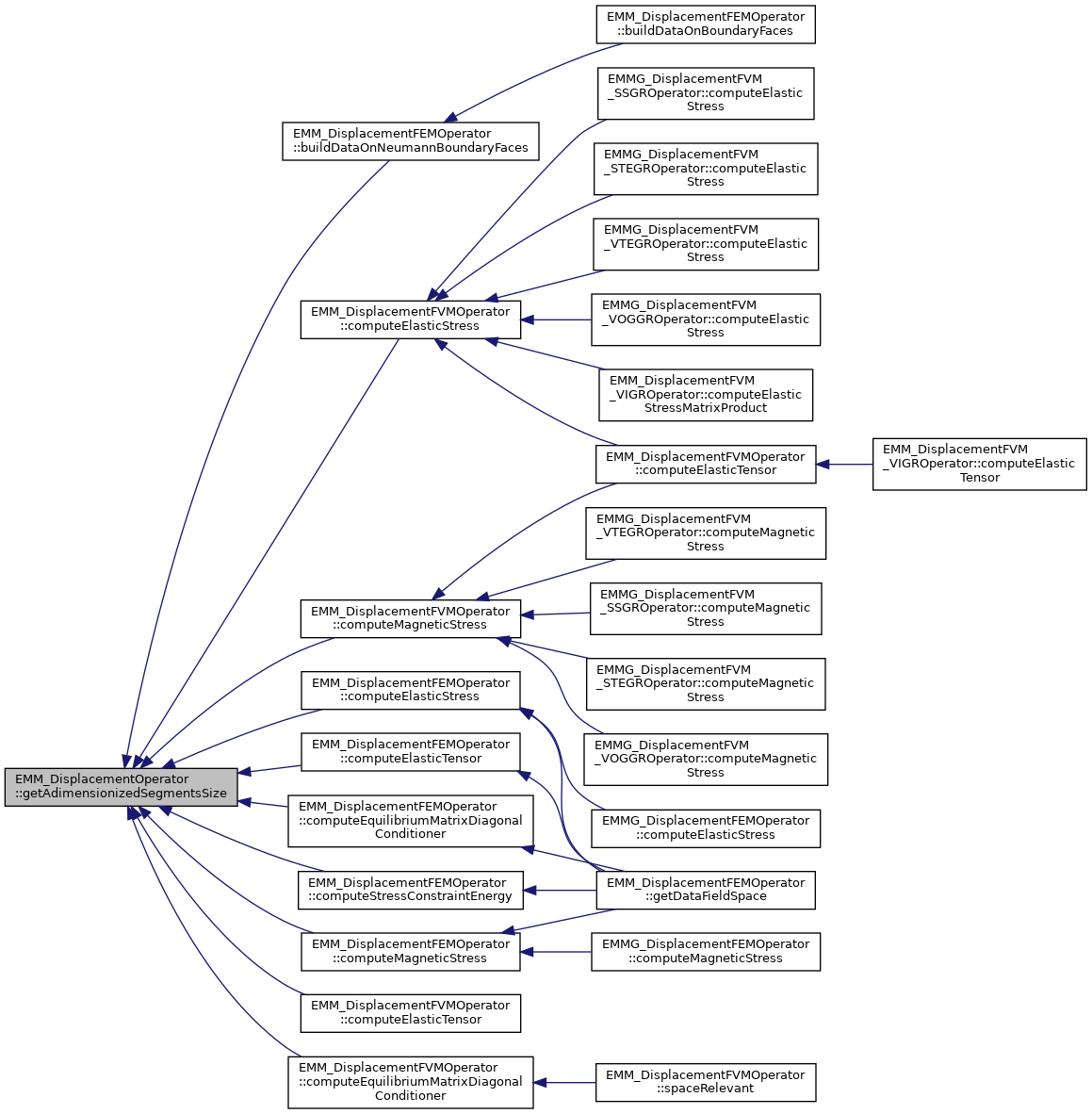
◆ getAdimensionizedSegmentsSize()
|
inlineinherited |
get the segments size in all directions
- Returns
- an array of size 3 which give sthe step size in the i-direction for i in [0,3[
References EMM_DisplacementOperator::mL.
Referenced by buildDataOnNeumannBoundaryFaces(), EMM_DisplacementFVMOperator::computeElasticStress(), computeElasticStress(), EMM_DisplacementFVMOperator::computeElasticTensor(), computeElasticTensor(), EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), computeEquilibriumMatrixDiagonalConditioner(), EMM_DisplacementFVMOperator::computeMagneticStress(), computeMagneticStress(), and computeStressConstraintEnergy().
◆ getAdimensionizedVolumicMass()
|
inlineinherited |
get the adimensionized volumic mass per cell
- Returns
- the adimensionized volumic mass
References EMM_DisplacementOperator::mKappa.
Referenced by EMM_DisplacementFVMOperator::computeCineticEnergy(), and computeCineticEnergy().

◆ getClassName() [1/2]
|
inherited |
return the class name of the object
- Returns
- the class name of the object
References tString.
Referenced by CORE_Object::getIdentityString(), EMM_Operator::getName(), and CORE_Object::isMemoryChecked().

◆ getClassName() [2/2]
return the class name of the object
- Parameters
-
identityString the identity string of the object
- Returns
- the class name
◆ getConstraintFaces()
|
inlineinherited |
get the constraint faces 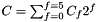
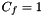 if face f is constrainted
if face f is constrainted
- Returns
- the constraints faces
References EMM_DisplacementOperator::mConstraintFaces.
Referenced by buildDataOnNeumannBoundaryFaces(), and EMM_DisplacementFVMOperator::computeElasticStress().
◆ getConstraints() [1/2]
|
inlineinherited |
get the constraints field for reading
- Returns
- the constraints field
Referenced by addBoundaryElasticStress(), EMM_DisplacementFVMOperator::computeElasticStress(), EMM_DisplacementOperator::computeEnergy(), and computeStressConstraintEnergy().
◆ getConstraints() [2/2]
|
inlineinherited |
get the constraints field for writing
- Returns
- the constraints field
◆ getDataField() [1/3]
|
inlinevirtualinherited |
get the data field at index for saving data in vtk,txt,... files.
- Parameters
-
index index of the field in [0,getDataFieldsNumber()[ dataName name of the field n number of element of the field dim dimension of the field in [1,3[ values values of the field
- Returns
- true if the field at index exists
- 0 : it returns the displacement field U
- 1 : it returns the velocity field dU_dt
- 2 : it returns the accelerator field acc=
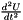
Reimplemented from EMM_Operator.
References tBoolean.
◆ getDataField() [2/3]
|
inlinevirtualinherited |
get the data field at index for saving data in vtk,txt,... files.
- Parameters
-
index index of the field in [0,getDataFieldsNumber()[ dataName name of the field n number of element of the field dim dimension of the field in [1,3[ values values of the field
- Returns
- true if the field at index exists
- 0 : it returns the displacement field U
- 1 : it returns the velocity field dU_dt
- 2 : it returns the accelerator field acc=
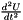
Reimplemented from EMM_Operator.
References tBoolean.
◆ getDataField() [3/3]
|
inlinevirtualinherited |
get the data field at index for saving data in vtk,txt,... files.
- Parameters
-
index index of the field in [0,getDataFieldsNumber()[ dataName name of the field n number of element of the field dim dimension of the field in [1,3[ values values of the field
- Returns
- true if the field at index exists
- 0 : it returns the displacement field U
- 1 : it returns the velocity field dU_dt
- 2 : it returns the accelerator field acc=
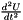
Reimplemented from EMM_Operator.
References tBoolean.
◆ getDataFieldsNumber()
|
inlinevirtualinherited |
get the number of field used in the operator
- Returns
- the number of data
Reimplemented from EMM_Operator.
References EMM_DisplacementOperator::isSteadyState().

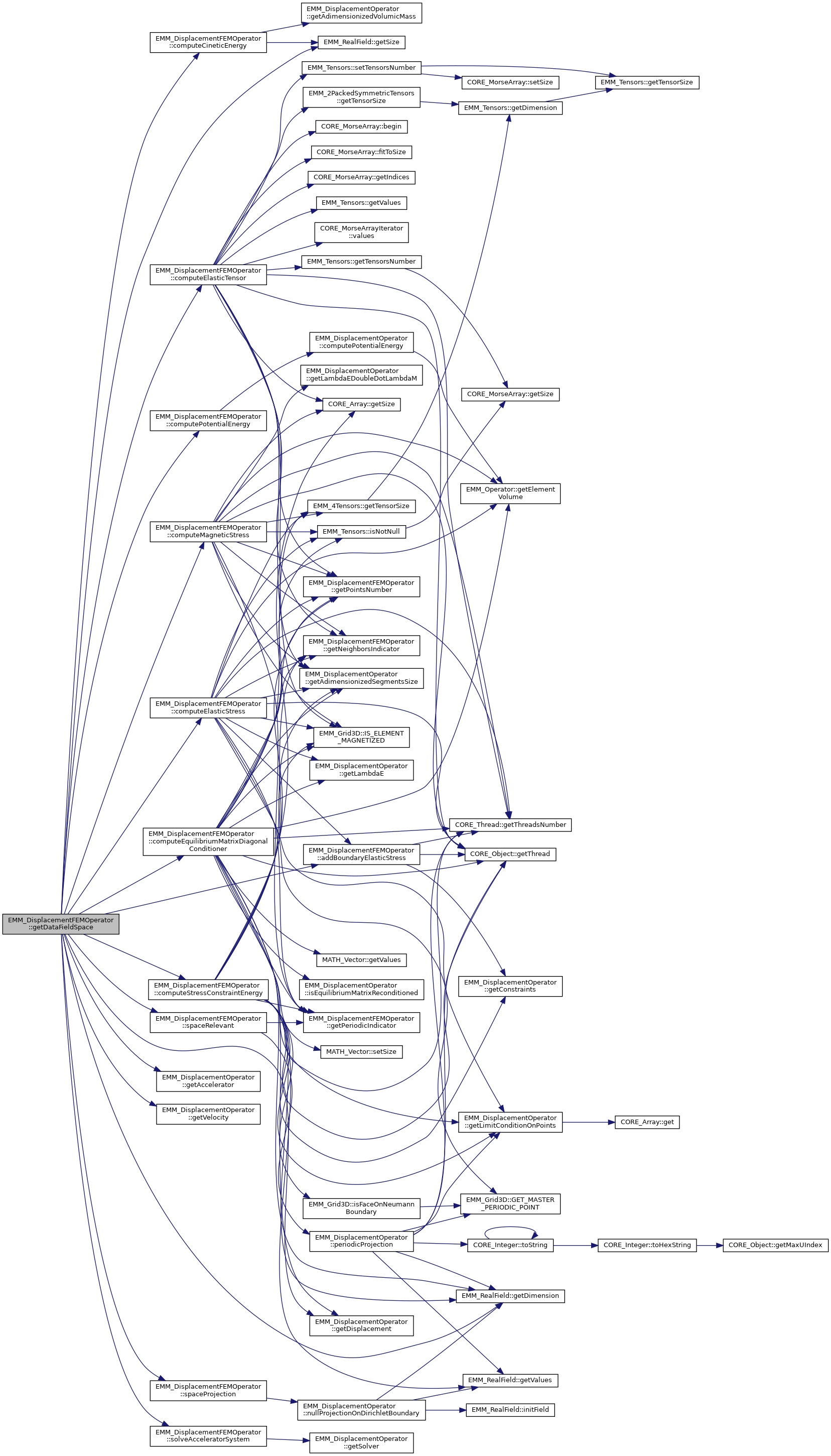
◆ getDataFieldSpace()
|
inlinevirtual |
get the data field at index for saving data in vtk,txt,... files.
- Parameters
-
index index of the field in [0,getDataFieldsNumber()[ dataName name of the field supportType : mesh element whre the field is applied EMM_Grid3D::ELEMENT; || EMM_Grid3D::POINT dFieldType : type of the field double,float,int,.... n number of element of the field dim dimension of the field in [1,3[
- Returns
- true if the field at index exists
Reimplemented from EMM_Operator.
References addBoundaryElasticStress(), computeCineticEnergy(), computeElasticStress(), computeElasticTensor(), computeEquilibriumMatrixDiagonalConditioner(), computeMagneticStress(), computePotentialEnergy(), computeStressConstraintEnergy(), EMM_DisplacementOperator::getAccelerator(), EMM_RealField::getDimension(), EMM_DisplacementOperator::getDisplacement(), EMM_RealField::getSize(), EMM_DisplacementOperator::getVelocity(), EMM_Grid3D::POINT, solveAcceleratorSystem(), spaceProjection(), spaceRelevant(), tBoolean, tDimension, tReal, and tUIndex.
◆ getDisplacement() [1/3]
|
inlineinherited |
get the displacement for writing
- Returns
- the displacement field
Referenced by EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), computeEquilibriumMatrixDiagonalConditioner(), EMM_DisplacementOperator::computePotentialEnergyAtTime(), EMM_DisplacementOperator::computeStressConstraintEnergy(), EMM_DisplacementFVMOperator::discretize(), discretize(), EMM_DisplacementFVMOperator::getDataFieldSpace(), getDataFieldSpace(), EMM_DisplacementFVM_VIGROperator::initializeEquilibriumSolver(), EMM_DisplacementOperator::initializeEquilibriumSolver(), EMM_DisplacementOperator::NewEquilibriumMatrix(), EMM_DisplacementFVMOperator::resetToInitialState(), and EMM_DisplacementOperator::resetToInitialState().
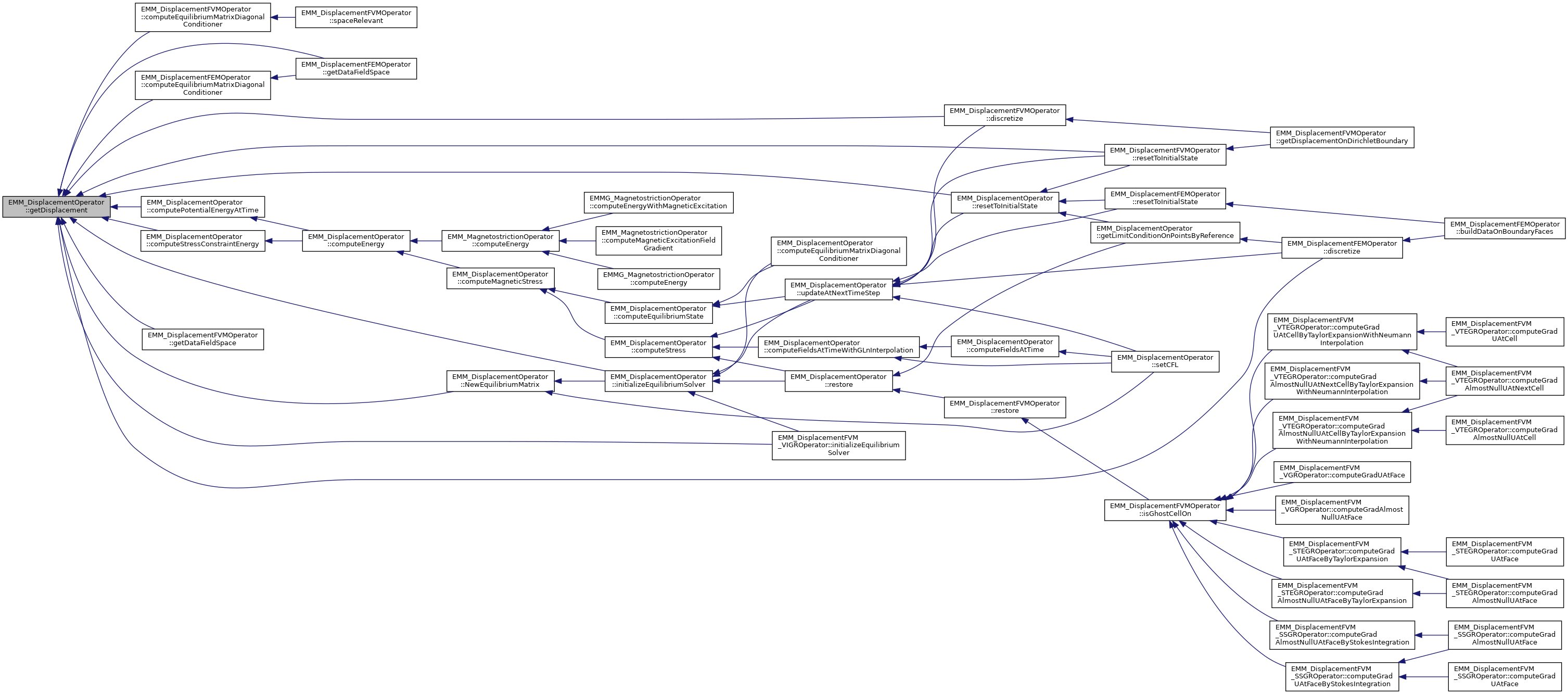
◆ getDisplacement() [2/3]
|
inlineinherited |
get the displacement for reading
- Returns
- the displacement field
◆ getDisplacement() [3/3]
|
inlineinherited |
get the veolicty at time
- Parameters
-
t time to get velocity
References EMM_DisplacementOperator::isSteadyState().

◆ getDoubleEpsilon()
|
inlinestaticinherited |
get the epsilon value for tDouble type
- Returns
- the epsilon value for tDouble type
Referenced by CORE_Test::testType().
◆ getDoubleInfinity()
|
inlinestaticinherited |
get the infinity value for tFloat type
- Returns
- the intinity value for tFloat type
◆ getElasticTensor()
|
inlineinherited |
return the elastic tensor 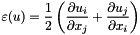
- Returns
- the aelastic tensor
References EMM_DisplacementOperator::mEpsilonUt.
Referenced by EMM_DisplacementOperator::computeEnergy().
◆ getElementVolume()
|
inlineinherited |
return the adimensionized volume of the element
- Returns
- the voume of the element with adimensionized dimensions
References EMM_Operator::mElementVolume.
Referenced by EMM_DisplacementFVMOperator::computeCineticEnergy(), computeElasticStress(), EMM_StaticMagneticTensorOperator::computeEnergy(), EMM_ZeemanOperator::computeEnergy(), EMM_CubicAnisotropyOperator::computeEnergy(), EMM_MagnetostrictionOperator::computeEnergy(), EMM_DisplacementOperator::computeEnergy(), EMM_MagneticExcitationLinearOperator::computeEnergyWithMagneticExcitation(), EMM_AnisotropyOperator::computeEnergyWithMagneticExcitation(), EMM_ZeemanOperator::computeEnergyWithMagneticExcitation(), computeEquilibriumMatrixDiagonalConditioner(), computeMagneticStress(), and EMM_DisplacementOperator::computePotentialEnergy().
◆ getEpsilon()
|
inlinestaticinherited |
get the epsilon value for T type
- Returns
- the epsilon value for T type
◆ getFloatEpsilon()
|
inlinestaticinherited |
get the epsilon value for tFloat type
- Returns
- the epsilon value for tFloat type
Referenced by CORE_Test::testType().
◆ getFloatInfinity()
|
inlinestaticinherited |
get the infinity value for tFloat type
- Returns
- the intinity value for tFloat type
◆ getIdentityString()
|
inlineinherited |
return the identity string of the object of the form className_at_address
- Returns
- the identity string of the object
References CORE_Object::getClassName(), CORE_Object::pointer2String(), and tString.
Referenced by MATH_GaussLegendreIntegration::copy(), EMM_MultiScaleGrid::initialize(), CORE_Object::isInstanceOf(), CORE_Object::printObjectsInMemory(), MATH_Matrix::toString(), EMMG_SLPeriodicMultiScale::toString(), EMM_Stepper::toString(), EMM_AnisotropyDirectionsField::toString(), EMM_BlockMassMatrix::toString(), CORE_Object::toString(), EMM_Tensors::toString(), EMM_MultiScaleGrid::toString(), EMM_MatterField::toString(), EMM_Grid3D::toString(), and EMM_LandauLifschitzSystem::toString().

◆ getInfinity()
|
inlinestaticinherited |
get the infinity for T type
- Returns
- the infinity value for T type
◆ getLambdaE()
|
inlineinherited |
return the adimensionized elastic tensor distribution 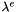
- Returns
- the adimensionized elastic tensor of size 3x3x3x3 at each cell of size nCells in a morse array
Referenced by EMM_DisplacementFVMOperator::computeElasticStress(), computeElasticStress(), EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), and computeEquilibriumMatrixDiagonalConditioner().
◆ getLambdaEDoubleDotLambdaM()
|
inlineinherited |
return the adimensionized magnetic tensor distribution 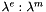
- Returns
- the adimensionized magnetic tensor of size 3x3x3x3 at each cell of size nCells in a morse array
Referenced by EMM_DisplacementFVMOperator::computeMagneticStress(), and computeMagneticStress().
◆ getLambdaMDoubleDotLambdaE()
|
inlineinherited |
return the adimensionized magnetic tensor distribution 
- Returns
- the adimensionized magnetic tensor of size 3x3x3x3 at each cell of size nCells in a morse array
◆ getLambdaMDoubleDotLambdaEDoubleDotLambdaM()
|
inlineinherited |
return the adimensionized magnetic tensor distribution 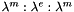
- Returns
- the adimensionized magnetic tensor of size 3x3x3x3 at each cell of size nCells in a morse array
Referenced by EMM_MagnetostrictionOperator::computeEnergy().

◆ getLDoubleEpsilon()
|
inlinestaticinherited |
get the epsilon value for tLDouble type
- Returns
- the epsilon value for tLDouble type
Referenced by CORE_Test::testType().

◆ getLDoubleInfinity()
|
inlinestaticinherited |
get the infinity value for tDouble type
- Returns
- the infinity value for tDouble type
◆ getLimitConditionOnPoints()
|
inlineinherited |
References CORE_Array< T >::get().
Referenced by EMM_DisplacementFVMOperator::computeElasticStress(), computeElasticStress(), EMM_DisplacementFVM_VIGROperator::computeElasticStressMatrixProduct(), EMM_DisplacementFVM_VIGROperator::computeElasticTensor(), EMM_DisplacementFVMOperator::computeElasticTensor(), EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), computeEquilibriumMatrixDiagonalConditioner(), EMM_DisplacementFVM_VOGGROperator::computeGradAlmostNullUAtCellByOstrogradskiGreenIntegration(), EMM_DisplacementFVM_VTEGROperator::computeGradAlmostNullUAtCellByTaylorExpansionWithNeumannInterpolation(), EMM_DisplacementFVM_VOGGROperator::computeGradAlmostNullUAtNextCellByOstrogradskiGreenIntegration(), computeStressConstraintEnergy(), EMM_DisplacementFVM_VIGROperator::initializeEquilibriumSolver(), EMM_DisplacementOperator::nullProjectionOnDirichletBoundary(), EMM_DisplacementOperator::periodicProjection(), and EMM_DisplacementOperator::projectionOnDirichletBoundary().

◆ getLimitConditionOnPointsByReference()
|
inlineinherited |
References EMM_DisplacementOperator::backup(), EMM_DisplacementOperator::buildDataOnBoundaryFaces(), EMM_DisplacementOperator::discretize(), EMM_DisplacementOperator::getMemorySize(), EMM_DisplacementOperator::mLimitConditionOnPoints, EMM_DisplacementOperator::nullProjectionOnDirichletBoundary(), EMM_DisplacementOperator::periodicProjection(), EMM_DisplacementOperator::projectionOnDirichletBoundary(), EMM_DisplacementOperator::resetToInitialState(), EMM_DisplacementOperator::restore(), tBoolean, tCellFlag, tDimension, tReal, tString, tUIndex, tUInteger, and tULLInt.
Referenced by discretize().

◆ getMassMatrixType()
|
inline |
get the mass matrix type
- Returns
- the mass matrix type CANONICAL,BLOCK,CONDENSED
References mMassMatrixType, and NewMassMatrix().

◆ getMaxChar()
|
inlinestaticinherited |
get the max value for tChar type
- Returns
- the max value for tChar type
Referenced by CORE_Test::testType().

◆ getMaxDouble()
|
inlinestaticinherited |
get the max value for tDouble type
- Returns
- the max value for tDouble type
Referenced by CORE_Test::testType().
◆ getMaxFlag()
|
inlinestaticinherited |
get the max value for the tFlag type
- Returns
- the max value for the tFlag type
Referenced by CORE_Test::testType().

◆ getMaxFloat()
|
inlinestaticinherited |
get the max value for tFloat type
- Returns
- the max value for tFloat type
Referenced by CORE_Test::testType().
◆ getMaxIndex()
|
inlinestaticinherited |
get the max value for the array/vector indexing type
- Returns
- the max value for the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMaxInt()
|
inlinestaticinherited |
get the max value for tInt type
- Returns
- the max value for tInt type
Referenced by MATSGN_FFT::fastFourierTransform3D_FFTW(), and CORE_Test::testType().

◆ getMaxInteger()
|
inlinestaticinherited |
get the max value for the integer type
- Returns
- the max value for the integer type
Referenced by CORE_Test::testType().
◆ getMaxLDouble()
|
inlinestaticinherited |
get the max value for tLDouble type
- Returns
- the max value for tLDouble type
Referenced by CORE_Test::testType().
◆ getMaxLInt()
|
inlinestaticinherited |
get the max value for tLInt type
- Returns
- the max value for tLInt type
Referenced by CORE_Test::testType().

◆ getMaxLLInt()
|
inlinestaticinherited |
get the max value for tULInt type
- Returns
- the max value for tULInt type
Referenced by CORE_Test::testType().
◆ getMaxReal()
|
inlinestaticinherited |
get the max value for the real type
- Returns
- he max value for the real type
Referenced by EMM_MatterField::adimensionize(), and CORE_Test::testType().

◆ getMaxSInt()
|
inlinestaticinherited |
get the max value for tSInt type
- Returns
- the max value for tSInt type
Referenced by CORE_Test::testType().
◆ getMaxUChar()
|
inlinestaticinherited |
get the max value for tUChar type
- Returns
- the max value for tUChar type
Referenced by CORE_Test::testType().
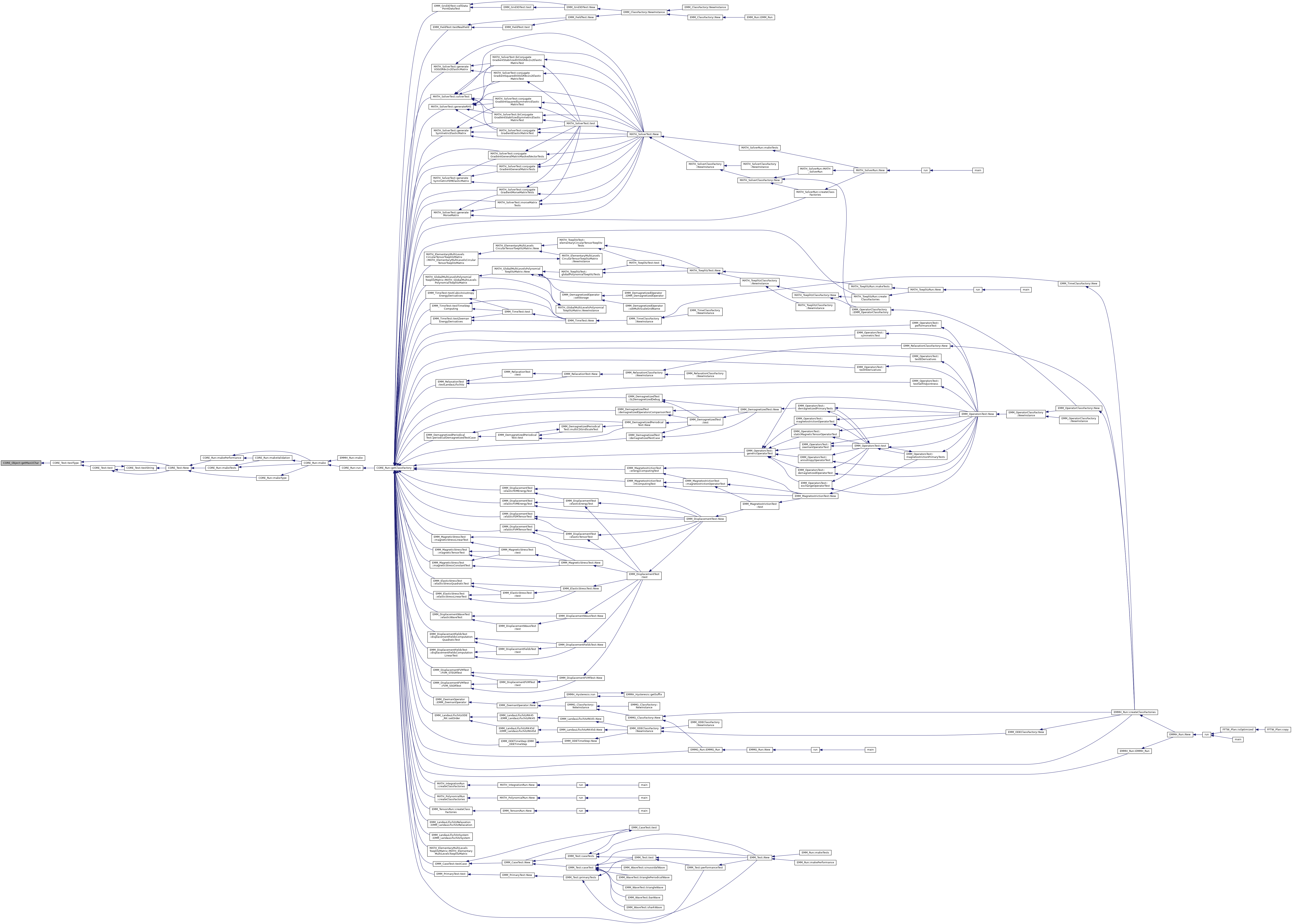
◆ getMaxUIndex()
|
inlinestaticinherited |
get the max value for difference the array/vector indexing type
- Returns
- the max value for difference the array/vector indexing type
Referenced by CORE_Vector< T >::addAfterIndices(), CORE_Vector< T >::search(), CORE_Test::testType(), CORE_Integer::toHexString(), and CORE_Integer::toString().
◆ getMaxUInt()
|
inlinestaticinherited |
get the max value for tUInt type
- Returns
- the max value for tUInt type
Referenced by EMM_Array< tCellFlag >::loadFromFile(), EMM_RealField::loadFromFile(), and CORE_Test::testType().

◆ getMaxUInteger()
|
inlinestaticinherited |
get the max value for the unsigned integer type
- Returns
- the max value for the unsigned integer type
Referenced by MATH_Pn::computeExtrenums(), EMM_MultiScaleGrid::computeLevelsNumber(), EMM_Input::restoreBackup(), MATH_P0::solve(), and CORE_Test::testType().

◆ getMaxULInt()
|
inlinestaticinherited |
get the max value for tULInt type
- Returns
- the max value for tULInt type
Referenced by CORE_Test::testType().
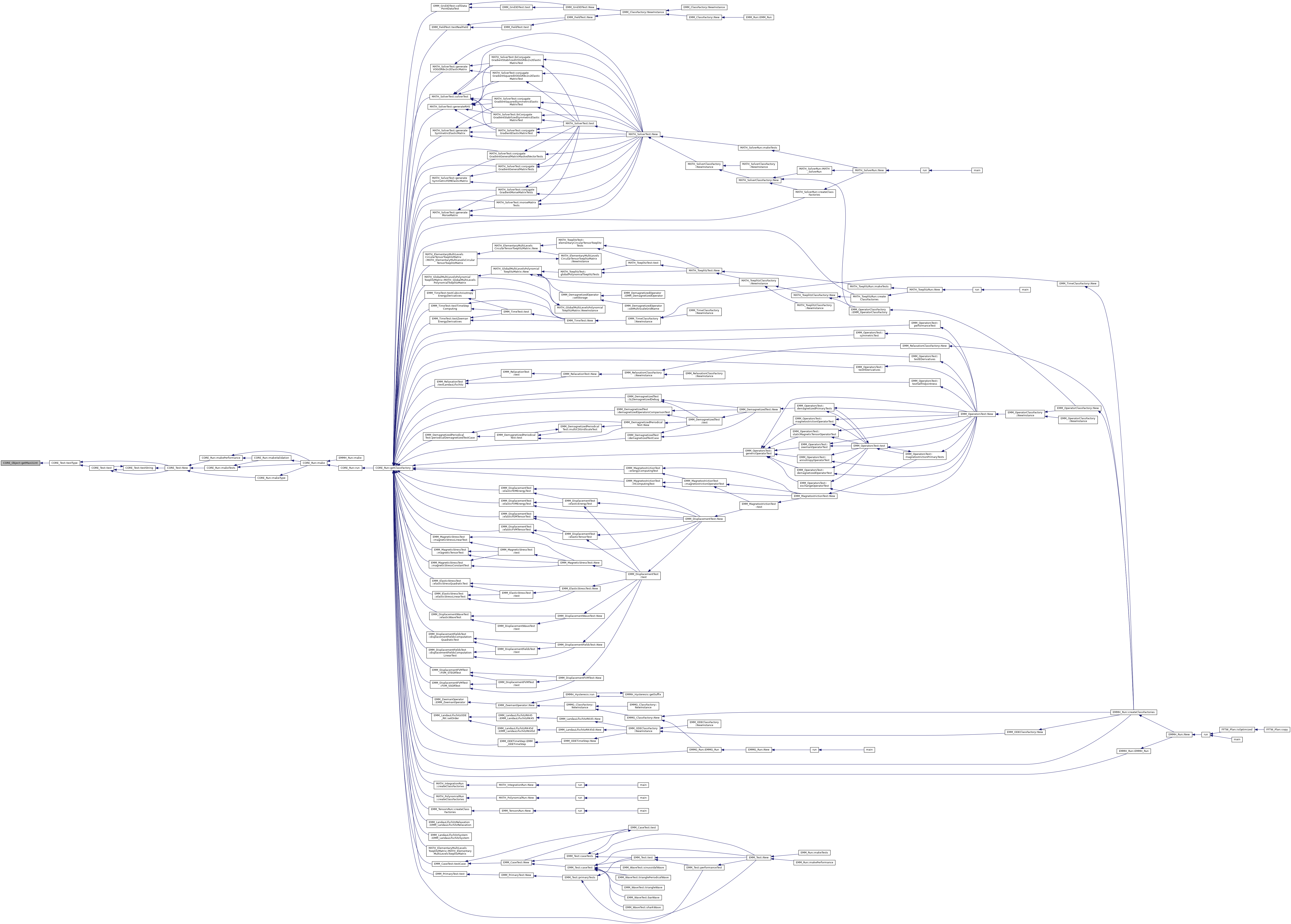
◆ getMaxULLInt()
|
inlinestaticinherited |
get the max value for tULLInt type
- Returns
- the max value for tULLInt type
Referenced by CORE_Test::testType().
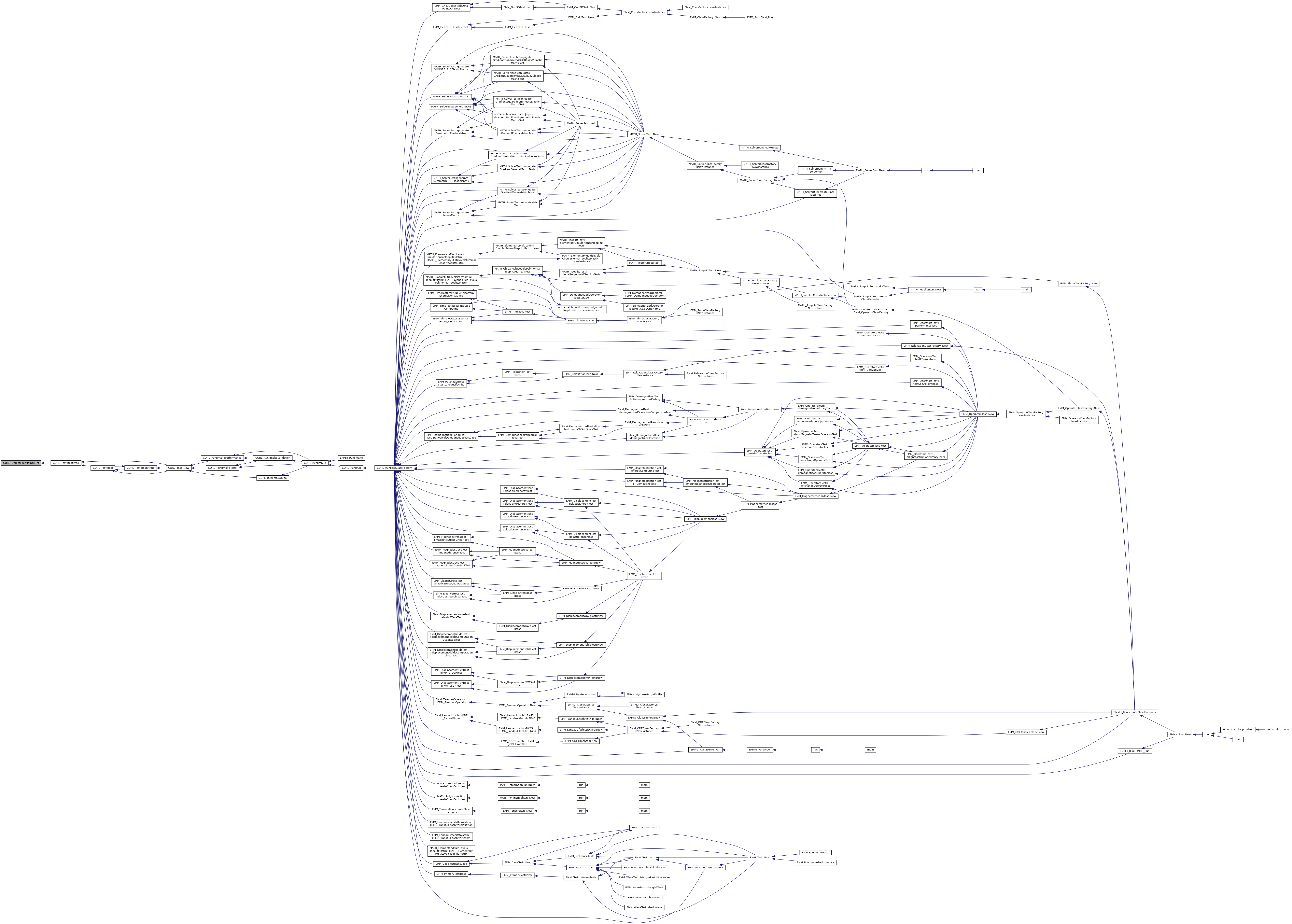
◆ getMaxUSInt()
|
inlinestaticinherited |
get the max value for tUSInt type
- Returns
- the max value for tUSInt type
Referenced by CORE_Test::testType().

◆ getMemorySize()
|
inlinevirtual |
return the memory size in byte
- Returns
- the memory size of the storage in bytes 1 Kb = 1024 bytes 1 Mb = 1024 Kb 1 Gb = 1024 Mb 1 Tb = 1024 Gb 1 Hb = 1024 Tb
Reimplemented from EMM_DisplacementOperator.
References EMM_DisplacementOperator::getMemorySize().

◆ getMinChar()
|
inlinestaticinherited |
get the min value for tChar type
- Returns
- the min value for tChar type
Referenced by CORE_Test::testType().
◆ getMinDouble()
|
inlinestaticinherited |
get the min value for tDouble type
- Returns
- the min value for tDouble type
Referenced by CORE_Test::testType().

◆ getMinFlag()
|
inlinestaticinherited |
get the min value for the tFlag type
- Returns
- the min value for the tFlag type
Referenced by CORE_Test::testType().
◆ getMinFloat()
|
inlinestaticinherited |
get the min value for tFloat type
- Returns
- the min value for tFloat type
Referenced by CORE_Test::testType().
◆ getMinIndex()
|
inlinestaticinherited |
get the min value for the array/vector indexing type
- Returns
- the min value for the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMinInt()
|
inlinestaticinherited |
get the min value for tInt type
- Returns
- the min value for tInt type
Referenced by CORE_Test::testType().
◆ getMinInteger()
|
inlinestaticinherited |
get the min value for the integer type
- Returns
- the minin value for the integer type
Referenced by CORE_Test::testType().

◆ getMinLDouble()
|
inlinestaticinherited |
get the min value for tLDouble type
- Returns
- the min value for tLDouble type
Referenced by CORE_Test::testType().

◆ getMinLInt()
|
inlinestaticinherited |
get the min value for tLInt type
- Returns
- the min value for tLInt type
Referenced by CORE_Test::testType().
◆ getMinLLInt()
|
inlinestaticinherited |
get the min value for tLLInt type
- Returns
- the min value for tLLInt type
Referenced by CORE_Test::testType().

◆ getMinReal()
|
inlinestaticinherited |
get the min value for the real type
- Returns
- the min value for the real type
Referenced by CORE_Test::testType().
◆ getMinSInt()
|
inlinestaticinherited |
get the min value for tSInt type
- Returns
- the min value for tSInt type
Referenced by CORE_Test::testType().
◆ getMinUChar()
|
inlinestaticinherited |
get the min value for tUChar type
- Returns
- the min value for tUChar type
Referenced by CORE_Test::testType().
◆ getMinUIndex()
|
inlinestaticinherited |
get the min value for difference the array/vector indexing type
- Returns
- the min value for difference the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMinUInt()
|
inlinestaticinherited |
get the min value for tUInt type
- Returns
- the min value for tUInt type
Referenced by CORE_Test::testType().
◆ getMinUInteger()
|
inlinestaticinherited |
get the min value for the unsigned integer type
- Returns
- the min value for the unsigned integer type
Referenced by CORE_Test::testType().

◆ getMinULInt()
|
inlinestaticinherited |
get the min value for tULInt type
- Returns
- the min value for tULInt type
Referenced by CORE_Test::testType().

◆ getMinULLInt()
|
inlinestaticinherited |
get the min value for tULLInt type
- Returns
- the min value for tULLInt type
Referenced by CORE_Test::testType().
◆ getMinUSInt()
|
inlinestaticinherited |
get the min value for tUSInt type
- Returns
- the min value for tUSInt type
Referenced by CORE_Test::testType().
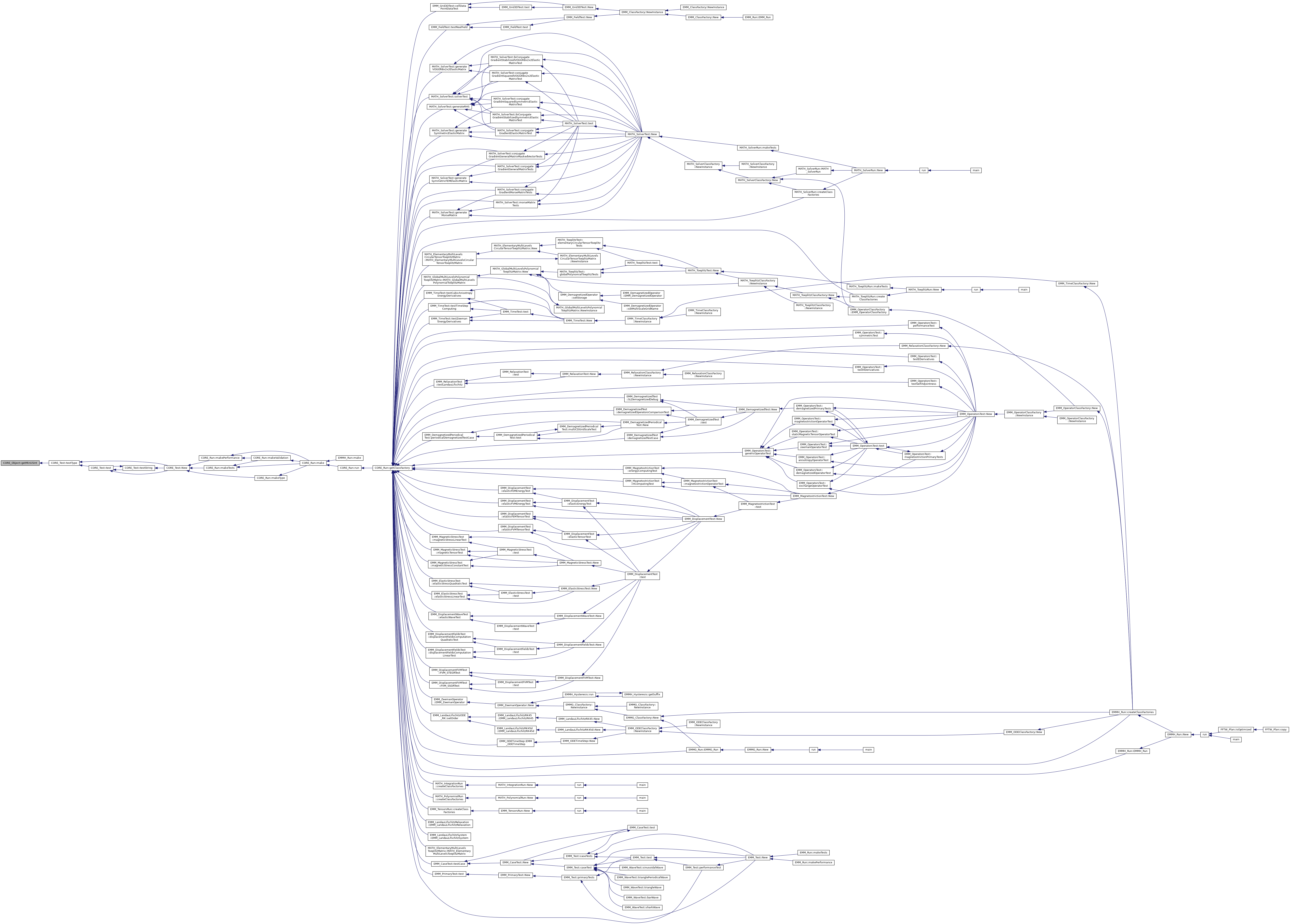
◆ getName()
|
inlinevirtualinherited |
return an human reading name of the operator
- Returns
- the name of the operator
References CORE_Object::getClassName(), EMM_Operator::isAffine(), EMM_Operator::isGradientComputationable(), tBoolean, tString, and tUIndex.
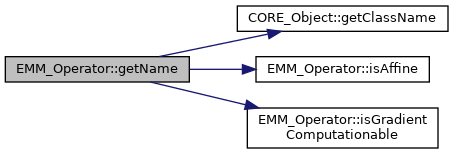
◆ getNeighborsIndicator()
|
inline |
return the neighbors indicator in bits 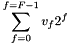 where F is the number of faces per element and
where F is the number of faces per element and 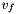 is 1 if there is a neighbor cell with the face f
is 1 if there is a neighbor cell with the face f
Referenced by computeElasticStress(), computeElasticTensor(), computeEquilibriumMatrixDiagonalConditioner(), computeMagneticStress(), and computeStressConstraintEnergy().
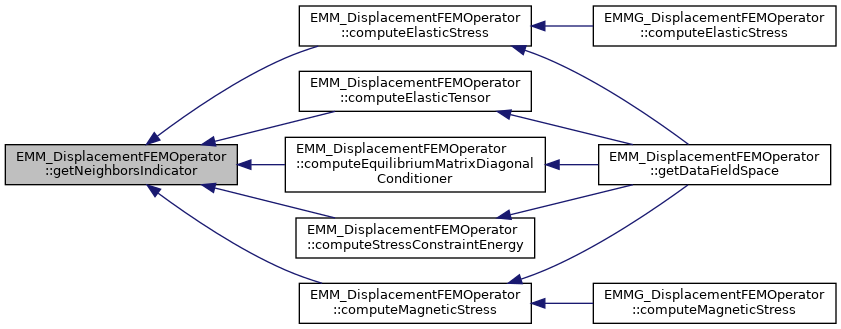
◆ getOut()
|
inlinestaticinherited |
◆ getPeriodicIndicator()
|
inline |
get the periodicity indication
- Returns
- the periodicity indicator in bits:
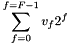 where F is the number of faces per element and
where F is the number of faces per element and 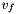 is 1 if there is a periodiity in the face f
is 1 if there is a periodiity in the face f
Referenced by computeElasticStress(), computeEquilibriumMatrixDiagonalConditioner(), computeMagneticStress(), computeStressConstraintEnergy(), and spaceRelevant().
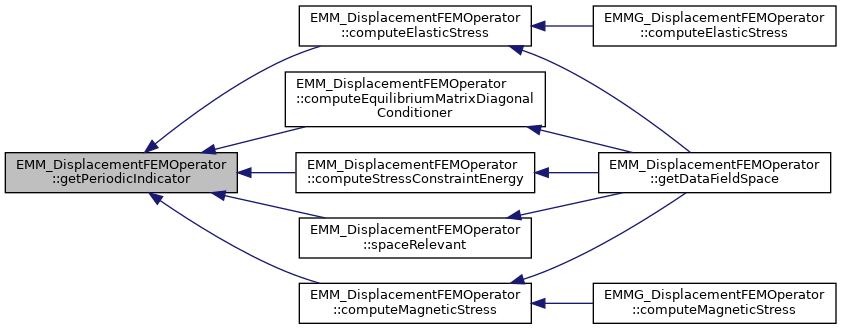
◆ getPointerAddress()
|
inlineinherited |
return the identity string of the object
- Returns
- the identity string of the object
References CORE_Object::pointer2String().

◆ getPointsNumber()
|
inline |
get the points number in each direction
- Returns
- the array containing the points number of size 3
Referenced by computeElasticStress(), computeElasticTensor(), computeEquilibriumMatrixDiagonalConditioner(), computeMagneticStress(), and computeStressConstraintEnergy().
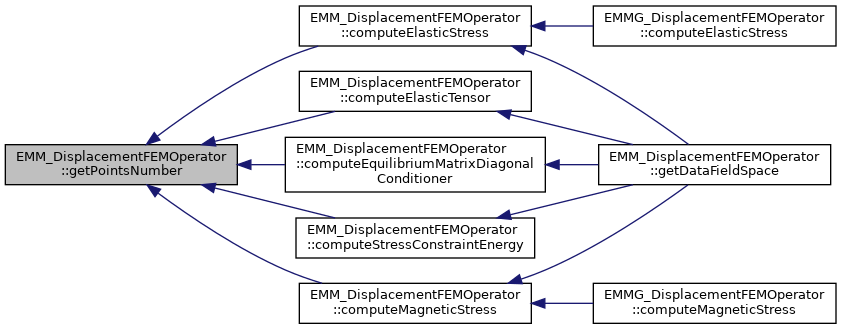
◆ getRealEpsilon()
|
inlinestaticinherited |
get the eps which is the difference between 1 and the least value greater than 1 that is representable.
- Returns
- the eps which is the difference between 1 and the least value greater than 1 that is representable.
Referenced by MATH_P4::solveP4De(), and CORE_Test::testType().
◆ getRealInfinity()
|
inlinestaticinherited |
get the infinity value
- Returns
- the inifinity value for the real type
Referenced by BrentFunction::BrentFunction(), EMM_OperatorsTest::compareDiscretizedData(), EMM_IterativeTimeStep::EMM_IterativeTimeStep(), EMM_SLElementaryDemagnetizedMatrix::Kxy(), NRFunction::NRFunction(), EMM_PolynomialInterpolationTimeStep::optimizeTimeFunction(), and CORE_Test::testType().
◆ getSharedPointer() [1/2]
|
inlineinherited |
get the shared pointer of this class into p
- Parameters
-
p : shared pointer of the class This
Referenced by CORE_Map< Key, Value >::getSharedPointer(), CORE_ArrayList< tString >::getSharedPointer(), EMM_Array< tCellFlag >::getSharedPointer(), CORE_Array< tCellFlag >::getSharedPointer(), CORE_MorseArray< tUChar >::getSharedPointer(), CORE_Vector< T >::getSharedPointer(), and CORE_Object::printObjectsInMemory().
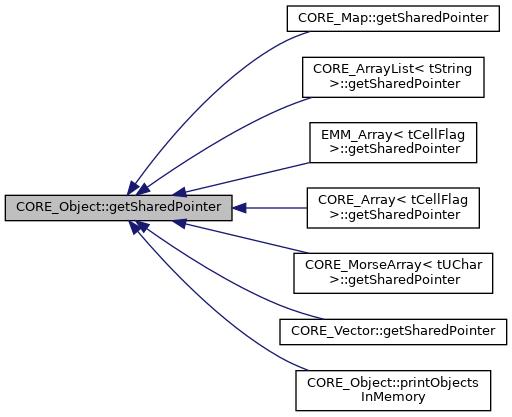
◆ getSharedPointer() [2/2]
|
inlineinherited |
get the shared pointer of this class into p
- Parameters
-
p : shared pointer of the class This
◆ getSolver()
|
inlineinherited |
get the solver of the system
- Returns
- the solver null by default
Referenced by EMM_DisplacementOperator::computeEquilibriumState(), EMMG_ClassFactory::NewInstance(), and solveAcceleratorSystem().
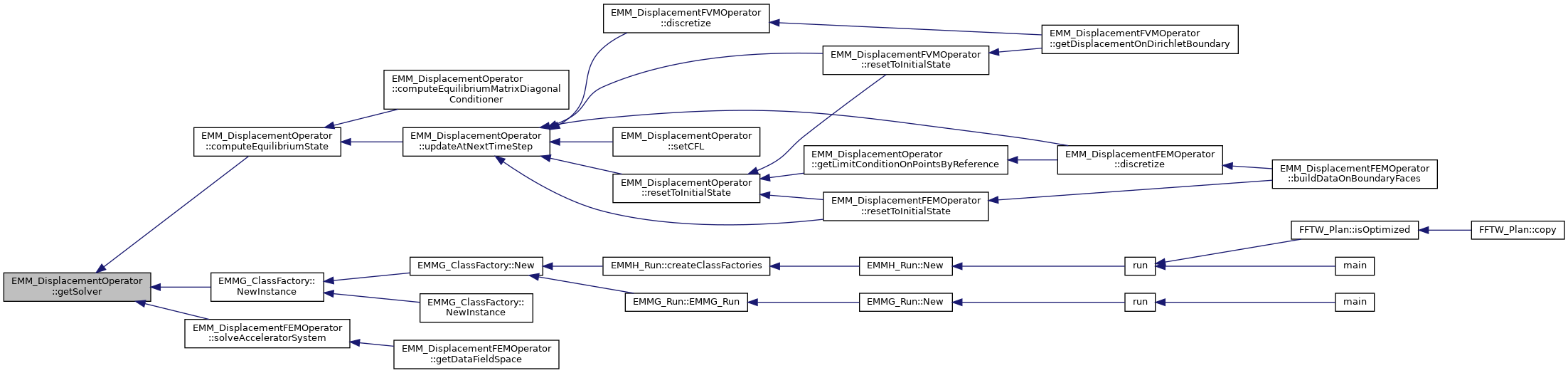
◆ getThread()
|
inlinestaticinherited |
get the profilier
- Returns
- the profiler
Referenced by MATH_MaskVector::add(), MATH_Vector::add(), addBoundaryElasticStress(), buildDataOnNeumannBoundaryFaces(), EMM_DisplacementFVMOperator::computeCineticEnergy(), EMM_DisplacementFVMOperator::computeElasticStress(), computeElasticStress(), EMM_DisplacementFVMOperator::computeElasticTensor(), computeElasticTensor(), EMM_StaticMagneticTensorOperator::computeEnergy(), EMM_CubicAnisotropyOperator::computeEnergy(), EMM_MagnetostrictionOperator::computeEnergy(), EMM_DisplacementOperator::computeEnergy(), EMM_AnisotropyOperator::computeEnergyWithMagneticExcitation(), EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), computeEquilibriumMatrixDiagonalConditioner(), EMM_FullExchangeOperator::computeMagneticExcitationField(), EMM_StaticMagnetostrictionOperator::computeMagneticExcitationField(), EMM_LinearAnisotropyOperator::computeMagneticExcitationField(), EMM_StaticMagneticTensorOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationField(), EMM_MinimalExchangeOperator::computeMagneticExcitationField(), EMM_AnisotropyOperator::computeMagneticExcitationField(), EMM_MagnetostrictionOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_AnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_DisplacementFVMOperator::computeMagneticStress(), computeMagneticStress(), EMM_OptimalTimeStep::computeOptimalTimeStep(), computeStressConstraintEnergy(), EMM_FullExchangeOperator::discretize(), EMM_MinimalExchangeOperator::discretize(), EMM_CondensedMassMatrix::discretize(), EMM_LinearAnisotropyOperator::discretize(), EMM_AnisotropyOperator::discretize(), EMM_DemagnetizedOperator::discretize(), EMMG_SLDemagnetizedOperator::discretize(), EMM_LandauLifschitzSystem::discretize(), MATH_Vector::divide(), MATH_MaskVector::dot(), MATH_Vector::dot(), EMM_4SymmetricTensors::doubleDot(), EMM_4Tensors::doubleDotCrossDoubleDotScalar(), EMM_4Tensors::doubleDotCrossProduct(), EMM_4Tensors::doubleDotCrossSquaredScalar(), EMM_4Tensors::doubleDotProduct(), MATH_Vector::init(), MATH_MaskVector::init(), EMM_LandauLifschitzODE_RK::integrateMagnetizationFieldAtTime(), EMM_DisplacementFVM_Interpolator::interpolateUAtVertices(), EMMG_SLDemagnetizedOperator::localAssembly(), EMM_DisplacementOperator::nullProjectionOnDirichletBoundary(), EMM_DisplacementOperator::periodicProjection(), EMM_2PackedSymmetricTensors::product(), EMM_CanonicalMassMatrix::product(), MATH_FullMatrix::product(), EMM_CondensedMassMatrix::product(), EMM_BlockMassMatrix::product(), MATH_MorseMatrix::product(), EMMG_SLDemagnetizedOperator::product(), EMM_DisplacementOperator::projectionOnDirichletBoundary(), EMM_LandauLifschitzSystem::resetOperatorsToInitialState(), EMM_DisplacementFVMOperator::setBoundaryFaceTypes(), FFTW_MultiDFTs::setFFT(), FFTW_MultiLevelsDFT::setFFT(), FFTW_MultiLevelsDFT::setLevels(), FFTW_MultiDFTs::setPlan(), FFTW_MultiLevelsDFT::setPlan(), EMM_CondensedMassMatrix::solve(), EMM_LandauLifschitzODE::solveODE(), EMM_4SymmetricTensors::squaredDoubleDot(), EMM_4Tensors::squaredDoubleDotCrossScalar(), EMM_4Tensors::squaredDoubleDotScalar(), EMM_CanonicalMassMatrix::symmetricDot(), EMM_CondensedMassMatrix::symmetricDot(), EMM_BlockMassMatrix::symmetricDot(), FFTW_Test::test(), MATH_SolverTest::test(), EMM_ODETest::testODE(), and EMM_Grid3D::updateLimitConditionOnPoints().

◆ getTimeIntegrationMethod()
|
inlineinherited |
get the time integration method for next time step
- Returns
- integration method in P1 | TE
References EMM_DisplacementOperator::mTimeIntegrationMethod.
◆ getTimeIntegrationOrder()
|
inlineinherited |
get the time integration order for new field
- Returns
- integration order in {1,2}
References EMM_DisplacementOperator::mTimeIntegrationOrder.
◆ getTimeStep()
|
inlineinherited |
get the time step for elasticty
- Returns
- the time step for elasticity
References EMM_DisplacementOperator::mDt.
◆ getTypeName()
|
inlinestaticinherited |
◆ getVelocity() [1/3]
|
inlineinherited |
get the velocity for writing
- Returns
- the velocity field
Referenced by EMM_DisplacementOperator::computeCineticEnergyAtTime(), EMM_DisplacementFVMOperator::discretize(), discretize(), EMM_DisplacementFVMOperator::getDataFieldSpace(), getDataFieldSpace(), EMM_DisplacementFVMOperator::resetToInitialState(), and EMM_DisplacementOperator::resetToInitialState().
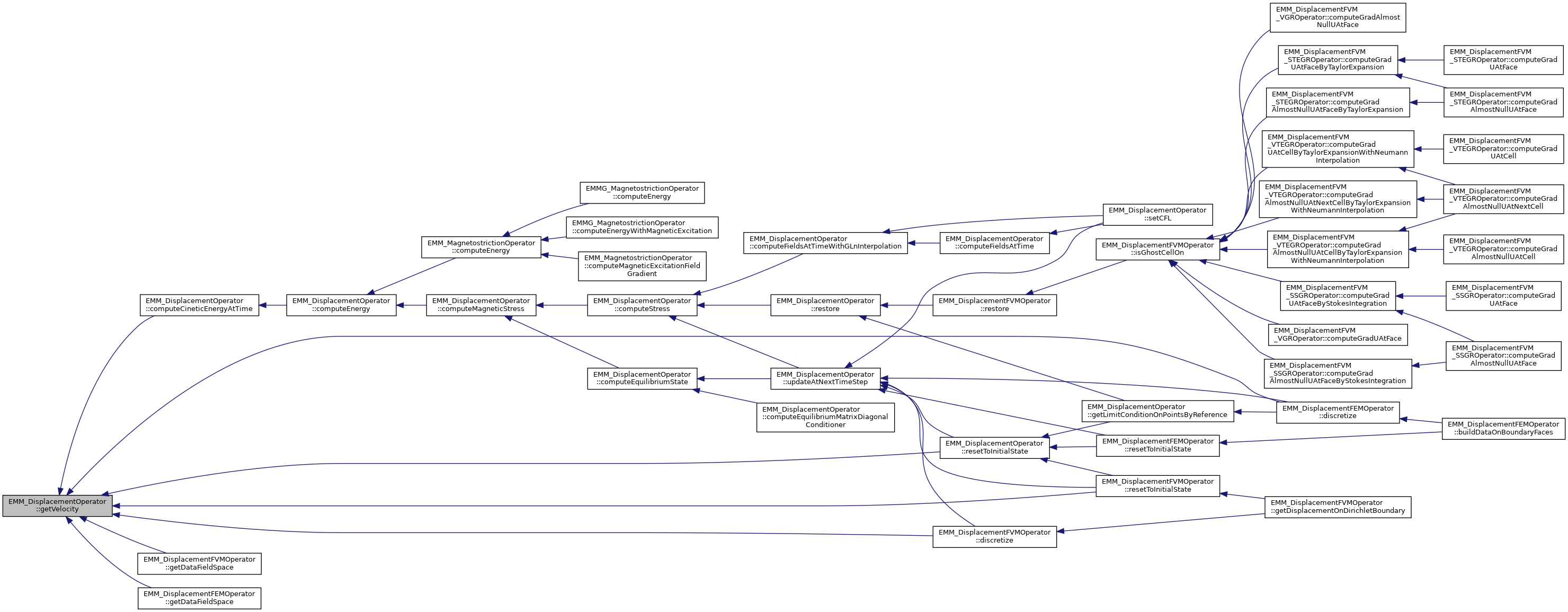
◆ getVelocity() [2/3]
|
inlineinherited |
get the velocity at time
- Parameters
-
t time to get velocity
References EMM_DisplacementOperator::isSteadyState().

◆ getVelocity() [3/3]
|
inlineinherited |
get the velocity at t for reading
- Returns
- the velocity field
◆ initializeEquilibriumSolver()
|
protectedvirtualinherited |
initialize the equilibrium solver
- Parameters
-
[in] U0 is the value of U on dirichlet points
- create the equilibrium matrix
- compute the preconditioner matrix
- compute the constant part of the affine elastic stree operator and store it in accelerator field
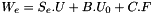
Reimplemented in EMM_DisplacementFVM_VIGROperator.
References EMM_DisplacementOperator::computeElasticStress(), EMM_DisplacementOperator::getAccelerator(), EMM_RealField::getDimension(), EMM_DisplacementOperator::getDisplacement(), EMM_RealField::getSize(), EMM_RealField::getValues(), EMM_RealField::initField(), EMM_DisplacementOperator::mEquilibriumMatrix, EMM_DisplacementOperator::NewEquilibriumMatrix(), EMM_RealField::NewInstance(), EMM_RealField::setDimension(), EMM_RealField::setSize(), EMM_DisplacementOperator::spaceProjection(), EMM_DisplacementOperator::spaceRelevant(), tDimension, tReal, tUIndex, and EMM_Object::Z.
Referenced by EMM_DisplacementOperator::computeEquilibriumMatrixDiagonalConditioner(), EMM_DisplacementFVM_VIGROperator::initializeEquilibriumSolver(), EMM_DisplacementOperator::restore(), and EMM_DisplacementOperator::updateAtNextTimeStep().
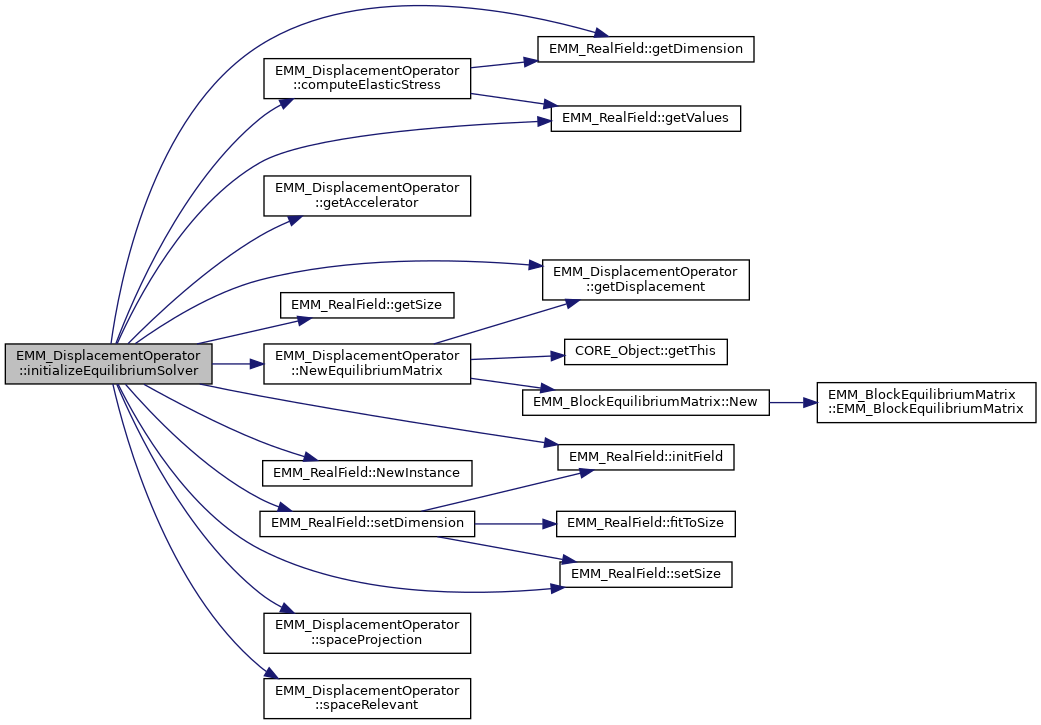
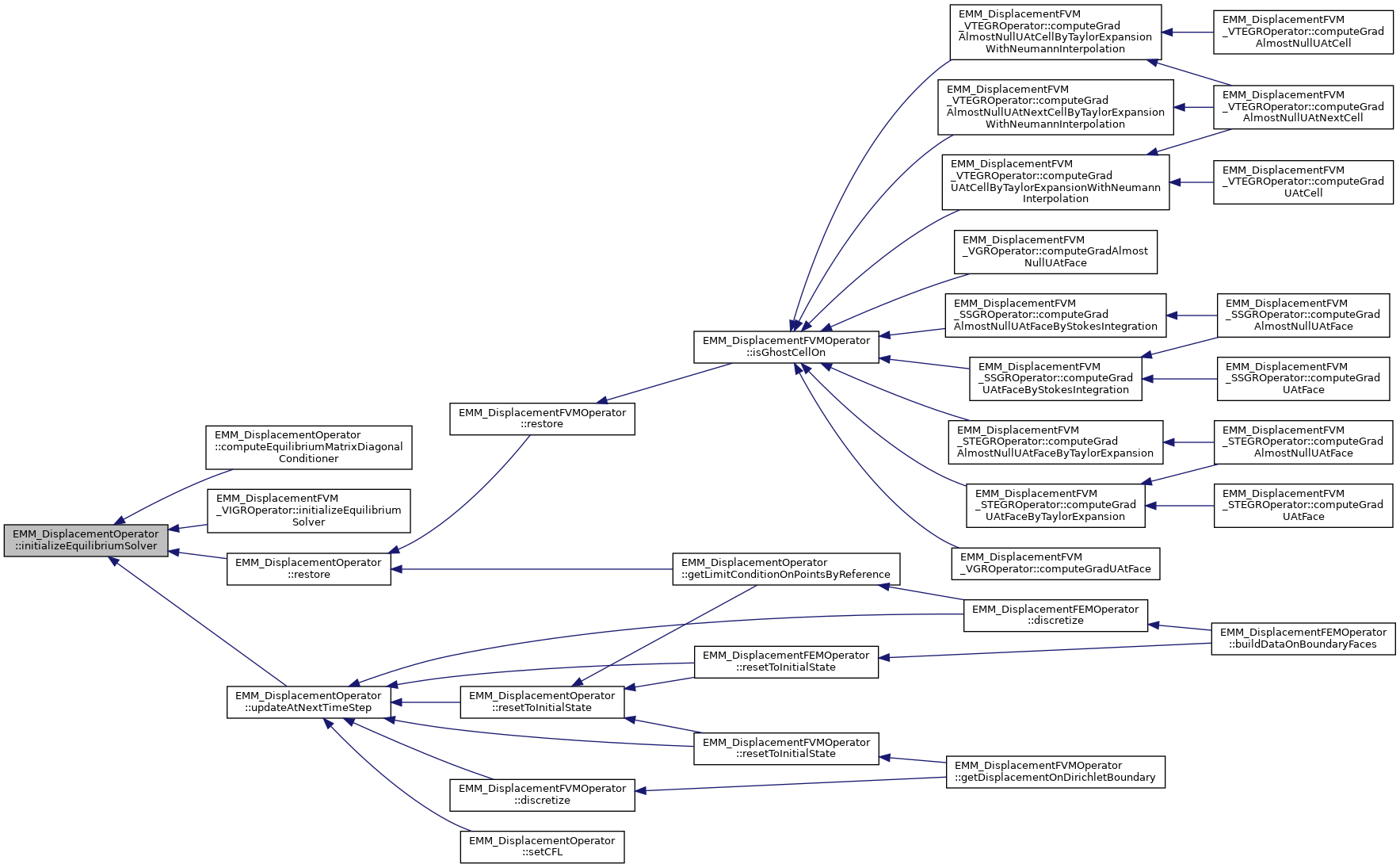
◆ is32Architecture()
|
inlinestaticinherited |
return true if the machine is a 32 bits machine
- Returns
- true is the computing is done in a 32 bits machine
References CORE_Object::pointer2String(), CORE_Object::printObjectsInMemory(), and tString.
Referenced by CORE_Test::testType().


◆ is64Architecture()
|
inlinestaticinherited |
return true if the machine is a 64 bits machine
- Returns
- true is the computing is done in a 64 bits machine
Referenced by EMM_VTK::getVTKType(), and CORE_Test::testType().
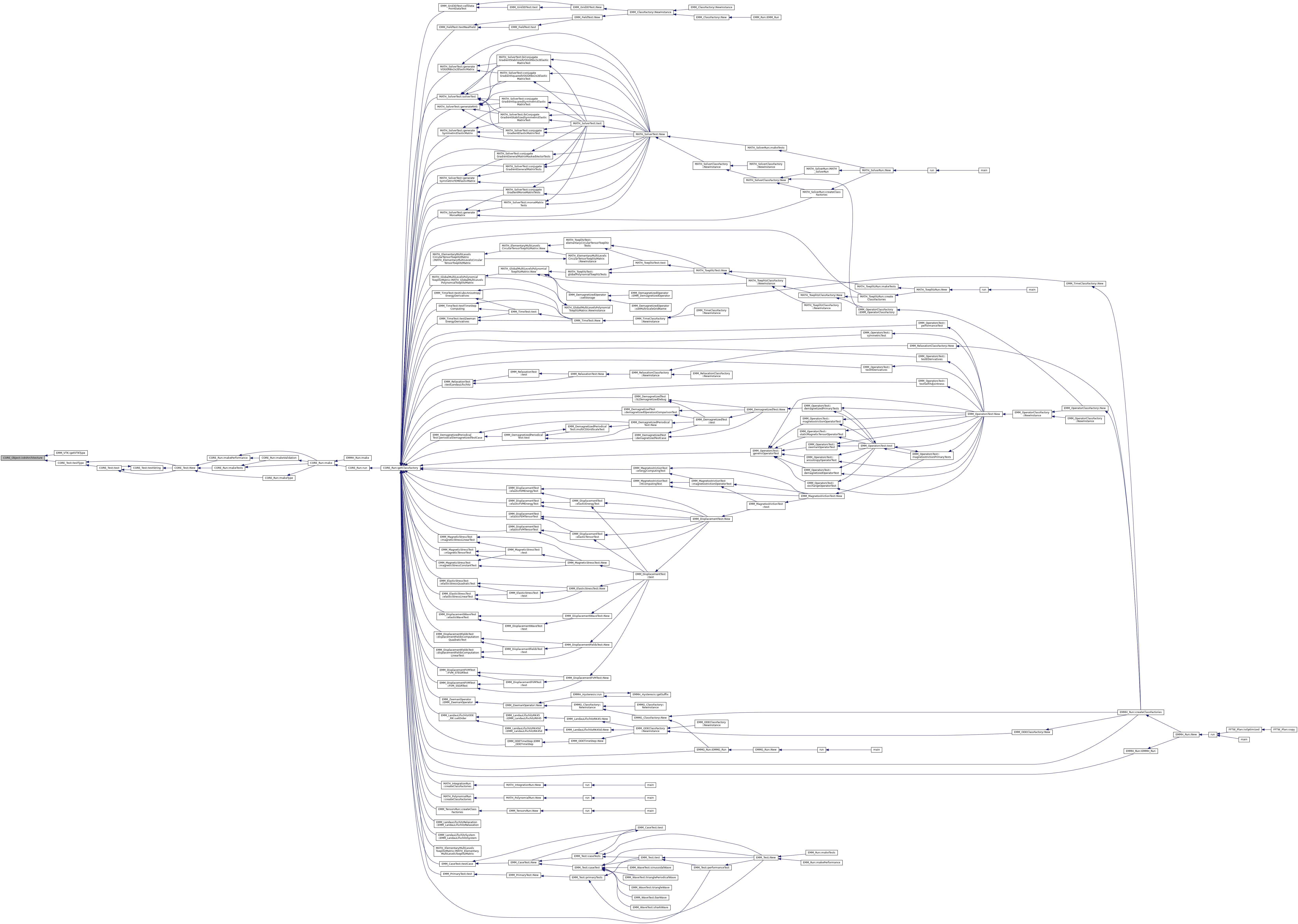
◆ isAffine()
|
inlinevirtualinherited |
return true if the operator is either constant or linear
- Returns
- true if the operator is either constant or linear
Implements EMM_Operator.
◆ isCubicVolume()
|
inlineinherited |
return the true if the element is cubic
- Returns
- true is all size of the volum is same
References EMM_Operator::mIsCubic.
Referenced by EMM_FullExchangeOperator::discretize(), and EMM_MinimalExchangeOperator::discretize().

◆ isEquilibriumMatrixReconditioned()
|
inlineinherited |
get if the equilibrium matrix is conditioned
- Returns
- true to recondition the equilibrium matrix
References EMM_DisplacementOperator::mIsEquilibriumMatrixConditioned.
Referenced by EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), and computeEquilibriumMatrixDiagonalConditioner().

◆ isEquilibriumState()
|
inlineinherited |
Referenced by EMM_DisplacementOperator::backup(), EMM_DisplacementOperator::computeEnergy(), EMM_DisplacementOperator::resetToInitialState(), EMM_DisplacementOperator::restore(), and EMM_DisplacementOperator::updateAtNextTimeStep().
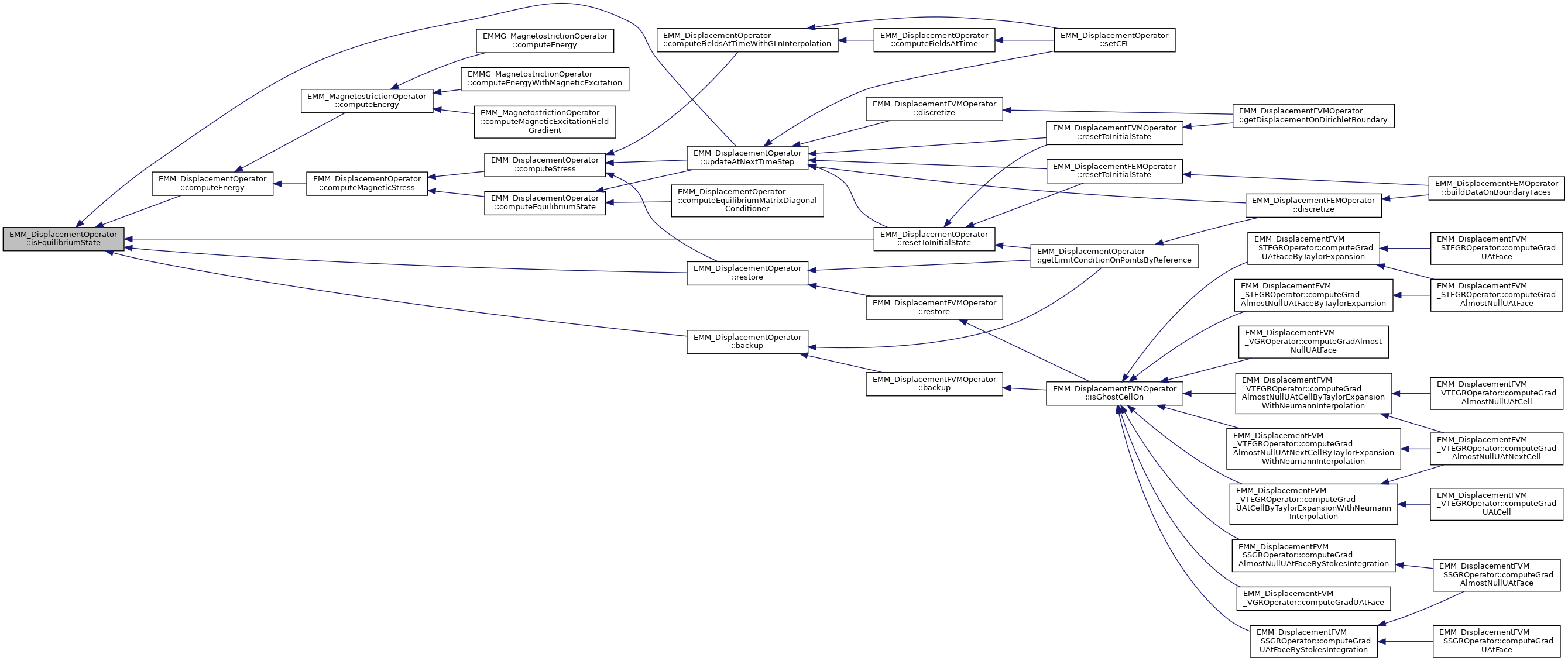
◆ isFrozenState()
|
inlineinherited |
Referenced by EMM_DisplacementOperator::backup(), and EMM_DisplacementOperator::updateAtNextTimeStep().
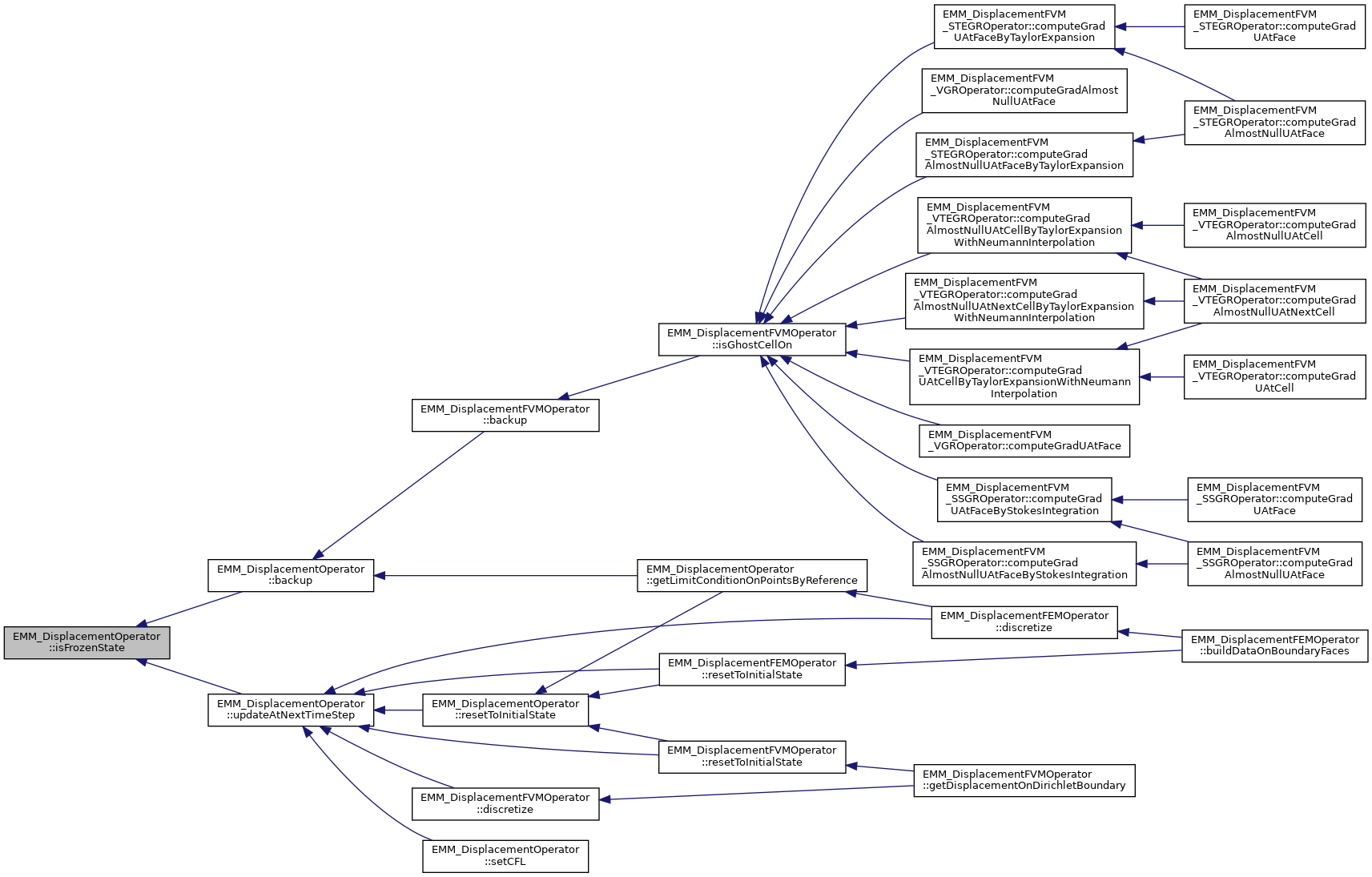
◆ isGradientComputationable()
|
inlinevirtualinherited |
return true if the gradient of the magnetic excitation is computationable
- Returns
- true if the the gradient of the magnetic excitation is computationable
Implements EMM_Operator.
◆ isInstanceOf() [1/2]
|
inlineinherited |
test if the clas T is an instance of this class
- Returns
- true if the object is an instance of T
References null.
Referenced by MATH_ToeplitzTest::toeplitzTest().

◆ isInstanceOf() [2/2]
test if the object is an instance of className
- Parameters
-
name name of the class
- Returns
- true if the object is an instance of class Name
References CORE_Object::getIdentityString().

◆ isMemoryChecked()
|
inlinestaticinherited |
get if the memory checking is used
- Returns
- true: if the memory checking is used.
References CORE_Object::getClassName(), CORE_Object::mIsMemoryTesting, and tString.
Referenced by main().


◆ isSteadyState()
|
inlineinherited |
Referenced by EMM_DisplacementOperator::computeFieldsAtTime(), EMM_DisplacementOperator::getDataFieldsNumber(), EMM_DisplacementOperator::getDisplacement(), and EMM_DisplacementOperator::getVelocity().
◆ NewEquilibriumMatrix()
|
virtualinherited |
create the equilibrium matrix
- Returns
- the equilibrium matrix
References EMM_DisplacementOperator::getDisplacement(), CORE_Object::getThis(), and EMM_BlockEquilibriumMatrix::New().
Referenced by EMM_DisplacementOperator::initializeEquilibriumSolver(), and EMM_DisplacementOperator::setCFL().

◆ NewMassMatrix()
|
virtual |
create the accelerator matrix
- Returns
- the accelerator matrix
References BLOCK_MASS_MATRIX, CANONICAL_MASS_MATRIX, CONDENSED_MASS_MATRIX, mMassMatrixType, EMM_BlockMassMatrix::New(), EMM_CanonicalMassMatrix::New(), and EMM_CondensedMassMatrix::New().
Referenced by discretize(), and getMassMatrixType().


◆ nullProjectionOnDirichletBoundary() [1/2]
|
inherited |
project the velocity to 0 on dirichlet boundary points
- Parameters
-
V the field
set V=0 on Dirichlet points; V must be defined on points (return an exception if not)
References EMM_RealField::getDimension(), EMM_RealField::getValues(), EMM_RealField::initField(), EMM_DisplacementOperator::mLimitConditionOnPoints, tDimension, tReal, and tUIndex.
Referenced by EMM_DisplacementOperator::getLimitConditionOnPointsByReference(), EMM_DisplacementOperator::projectionOnDirichletBoundary(), EMM_DisplacementOperator::resetToInitialState(), and spaceProjection().
◆ nullProjectionOnDirichletBoundary() [2/2]
|
inherited |
project the velocity to 0 on dirichlet boundary points
- Parameters
-
[in] nPoints : the number of points [in] dim : the dimension of each point [in,out] V : the values field defined on points
set V=0 on Dirichlet points; V must be defined on points (return an excepion if not)
References EMM_Grid3D::DIRICHLET_LIMIT_CONDITION, EMM_DisplacementOperator::getLimitConditionOnPoints(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tLimitCondition, tReal, tUIndex, and tUInteger.
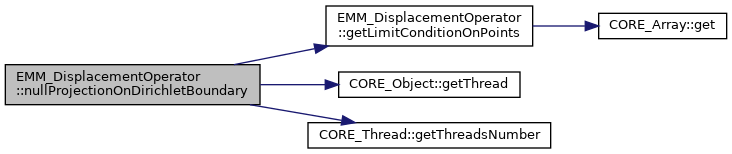
◆ out()
|
inlinestaticinherited |
get the output
- Returns
- the output stream
Referenced by EMM_Matter::adimensionize(), EMM_DisplacementFVMOperator::backup(), EMM_DisplacementOperator::backup(), MATH_ElementaryMultiLevelsToeplitzMatrix::buildSpectralVectorProjector(), EMM_Test::caseTest(), EMM_Test::caseTests(), EMM_MatterField::computeAnisotropyDirectionsField(), EMM_OptimalTimeStep::computeOptimalTimeStep(), MATH_MultiLevelsToeplitzMatrix::copy(), CORE_Exception::CORE_Exception(), EMM_MatterField::createAnisotropyOperator(), CORE_Run::createIO(), EMM_ElementaryTest::defaultBackupTest(), EMM_ElementaryTest::defaultTest(), MATH_MultiLevelsFFTToeplitzMatrix::diagonalize(), EMM_DisplacementFVMOperator::discretize(), EMM_MagnetostrictionOperator::discretize(), discretize(), EMM_4SymmetricTensors::doubleDot(), EMM_4Tensors::doubleDotCrossDoubleDotScalar(), EMM_TensorsTest::doubleDotCrossDoubleDotScalarTests(), EMM_4Tensors::doubleDotCrossProduct(), EMM_TensorsTest::doubleDotCrossProductTests(), EMM_4Tensors::doubleDotCrossSquaredScalar(), EMM_TensorsTest::doubleDotCrossSquaredScalarTests(), EMM_4Tensors::doubleDotProduct(), EMM_TensorsTest::doubleDotProductTests(), EMM_DisplacementWaveTest::elasticWaveTest(), EMM_Test::elementaryTests(), FFTW_Test::fftwTutorial(), MATH_IntegrationTest::gaussLegendreTest(), EMM_MagnetostrictionTest::HComputingTest(), EMM_DemagnetizedPeriodicalTest::HTest(), EMMH_HysteresisTest::hysteresisDefaultCycleTest(), EMM_TensorsTest::initializationTests(), EMM_MultiScaleGrid::initialize(), EMM_MultiScaleSDGrid::initialize(), EMM_MatterField::loadFromANIFile(), EMM_AnisotropyDirectionsField::loadFromFile(), EMM_Matter::loadFromFile(), EMM_Grid3D::loadFromGEOFile(), EMM_MatterField::loadFromLOCFile(), EMM_Array< tCellFlag >::loadFromStream(), EMM_Matter::loadFromStream(), EMM_Matter::loadMattersFromFile(), EMM_Run::loadSystemFromOptions(), EMM_ElementaryTest::magnetostrictionBackupTest(), CORE_Run::make(), EMMH_Run::makeHysteresis(), EMM_Run::makeRun(), CORE_Run::makeType(), EMM_ElementaryTest::optionsTest(), MATH_PolynomialTest::P4Tests(), EMM_Test::primaryTests(), EMM_LandauLifschitzSystem::printLog(), CORE_Run::printOptions(), EMM_2PackedSymmetricTensors::product(), EMMG_SLDemagnetizedOperator::projectionOnSpectralSpace(), CORE_Run::readOptionsFromCommandLine(), CORE_Test::readVectorTest(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_DisplacementFVMOperator::restore(), EMM_DisplacementOperator::restore(), EMM_Input::restoreBackup(), EMMH_Hysteresis::run(), EMM_Output::save(), EMM_AnisotropyDirectionsField::saveToFile(), EMM_MatterField::saveToFile(), EMM_Grid3D::saveToGEOFile(), CORE_IOTest::searchTest(), EMMH_Hysteresis::setInitialMagnetizationField(), MATH_MultiLevelsToeplitzMatrix::setLevels(), EMM_4SymmetricTensors::squaredDoubleDot(), EMM_4Tensors::squaredDoubleDotCrossScalar(), EMM_TensorsTest::squaredDoubleDotCrossScalarTests(), EMM_4Tensors::squaredDoubleDotScalar(), EMM_TensorsTest::squaredDoubleDotScalarTests(), EMM_TensorsTest::squaredDoubleDotTests(), EMM_MatterTest::testAdimensionize(), EMM_MatterTest::testANIFile(), CORE_Test::testComplex(), CORE_Test::testDateWeek(), FFTW_Test::testDFT(), EMM_MatterTest::testIO(), EMM_ODETest::testODE(), CORE_Test::testOut(), CORE_Test::testReal(), EMM_FieldTest::testRealArray(), EMM_Grid3DTest::testSegment(), EMM_Grid3DTest::testThinSheet(), CORE_Test::testTime(), CORE_Test::testType(), MATH_FullMatrix::toString(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().

◆ periodicProjection()
|
inherited |
make the periodic projection of the field V
- Parameters
-
periodicity :: periodcidcity projection nPoints number of points of each direction V field to project
V at slave point is set to V at master point
References EMM_Grid3D::GET_MASTER_PERIODIC_POINT(), EMM_RealField::getDimension(), EMM_DisplacementOperator::getLimitConditionOnPoints(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), EMM_RealField::getValues(), null, OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, EMM_Grid3D::SLAVE_LIMIT_CONDITION, tDimension, tLimitCondition, CORE_Integer::toString(), tReal, tUIndex, and tUInteger.
Referenced by EMM_DisplacementOperator::getLimitConditionOnPointsByReference(), EMM_DisplacementOperator::resetToInitialState(), and spaceRelevant().
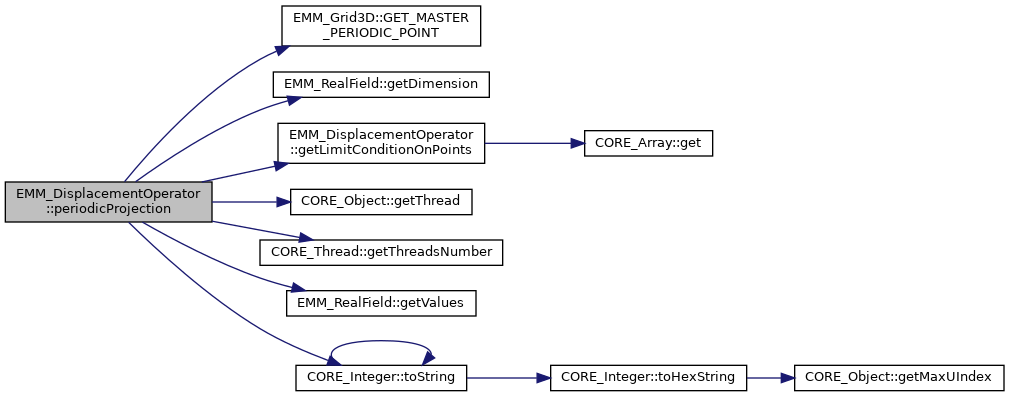

◆ pointer2String()
|
staticinherited |
return the string representation of a pointer
- Parameters
-
obj : oject to get the string pointer
- Returns
- the string pointer of the object
References tString.
Referenced by CORE_Object::CORE_Object(), CORE_Object::getIdentityString(), CORE_Object::getPointerAddress(), CORE_Object::is32Architecture(), and CORE_Object::~CORE_Object().

◆ printObjectsInMemory() [1/2]
|
staticinherited |
print object in memory
- Parameters
-
f : output to print the objects in memory
References CORE_Object::getIdentityString(), CORE_Object::getSharedPointer(), CORE_Object::mIsMemoryTesting, CORE_Object::mObjects, and tInteger.

◆ printObjectsInMemory() [2/2]
|
inlinestaticinherited |
print object in memory in the standart output
Referenced by CORE_Object::is32Architecture(), and main().
◆ projectionOnDirichletBoundary() [1/2]
|
inherited |
project the velocity to 0 on dirichlet boundary points
- Parameters
-
[in] V0 the field value on dirichlet points [out] V the field
set V=V0 on Dirichlet points; V must be defined on points (return an excepion if not)
References EMM_RealField::getDimension(), EMM_RealField::getSize(), EMM_RealField::getValues(), EMM_RealField::initField(), EMM_DisplacementOperator::mLimitConditionOnPoints, null, EMM_DisplacementOperator::nullProjectionOnDirichletBoundary(), tBoolean, tDimension, tReal, and tUIndex.
Referenced by EMM_DisplacementOperator::getLimitConditionOnPointsByReference(), and spaceProjection().
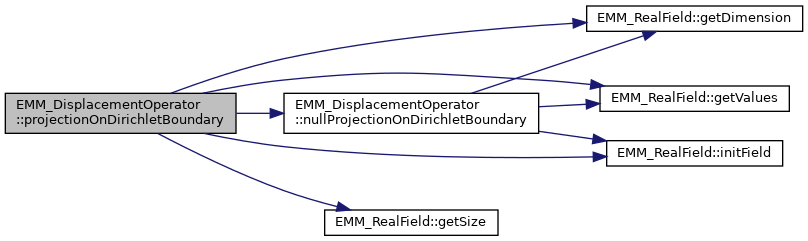

◆ projectionOnDirichletBoundary() [2/2]
|
inherited |
project the velocity to 0 on dirichlet boundary points
- Parameters
-
[in] nPoints the number of points [in] dim the dimension of each point [in] incV0 increment (either 0 or 1) of the values field on dirichlet points [in] V0 the values field on dirichlet points of size >=3 [in,out] V the values field defined on points
set V=V0 on Dirichlet points; V must be defined on points (return an excepion if not)
References EMM_Grid3D::DIRICHLET_LIMIT_CONDITION, EMM_DisplacementOperator::getLimitConditionOnPoints(), CORE_Object::getThread(), CORE_Thread::getThreadsNumber(), OMP_GET_THREAD_ID, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tDimension, tLimitCondition, tReal, tUIndex, and tUInteger.
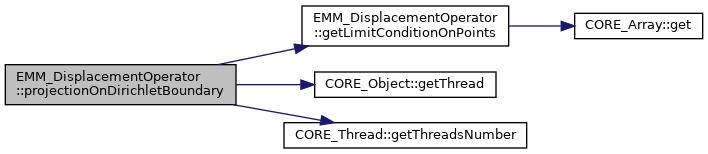
◆ resetOut()
|
inlinestaticinherited |
◆ resetThread()
|
inlinestaticinherited |
◆ resetToInitialState()
|
virtual |
reset the operator to initial state the operator
- Parameters
-
system the data to initialize the operator
- Returns
- true if it succeeds
- call EMM_DisplacementOperator::resetToInitialStep()
- recompute the accelerator vector at time 0
Reimplemented from EMM_DisplacementOperator.
References EMM_LandauLifschitzSystem::getMagnetizationField(), EMM_LandauLifschitzSystem::getSigma(), EMM_DisplacementOperator::resetToInitialState(), tBoolean, and EMM_DisplacementOperator::updateAtNextTimeStep().
Referenced by buildDataOnBoundaryFaces().
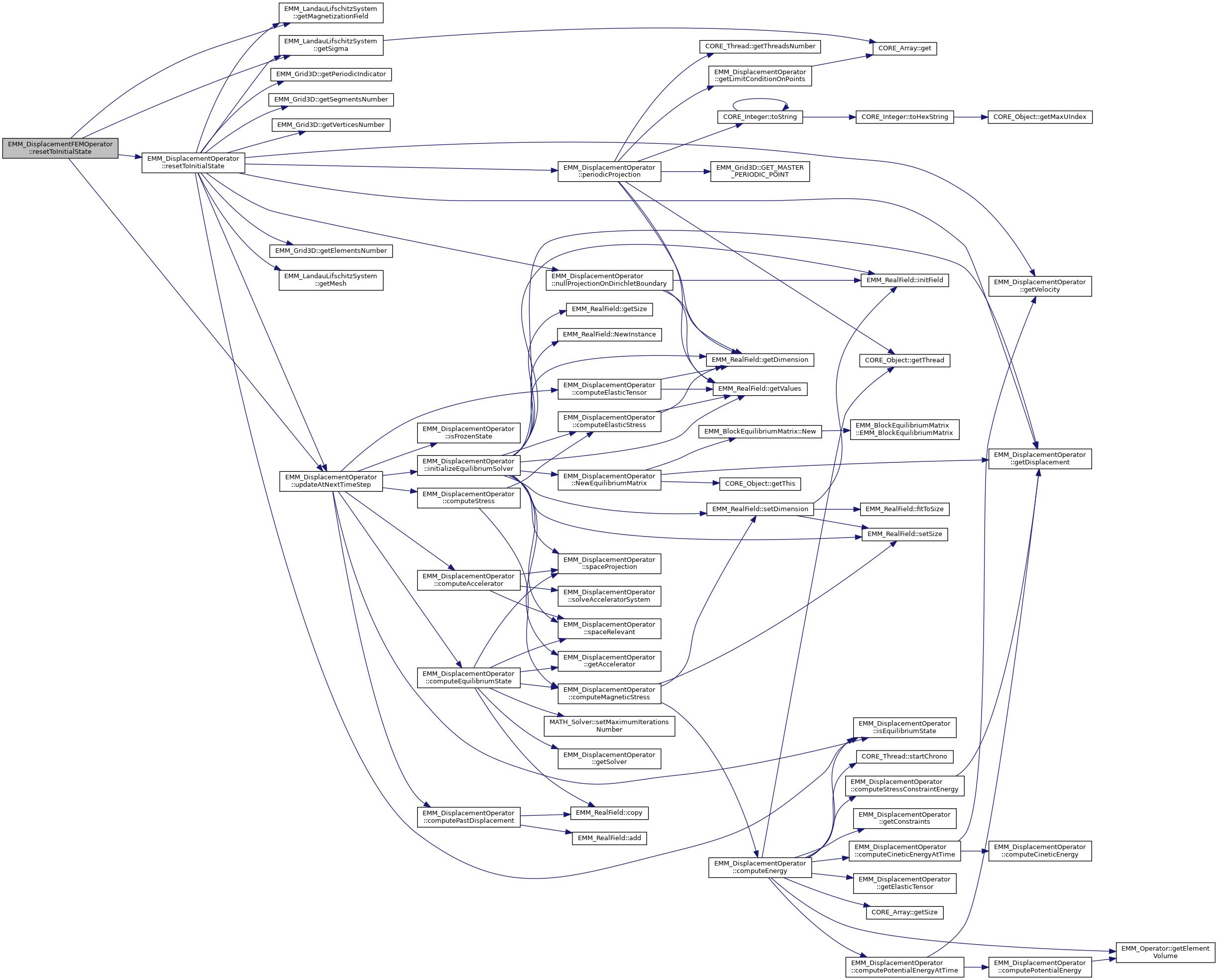

◆ restore()
|
virtualinherited |
restore the operator data from file(s)
- Parameters
-
system : general data to restore the operator prefix : common prefix of the saving files suffix : common suffix of the saving files ext : common extension of the saving files
- Returns
- if the restoring of the displacament & velocity field have succeeds
It restore the state from :
- the current time step in {prefix}_dt_{suffix}.{ext}
- U at previous time step in {prefix}_Unm1_{suffix}.{ext}
- U at current time step in {prefix}_Un_{suffix}.{ext}
- V at current time step in {prefix}_Vn_{suffix}.{ext}
- dV/dt at current time step in {prefix}_Acc_{suffx}.{ext}
Reimplemented from EMM_Operator.
Reimplemented in EMM_DisplacementFVMOperator.
References EMM_DisplacementOperator::computeAccelerator(), EMM_DisplacementOperator::computeElasticTensor(), EMM_DisplacementOperator::computeStress(), EMM_LandauLifschitzSystem::getMagnetizationField(), EMM_LandauLifschitzSystem::getSigma(), EMM_DisplacementOperator::initializeEquilibriumSolver(), EMM_DisplacementOperator::isEquilibriumState(), EMM_DisplacementOperator::mAccelerator, EMM_DisplacementOperator::mDt, EMM_DisplacementOperator::mEpsilonUt, EMM_DisplacementOperator::mKappa, EMM_DisplacementOperator::mTimeIntegrationMethod, EMM_DisplacementOperator::mUn, EMM_DisplacementOperator::mUnm1, EMM_DisplacementOperator::mVn, CORE_Object::out(), CORE_Out::println(), tBoolean, EMM_DisplacementOperator::TE, CORE_Real::toString(), and tString.
Referenced by EMM_DisplacementOperator::getLimitConditionOnPointsByReference(), and EMM_DisplacementFVMOperator::restore().
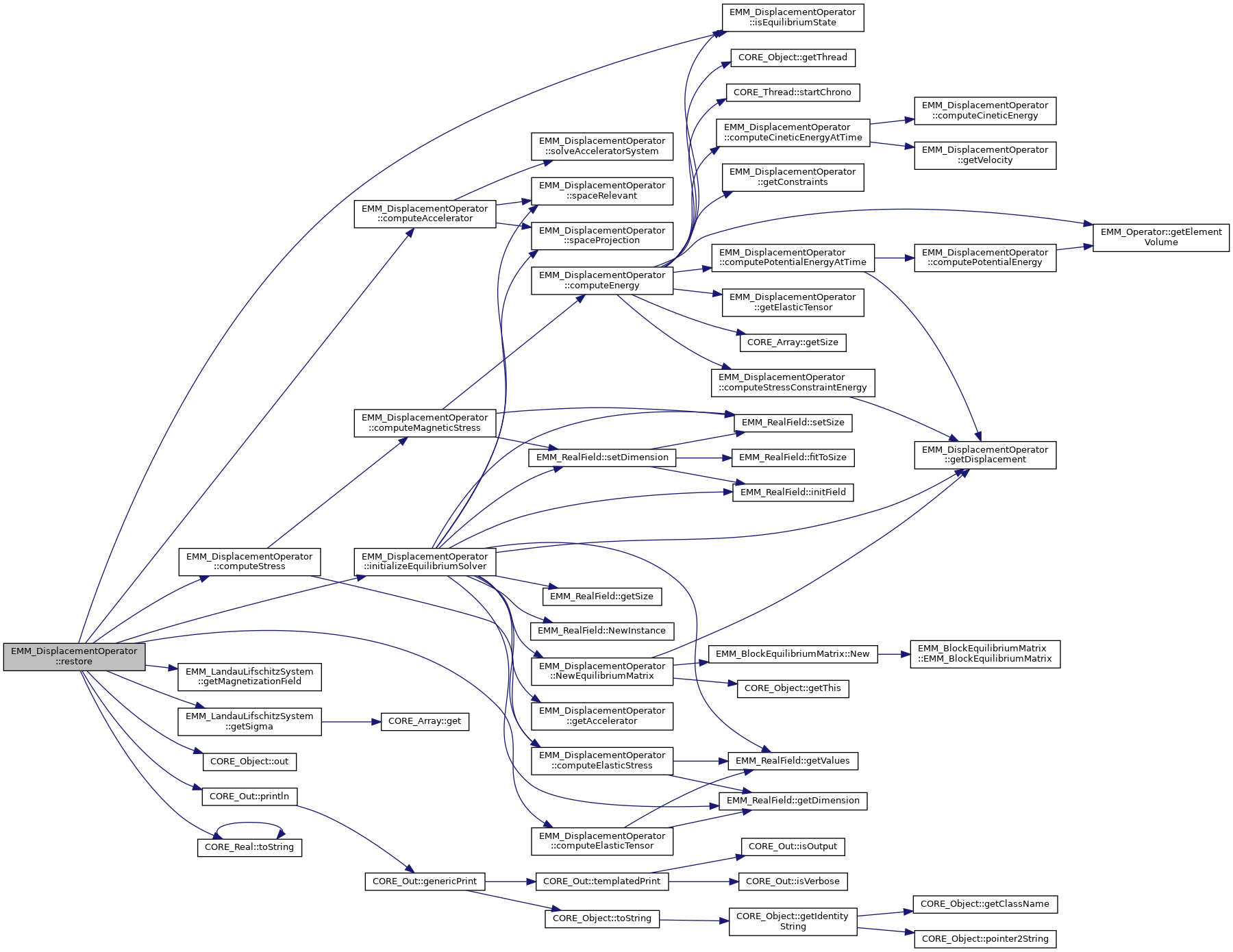
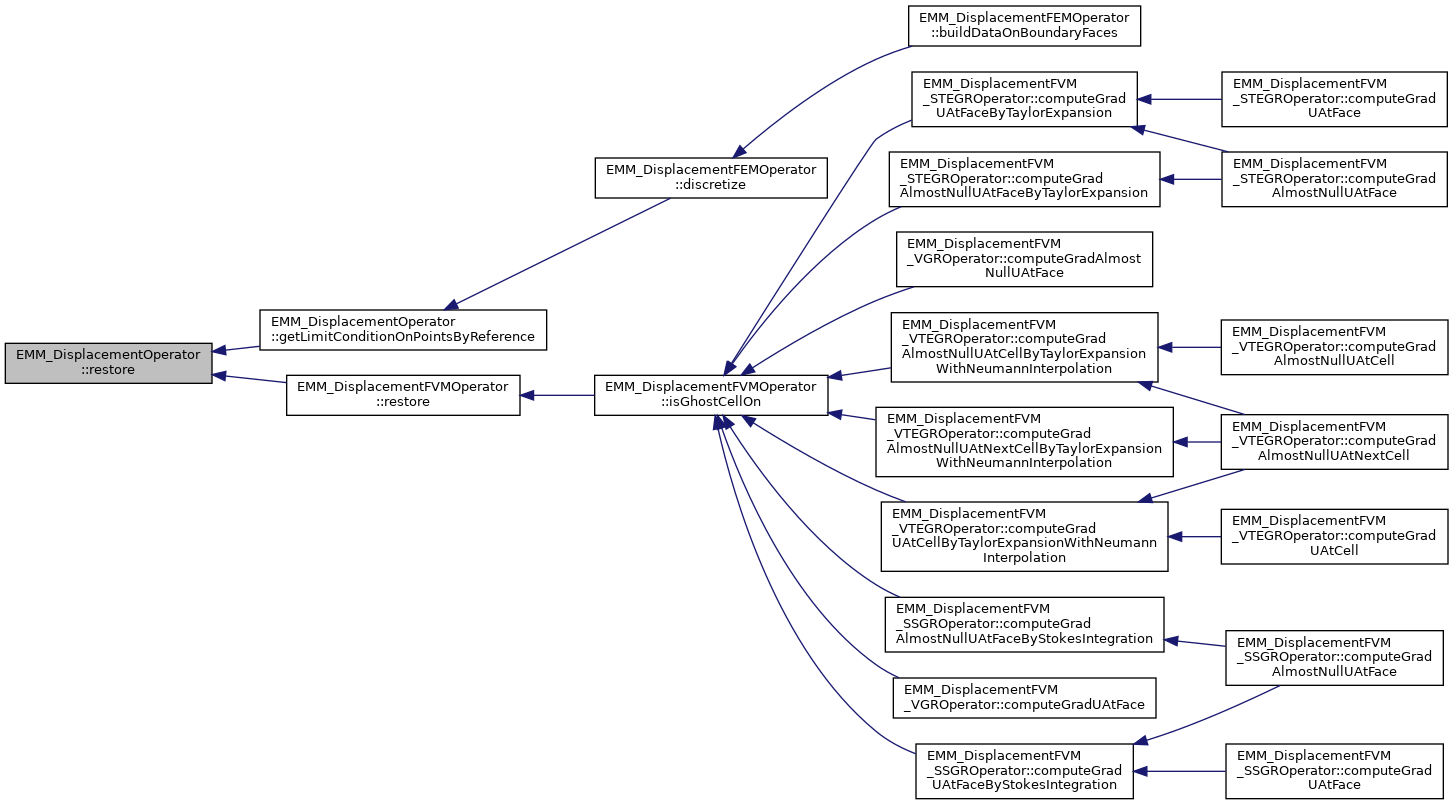
◆ setCFL()
|
inlineinherited |
set the cfl for computing the initial time step
- Parameters
-
cfl initial time step
References EMM_DisplacementOperator::computeAccelerator(), EMM_DisplacementOperator::computeFieldsAtTime(), EMM_DisplacementOperator::computeFieldsAtTimeWithGL1Interpolation(), EMM_DisplacementOperator::computeFieldsAtTimeWithGLnInterpolation(), EMM_DisplacementOperator::computeFieldsAtTimeWithTE1(), EMM_DisplacementOperator::computeFieldsAtTimeWithTE2(), EMM_DisplacementOperator::computePastDisplacement(), EMM_DisplacementOperator::NewEquilibriumMatrix(), EMM_DisplacementOperator::solveAcceleratorSystem(), EMM_DisplacementOperator::spaceProjection(), EMM_DisplacementOperator::spaceRelevant(), tBoolean, tFlag, tReal, and EMM_DisplacementOperator::updateAtNextTimeStep().
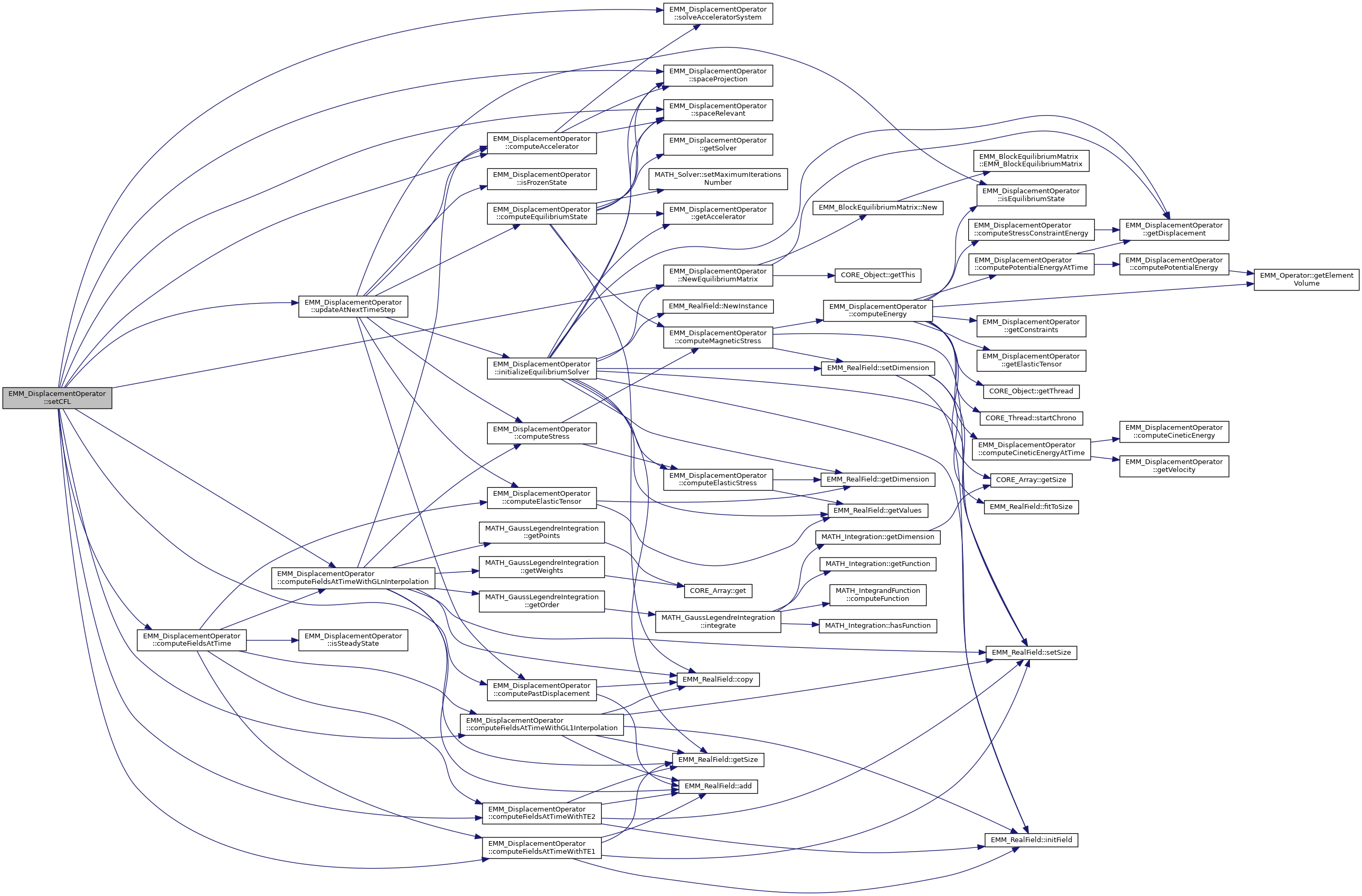
◆ setConstraints() [1/4]
|
inlineinherited |
set constraints from file defined on points
- Parameters
-
C constraints faces in bit : 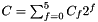
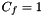 if face f is constrainted
if face f is constrainted dataFile : file which contains the constraints field defined on points
Referenced by EMMG_ClassFactory::NewInstance().

◆ setConstraints() [2/4]
|
inlineinherited |
set constraints field
- Parameters
-
C constraint faces in bit : 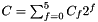
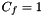 if face f is constrainted
if face f is constrainted data : uniform data for constraints
References EMM_RealField::setValue().

◆ setConstraints() [3/4]
|
inlineinherited |
set initial constriants field
- Parameters
-
C constraint faces in bit : 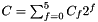
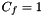 if face f is constrainted
if face f is constrainted C0 x-coordinate of constraint C1 y-coordinate of constraint C2 z-coordinate of constraint
References EMM_RealField::initField().

◆ setConstraints() [4/4]
|
inlineinherited |
set constraints
- Parameters
-
C constraint faces in bit : 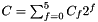
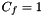 if face f is constrainted
if face f is constrainted data constraints field
◆ setDisplacement() [1/2]
|
inlineinherited |
set the displacement field
- Parameters
-
u : is the displacement field defined ob points
◆ setDisplacement() [2/2]
|
inlineinherited |
set the displacement field to an uniform vector defied on points
- Parameters
-
Ux uniform value of the field on the x-direction Uy uniform value of the field on the y-direction Uz uniform value of the field on the z-direction
◆ setElasticityState()
|
inlineinherited |
set the elasticity state
- Parameters
-
v the elasticity state eithet equilibrium | steady | unsteady
Referenced by EMMG_ClassFactory::NewInstance().

◆ setInitialDisplacement() [1/4]
|
inlineinherited |
set initial displacement field.
- Parameters
-
scale : the scale factor of the file dataFile : file which contains the displacement field defined on points
Referenced by EMMG_ClassFactory::NewInstance().

◆ setInitialDisplacement() [2/4]
|
inlineinherited |
set initial displacement field
- Parameters
-
data : uniform data for displacement
References EMM_RealField::setValue().

◆ setInitialDisplacement() [3/4]
|
inlineinherited |
set initial displacement field
- Parameters
-
U0 x-coordinate of displacement U1 y-coordinate of displacement U2 z-coordinate of displacement
References EMM_RealField::initField().

◆ setInitialDisplacement() [4/4]
|
inlineinherited |
set initial displacement field
- Parameters
-
data : data for displacement
◆ setInitialVelocity() [1/4]
|
inlineinherited |
set initial velocity field
- Parameters
-
scale scale of the file dataFile : file which contains the velocity field defined on points
Referenced by EMMG_ClassFactory::NewInstance().

◆ setInitialVelocity() [2/4]
|
inlineinherited |
set initial velocity field
- Parameters
-
data velocity field
◆ setInitialVelocity() [3/4]
|
inlineinherited |
set initial velocity field
- Parameters
-
data : uniform data for velocity
References EMM_RealField::setValue().

◆ setInitialVelocity() [4/4]
|
inlineinherited |
set initial velocity field
- Parameters
-
V0 x-coordinate of velocity V1 y-coordinate of velocity V2 z-coordinate of velocity
References EMM_RealField::initField().

◆ setIsEquilibriumMatrixReconditioned()
|
inlineinherited |
set to true if the equilibrium matrix is conditioned
- Parameters
-
c true to recondition the equilibrium matrix
◆ setIsMemoryChecked()
|
inlinestaticinherited |
set if the memory checking is used
- Parameters
-
v : true to check memory
Referenced by main().

◆ setLimitConditionOnPoints() [1/2]
|
inlineinherited |
set the limit condition each point is set to
- Parameters
-
lc the limit condition value for all points of the mesh. Interior point are ignored (0) - NO_LIMIT_CONDITION for all interior points or not magnetized point
- DIRICHLET_LIMIT_CONDITION for all points on Dirichlet boundary
- NEUMANN_LIMIT_CONDITION for all points on Neumann boundary
Referenced by EMMG_ClassFactory::NewInstance().

◆ setLimitConditionOnPoints() [2/2]
|
inlineinherited |
set the limit condition to all points
- Parameters
-
lc the limit condition value for all points of the mesh. Interiror point are ignored (0) - NO_LIMIT_CONDITION for all interior points or not magnetized point
- DIRICHLET_LIMIT_CONDITION for all points on Dirichlet boundary
- NEUMANN_LIMIT_CONDITION for all points on Neumann boundary
◆ setMassMatrixType()
|
inline |
set the mass matrix type
- Parameters
-
t : the mass matrix type CANONICAL,BLOCK,CONDENSED
◆ setOut()
|
inlinestaticinherited |
◆ setSolver() [1/2]
|
virtualinherited |
set the solver
- Parameters
-
solverName name of the solver which can be either : - CG or
- biCGStab or
- empty
If empty biCGStab is used only for FVM displacement with equilibrium state
Reimplemented in EMM_DisplacementFVMOperator.
References tString.
Referenced by EMM_DisplacementOperator::getAccelerator(), EMMG_ClassFactory::NewInstance(), and EMM_DisplacementFVMOperator::setSolver().

◆ setSolver() [2/2]
|
inlineinherited |
set the solver
- Parameters
-
solver : the solver
◆ setThis()
|
inlineprotectedinherited |
set this weak shared pointer called toDoAfterThis setting method
- Parameters
-
p : shared pointer of the class This
References CORE_Object::toDoAfterThisSetting().

◆ setThread()
|
inlinestaticinherited |
set the thread
- Parameters
-
thread the shared pointer to the thread
References null.
Referenced by EMM_Run::EMM_Run(), EMM_TensorsRun::EMM_TensorsRun(), and MATH_SolverRun::MATH_SolverRun().
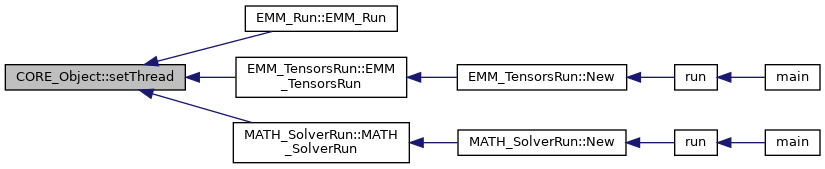
◆ setTimeIntegrationMethod()
|
inlineinherited |
set the time integration method for new field
- Parameters
-
m integration method in P1 | TE
Referenced by EMMG_ClassFactory::NewInstance().

◆ setTimeIntegrationOrder()
|
inlineinherited |
set the time integration order for new field
- Parameters
-
o integration ordre in {1,2}
Referenced by EMMG_ClassFactory::NewInstance().

◆ setVelocity() [1/2]
|
inlineinherited |
set the velocity of dicplacement defined on points
- Parameters
-
v : is the displacement velocity field
◆ setVelocity() [2/2]
|
inlineinherited |
set the displacement velocity field to an uniform vector defined on points
- Parameters
-
Vx uniform value of the field on the x-direction Vy uniform value of the field on the y-direction Vz uniform value of the field on the z-direction
◆ solveAcceleratorSystem()
|
protectedvirtual |
solve the velocity form the accelerator matrix : M.X=V V:=X
- Parameters
-
V - input : the total stress
- output : the accelerator
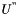
- Returns
- true if the solving succeeds
M is the mass matrix
Implements EMM_DisplacementOperator.
References EMM_DisplacementOperator::getSolver(), mMassMatrix, and tBoolean.
Referenced by getDataFieldSpace().


◆ SP_OBJECT()
|
private |
◆ spaceProjection() [1/2]
|
protectedvirtual |
make the projection of the vector B into the solving linear space
- Parameters
-
[out] V field to project in linear solving space
V is set to 0 on all dirichlet points
Implements EMM_DisplacementOperator.
References EMM_DisplacementOperator::nullProjectionOnDirichletBoundary().
Referenced by getDataFieldSpace().


◆ spaceProjection() [2/2]
|
protectedvirtual |
make the projection of the vector B into the solving linear space
- Parameters
-
[in] V0 :orthogonal vector of the linear solving space [out] V : field to project in linear solving space
V is set to V0 on all dirichlet points
Implements EMM_DisplacementOperator.
References EMM_DisplacementOperator::projectionOnDirichletBoundary().
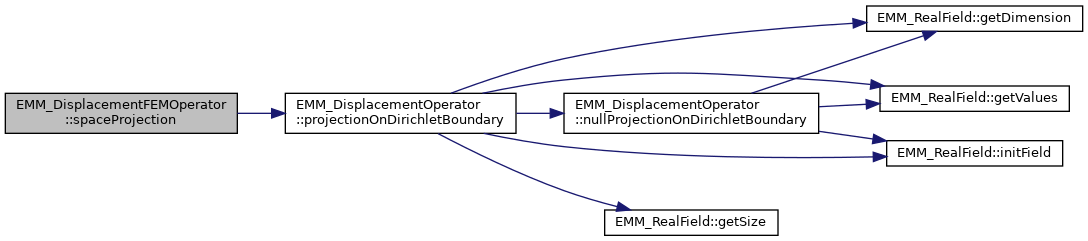
◆ spaceRelevant()
|
protectedvirtual |
make the rebuild of the vector V from the solving space.
- Parameters
-
V the vector to rebuild from the solving space
V at slave periodical point is set to the value of V at the master periodical point
Implements EMM_DisplacementOperator.
References getPeriodicIndicator(), mMassMatrix, and EMM_DisplacementOperator::periodicProjection().
Referenced by getDataFieldSpace().
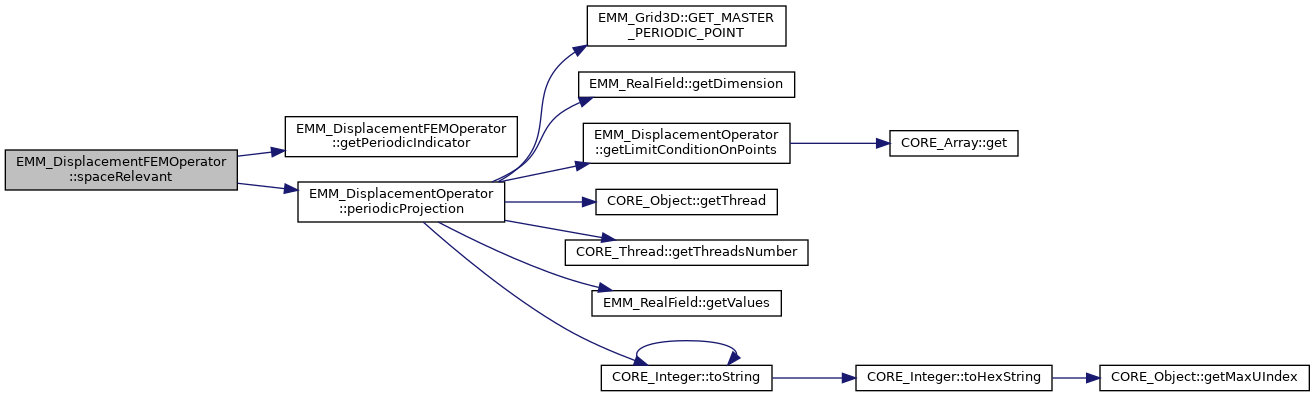

◆ toDoAfterThisSetting()
|
inlineprotectedvirtualinherited |
method called after the setting of the shared pointer this method can only be called once.
Reimplemented from EMM_Object.
Reimplemented in EMM_DisplacementFVMOperator.
References EMM_Object::toDoAfterThisSetting().
Referenced by EMM_DisplacementFVMOperator::toDoAfterThisSetting().


◆ toString()
|
inlinevirtual |
turn the martix into string
Reimplemented from EMM_DisplacementOperator.
Referenced by discretize().

◆ updateAtNextTimeStep()
|
virtualinherited |
update the data of operator at next time step
- Parameters
-
dt the time step sigma the magnetized weight of each cell Mt the magnetization field at each point at next time step
- Returns
- true if the updating of the operator has succeeded if (dt==0) the function is called after discretization during the relaxation process
Implements EMM_Operator.
References EMM_DisplacementOperator::computeAccelerator(), EMM_DisplacementOperator::computeElasticTensor(), EMM_DisplacementOperator::computeEquilibriumState(), EMM_DisplacementOperator::computePastDisplacement(), EMM_DisplacementOperator::computeStress(), EMM_DisplacementOperator::initializeEquilibriumSolver(), EMM_DisplacementOperator::isEquilibriumState(), EMM_DisplacementOperator::isFrozenState(), EMM_DisplacementOperator::mAccelerator, EMM_DisplacementOperator::mDt, EMM_DisplacementOperator::mEpsilonUt, EMM_DisplacementOperator::mKappa, EMM_DisplacementOperator::mTimeIntegrationMethod, EMM_DisplacementOperator::mTimeIntegrationOrder, EMM_DisplacementOperator::mUn, EMM_DisplacementOperator::mUnm1, EMM_DisplacementOperator::mUt, EMM_DisplacementOperator::mVn, EMM_DisplacementOperator::mVt, tBoolean, and EMM_DisplacementOperator::TE.
Referenced by EMM_DisplacementFVMOperator::discretize(), discretize(), EMM_DisplacementFVMOperator::resetToInitialState(), resetToInitialState(), EMM_DisplacementOperator::resetToInitialState(), and EMM_DisplacementOperator::setCFL().
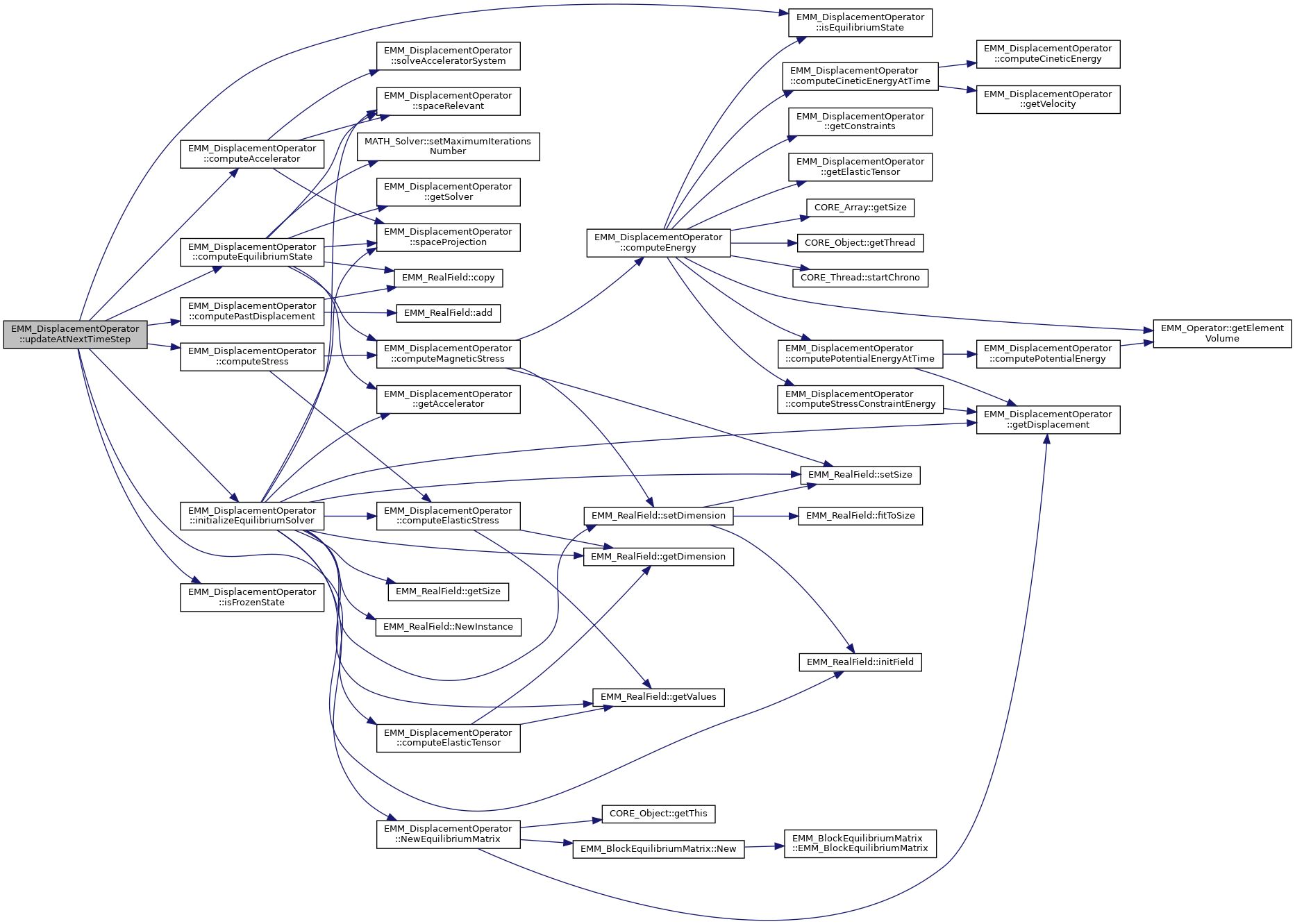
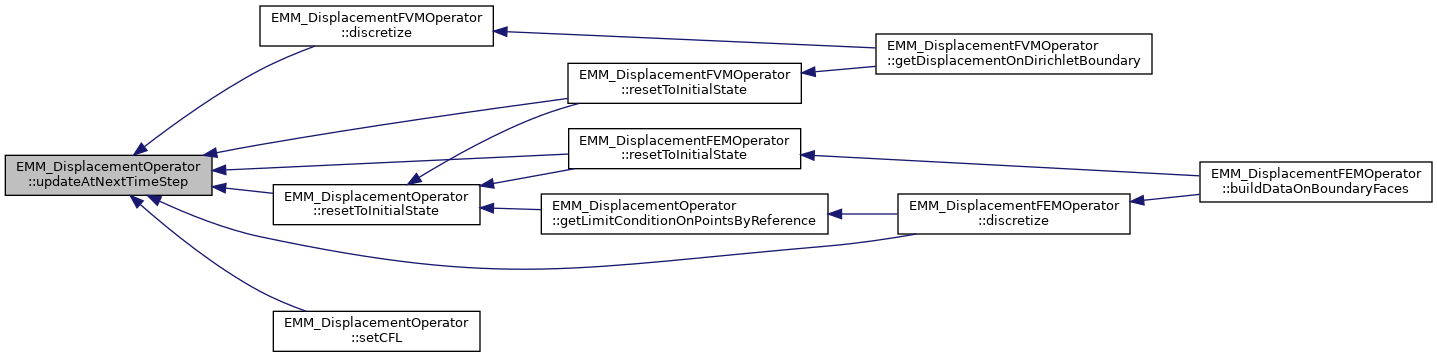
Member Data Documentation
◆ BLOCK_MASS_MATRIX
|
static |
mass matrix whose each element is a digonal matrixof size 3
Referenced by EMM_DisplacementFEMOperator(), and NewMassMatrix().
◆ CANONICAL_MASS_MATRIX
|
static |
mass matrix whose each element is real
Referenced by NewMassMatrix().
◆ CONDENSED_MASS_MATRIX
|
static |
mass matrix is diagonal
Referenced by NewMassMatrix().
◆ EQUILIBRIUM_STATE
|
staticinherited |
Referenced by EMMG_ClassFactory::NewInstance().
◆ FROZEN_STATE
|
staticinherited |
Referenced by EMMG_ClassFactory::NewInstance().
◆ Gamma
|
staticinherited |
◆ INT_GRAD_PHI
|
staticprivate |
Referenced by computeElasticTensor(), and computeMagneticStress().
◆ INT_GRAD_PHI_FACTOR
|
staticprivate |
Referenced by computeElasticTensor(), and computeMagneticStress().
◆ mMassMatrix
|
private |
Referenced by computeCineticEnergy(), discretize(), solveAcceleratorSystem(), and spaceRelevant().
◆ mMassMatrixType
|
private |
Referenced by EMM_DisplacementFEMOperator(), getMassMatrixType(), and NewMassMatrix().
◆ Mu0
|
staticinherited |
Referenced by EMM_MatterField::adimensionize(), EMM_MagnetostrictionOperator::adimensionize(), EMM_Matter::adimensionize(), EMM_CubicAnisotropyOperator::ComputeMagneticExcitation(), EMM_CubicAnisotropyOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_CubicAnisotropyOperator::ComputeMagneticExcitationGradient(), EMM_Test::createMatters(), EMM_MatterField::getElasticTensorAdimensionizedParameter(), and EMM_MatterTest::testAdimensionize().
◆ NULL_VALUE
|
staticinherited |
Referenced by EMM_DisplacementFVM_VOGGROperator::computeGradAlmostNullUAtCellByOstrogradskiGreenIntegration(), EMM_DisplacementFVM_VTEGROperator::computeGradAlmostNullUAtCellByTaylorExpansionWithNeumannInterpolation(), EMM_DisplacementFVM_SSGROperator::computeGradAlmostNullUAtFaceByStokesIntegration(), EMM_DisplacementFVM_VOGGROperator::computeGradAlmostNullUAtNextCellByOstrogradskiGreenIntegration(), EMM_DisplacementFVM_VTEGROperator::computeGradUAtCellByTaylorExpansionWithNeumannInterpolation(), EMM_DisplacementFVM_VGROperator::computeGradUAtFace(), EMM_DisplacementFVM_SSGROperator::computeGradUAtFaceByStokesIntegration(), EMM_DisplacementFVM_STEGROperator::computeGradUAtFaceByTaylorExpansion(), EMM_DisplacementFVM_Interpolator::interpolateUAtEdge(), and EMM_DisplacementFVM_Interpolator::interpolateUAtVertices().
◆ P1
|
staticinherited |
◆ TE
|
staticinherited |
Referenced by EMM_DisplacementOperator::backup(), EMM_DisplacementOperator::computeFieldsAtTime(), EMM_DisplacementOperator::EMM_DisplacementOperator(), EMMG_ClassFactory::NewInstance(), EMM_DisplacementOperator::restore(), EMM_DisplacementFieldsTest::test(), and EMM_DisplacementOperator::updateAtNextTimeStep().
◆ UNSTEADY_STATE
|
staticinherited |
Referenced by EMM_DisplacementOperator::EMM_DisplacementOperator(), and EMMG_ClassFactory::NewInstance().
◆ X
|
staticinherited |
◆ Y
|
staticinherited |
Referenced by EMMG_SLSDXPeriodicMultiScale::computeMultiGridExcitationField(), EMMG_RealField::fitToSize(), EMM_MassMatrix::getElementVolume(), EMM_CanonicalMassMatrix::isSymmetric(), EMM_BlockMassMatrix::product(), EMM_CondensedMassMatrix::product(), EMM_RealField::setValue(), EMM_CanonicalMassMatrix::solve(), EMM_BlockMassMatrix::solve(), EMM_BlockMassMatrix::toString(), and EMMG_RealField::wedge().
◆ Z
|
staticinherited |
The documentation for this class was generated from the following files:
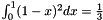
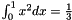
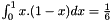
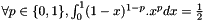
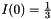
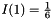
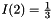
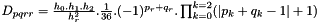
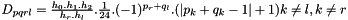


 1.8.13
1.8.13