This class describes the building of fields on multiscale shift dioptic grids initialized by the initialize() method. More...
#include <EMM_MultiScaleSDGrid.h>
Public Member Functions | |
| EMM_MultiScaleSDGrid (void) | |
| create More... | |
| virtual | ~EMM_MultiScaleSDGrid (void) |
| destroy More... | |
| virtual void | initialize (const tDimension &dim, const tUInteger &Nx, const tUInteger &Ny, const tUInteger &Nz, const tBoolean &Px, const tBoolean &Py, const tBoolean &Pz, const tUInteger &l) |
| set the discretization More... | |
| void | setZonalLevelsNumber (const tUInteger &nLevels) |
| set the number of levels with are divied in zones More... | |
| tUCInt | getShiftZone (const tUCInt &z) const |
| compute the shift zone More... | |
| tBoolean | computeValuesOnShiftFineGrid (const tUIndex &nCells, const tDimension &dim, const tReal *M, const tUCInt &z, tReal *Mz) const |
| compute M on shift grid at zone z by periodicity More... | |
| void | meanValuesFromShiftFineGridToCoarseGrid (const tUIndex &nCells, const tDimension &dim, const tUCInt &z, const tReal *Mz, tReal *M) const |
| compute M at zone z of the coarse grid from the shift fine grid More... | |
| tBoolean | resetValuesWithinShiftZone (const tUIndex &nCells, const tDimension &dim, const tUCInt &z, tReal *Mz) const |
| tBoolean | addValuesFromGridToZoneFinestGrid (const tUInteger &twoPowerLp1, const tDimension &dim, const tUInteger &Nx, const tUInteger &Ny, const tUInteger &Nz, const tUCInt &z, tInteger &Sx, tInteger &Sy, tInteger &Sz, const tReal *Hz, tReal *H) const |
| add values from a large grid to the finest grid by zone More... | |
| tBoolean | addValuesFromShiftFineGridToFinestGrid (const tUIndex &nCells, const tDimension &dim, const tUInteger &twoPowerL, const tUCInt &z, const tReal *Hz, tReal *H) const |
| add the contribution of Hz from shift grid of zone z at level l to H on zone z at level 0 More... | |
| tBoolean | addValuesFromCoarseGridToFinestGrid (const tUIndex &nCells, const tDimension &dim, const tUInteger &twoPowerL, const tUCInt &z, const tReal *Hz, tReal *H) const |
| add the contribution of H at level l reset to 0 on zone z to H on finest grid at level 0 in zone z More... | |
| void | meanValuesFromFineToCoarseGrid (const tUIndex &nCells, const tDimension &dim, const tReal *Mf, tReal *Ml) const |
| compute the field in a corse field from its fine grid. More... | |
| void | completeValuesOutsideFineGridByPeriodicity (const tUIndex &nCells, const tDimension &dim, tReal *Ml) const |
| complete the values of the field in the coarse grid is set from its values in its included fine grid by periodicity More... | |
| tBoolean | resetValuesWithinCenteredZone (const tUIndex &nCells, const tDimension &dim, tReal *Mz) const |
| void | addValuesFromCoarseGridToFinestGrid (const tUIndex &nCells, const tDimension &dim, const tUInteger &twoPowerL, const tReal *Ml, tReal *Mf) const |
add the value of the field defined in coarse grid 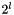 bigger than its finest grid into the field defined in its finest grid More... bigger than its finest grid into the field defined in its finest grid More... | |
| void | setToeplitzMatrix (SP::MATH_MultiLevelsToeplitzMatrix toeplitz) |
| setthe toeplitz associated matrix More... | |
| tUInteger | computeLevelsNumber (const tUInteger &Nx, const tUInteger &Ny, const tUInteger &Nz, const tBoolean &isXPeriodic, const tBoolean &isYPeriodic, const tBoolean &isZPeriodic) const |
| compute the optimal levels number More... | |
| const tUCInt & | getFineElementsNumberPerCoarseElement () const |
| get the number of elements of the fine grid per cell of the corse grid More... | |
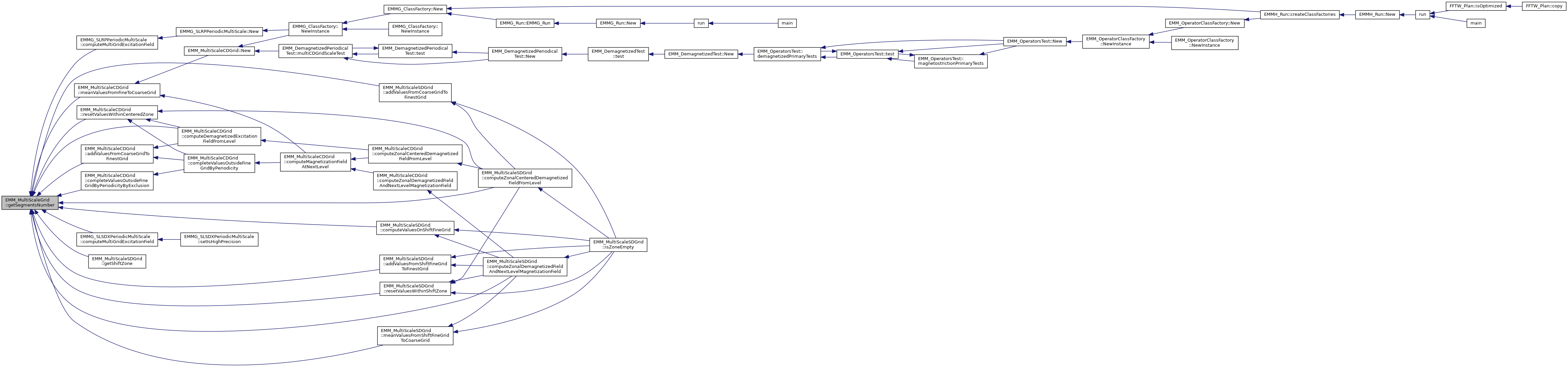
| void | getSegmentsNumber (tUInteger &Nx, tUInteger &Ny, tUInteger &Nz) const |
| get the segments number in all directions More... | |
| const tUInteger * | getSegmentsNumber () const |
| get the segments number per dierction More... | |
| const tBoolean * | getPeriodicDirections () const |
| get the periodicity per direction More... | |
| void | getPeriodicDirections (tBoolean &isXPeriodic, tBoolean &isYPeriodic, tBoolean &isZPeriodic) const |
| get the periodicity per direction More... | |
| const tUInteger & | getLevelsNumber () const |
| get the leves number More... | |
| const MATH_MultiLevelsToeplitzMatrix & | getToeplitzMatrix () const |
| get the toeplitz matrix More... | |
| EMM_RealField & | getLevelMagnetizationField () |
| get the magnetization field at level l More... | |
| EMM_RealField & | getLevelUpMagnetizationField () |
| get the magnetization field at level l+1 More... | |
| EMM_RealField & | getZonalMagnetizationField () |
| get the magnetization field at zone More... | |
| virtual void | computeMultiGridExcitationField (const tUIndex &nCells, const tDimension &dim, const tReal *sigmaM, tReal *H) |
| compute the magnetic excitation field by superposition of multi scale grids More... | |
| virtual tString | toString () const |
| return the class information in a tString More... | |
| void | getSharedPointer (SP::CORE_Object &p) |
| get the shared pointer of this class into p More... | |
| void | getSharedPointer (SPC::CORE_Object &p) const |
| get the shared pointer of this class into p More... | |
| tString | getClassName () const |
| return the class name of the object More... | |
| tString | getIdentityString () const |
| return the identity string of the object of the form className_at_address More... | |
| tString | getPointerAddress () const |
| return the identity string of the object More... | |
| template<class T > | |
| tBoolean | isInstanceOf () const |
| test if the clas T is an instance of this class More... | |
| tBoolean | isInstanceOf (const tString &name) const |
| test if the object is an instance of className More... | |
Static Public Member Functions | |
| static SP::EMM_MultiScaleSDGrid | New () |
| build a new instance of class More... | |
| static tUCInt | getShiftZone (const tUInteger &Nx, const tUInteger &Ny, const tUInteger &Nz, const tUCInt &z) |
| compute the shift zone More... | |
| static tBoolean | isZoneEmpty (const tUInteger &Nx, const tUInteger &Ny, const tUInteger &Nz, const tUCInt &z) |
| return true if the zone is empty More... | |
| static tBoolean | isZoneEmpty (const tUInteger N[], const tUCInt &z) |
| return true if the zone is empty More... | |
| static tBoolean | resetBlockValues (const tDimension &dim, const tUInteger &Nx, const tUInteger &Ny, const tUInteger &Nz, const tUInteger &iMin, const tUInteger &iMax, const tUInteger &jMin, const tUInteger &jMax, const tUInteger &kMin, const tUInteger &kMax, tReal *M) |
| reset the values in a block grid [iMin,iMax[x[jMin,jMax[x[kMin,kMax[ of dimension dim per point inside a grid of size [0,Nx[x[0,Ny[x[0,Nz[ More... | |
| static void | setIsMemoryChecked (const tBoolean &v) |
| set if the memory checking is used More... | |
| static void | setOut (SP::CORE_Out out) |
| set the output stream More... | |
| static void | resetOut () |
| reset the output stream More... | |
| static void | setThread (SP::CORE_Thread thread) |
| set the thread More... | |
| static void | resetThread () |
| reset the output stream More... | |
| static CORE_Out & | out () |
| get the output More... | |
| static SP::CORE_Out | getOut () |
| get the output More... | |
| static CORE_Thread & | getThread () |
| get the profilier More... | |
| static const tBoolean & | isMemoryChecked () |
| get if the memory checking is used More... | |
| static tString | getClassName (const tString &identityString) |
| return the class name of the object More... | |
| template<class T > | |
| static tString | getTypeName () |
| get type name More... | |
| static tBoolean | is64Architecture () |
| return true if the machine is a 64 bits machine More... | |
| static tBoolean | is32Architecture () |
| return true if the machine is a 32 bits machine More... | |
| static tString | pointer2String (const void *obj) |
| return the string representation of a pointer More... | |
| static void | printObjectsInMemory (ostream &f) |
| print object in memory More... | |
| static void | printObjectsInMemory () |
| print object in memory in the standart output More... | |
| static tChar | getMaxChar () |
| get the max value for tChar type More... | |
| static tChar | getMinChar () |
| get the min value for tChar type More... | |
| static tUChar | getMaxUChar () |
| get the max value for tUChar type More... | |
| static tUChar | getMinUChar () |
| get the min value for tUChar type More... | |
| static tSInt | getMaxSInt () |
| get the max value for tSInt type More... | |
| static tSInt | getMinSInt () |
| get the min value for tSInt type More... | |
| static tUSInt | getMaxUSInt () |
| get the max value for tUSInt type More... | |
| static tUSInt | getMinUSInt () |
| get the min value for tUSInt type More... | |
| static tInt | getMaxInt () |
| get the max value for tInt type More... | |
| static tInt | getMinInt () |
| get the min value for tInt type More... | |
| static tUInt | getMaxUInt () |
| get the max value for tUInt type More... | |
| static tUInt | getMinUInt () |
| get the min value for tUInt type More... | |
| static tLInt | getMaxLInt () |
| get the max value for tLInt type More... | |
| static tLInt | getMinLInt () |
| get the min value for tLInt type More... | |
| static tULInt | getMaxULInt () |
| get the max value for tULInt type More... | |
| static tULInt | getMinULInt () |
| get the min value for tULInt type More... | |
| static tLLInt | getMaxLLInt () |
| get the max value for tULInt type More... | |
| static tLLInt | getMinLLInt () |
| get the min value for tLLInt type More... | |
| static tULLInt | getMaxULLInt () |
| get the max value for tULLInt type More... | |
| static tULLInt | getMinULLInt () |
| get the min value for tULLInt type More... | |
| static tFloat | getMaxFloat () |
| get the max value for tFloat type More... | |
| static tFloat | getMinFloat () |
| get the min value for tFloat type More... | |
| template<class T > | |
| static T | getEpsilon () |
| get the epsilon value for T type More... | |
| template<class T > | |
| static T | getInfinity () |
| get the infinity for T type More... | |
| static tFloat | getFloatEpsilon () |
| get the epsilon value for tFloat type More... | |
| static tFloat | getFloatInfinity () |
| get the infinity value for tFloat type More... | |
| static tDouble | getMaxDouble () |
| get the max value for tDouble type More... | |
| static tDouble | getMinDouble () |
| get the min value for tDouble type More... | |
| static tDouble | getDoubleInfinity () |
| get the infinity value for tFloat type More... | |
| static tDouble | getDoubleEpsilon () |
| get the epsilon value for tDouble type More... | |
| static tLDouble | getMinLDouble () |
| get the min value for tLDouble type More... | |
| static tLDouble | getMaxLDouble () |
| get the max value for tLDouble type More... | |
| static tLDouble | getLDoubleEpsilon () |
| get the epsilon value for tLDouble type More... | |
| static tDouble | getLDoubleInfinity () |
| get the infinity value for tDouble type More... | |
| static tIndex | getMaxIndex () |
| get the max value for the array/vector indexing type More... | |
| static tIndex | getMinIndex () |
| get the min value for the array/vector indexing type More... | |
| static tUIndex | getMaxUIndex () |
| get the max value for difference the array/vector indexing type More... | |
| static tUIndex | getMinUIndex () |
| get the min value for difference the array/vector indexing type More... | |
| static tFlag | getMaxFlag () |
| get the max value for the tFlag type More... | |
| static tFlag | getMinFlag () |
| get the min value for the tFlag type More... | |
| static tUInteger | getMaxUInteger () |
| get the max value for the unsigned integer type More... | |
| static tUInteger | getMinUInteger () |
| get the min value for the unsigned integer type More... | |
| static tInteger | getMaxInteger () |
| get the max value for the integer type More... | |
| static tInteger | getMinInteger () |
| get the min value for the integer type More... | |
| static tReal | getMaxReal () |
| get the max value for the real type More... | |
| static tReal | getMinReal () |
| get the min value for the real type More... | |
| static tReal | getRealEpsilon () |
| get the eps which is the difference between 1 and the least value greater than 1 that is representable. More... | |
| static tReal | getRealInfinity () |
| get the infinity value More... | |
| template<class T > | |
| static T | computeEpsilon () |
| compute epsilon More... | |
Static Public Attributes | |
| static tBoolean | SAVE_H_M_AT_LEVEL_1 =false |
| static const tReal | Mu0 =4*M_PI*1e-07 |
| static const tReal | Gamma =-1.7e11 |
| static const tDimension | X =0 |
| static const tDimension | Y =1 |
| static const tDimension | Z =2 |
| static const tReal | NULL_VALUE [] ={0,0,0} |
Protected Member Functions | |
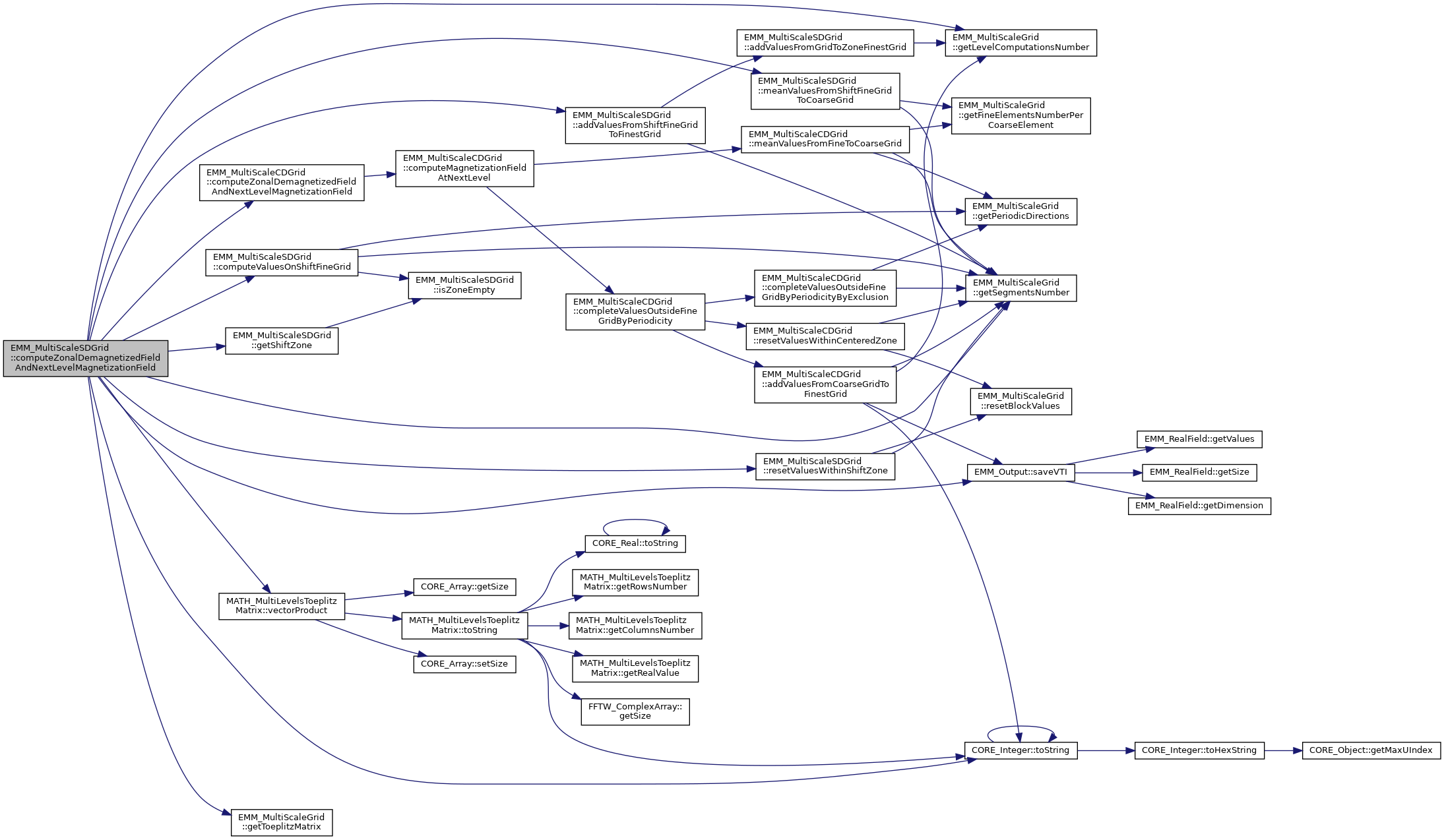
| virtual void | computeZonalDemagnetizedFieldAndNextLevelMagnetizationField (const tUInteger &twoPowerL, const tUIndex &nCells, const tDimension &dim, const tReal *Ml, tReal *Mz, tReal *Mlp1, tReal *H0) const |
| compute the zonal demagnetized field added to demagnetized field at level 0 and compute the magnetization field at level l+1 More... | |
| virtual void | computeZonalCenteredDemagnetizedFieldFromLevel (const tUInteger &twoPowerL, const tUIndex &nCells, const tDimension &dim, tReal *Ml, tReal *Mz, tReal *H0) const |
| compute the centered demagnetized field of level l outside zone anad add it to demagnetized field at level 0 More... | |
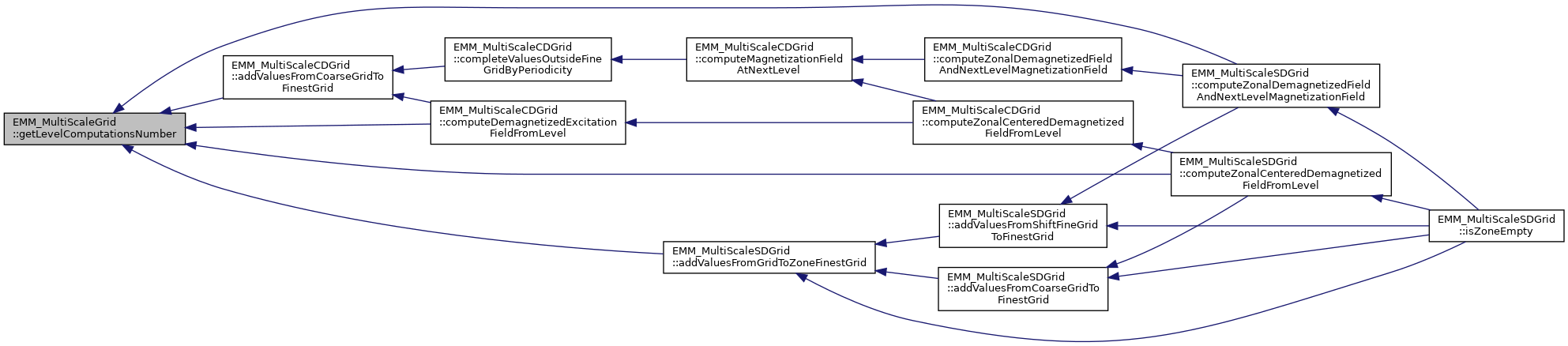
| tUInteger & | getLevelComputationsNumber () |
| return the number of calls of the level computations only for debug More... | |
| const tUInteger & | getLevelComputationsNumber () const |
| return the number of calls of the level computations only for debug More... | |
| virtual void | toDoAfterThisSetting () |
| method called after the setting of the shared pointer this method can only be called once. More... | |
| void | setThis (SP::CORE_Object p) |
| set this weak shared pointer called toDoAfterThis setting method More... | |
Private Member Functions | |
| SP_OBJECT (EMM_MultiScaleSDGrid) | |
Private Attributes | |
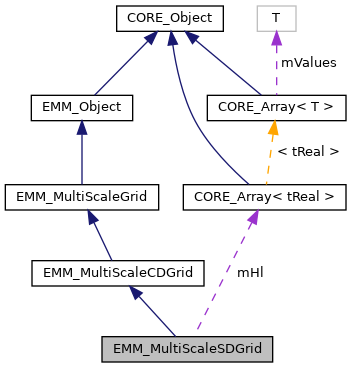
| tUInteger | mTwoPowerZonalLevelsNumber |
| SP::CORE_RealArray | mHl |
Detailed Description
This class describes the building of fields on multiscale shift dioptic grids initialized by the initialize() method.
For building centered dyotic coarse grids, the number of segments in each direction must be 1 or a pair number.
For computing the magnetic excitation field for periodic domain, a sequence of l-dyotic grids is built: the grid of level l is included into the grid of level l+1. The grid of level l+1 is twice the size of the grid at level l in each direction. The total magnetic excitation field is built by superposition of the magnetic excitation at each level.
To improve the accuracy of the CDG method see EMM_MultiScaleCDGrid class, we compute the magnetic excitation on different zones of the domain: the finest grid are shift over the coarse grid to compute the magnetic excitation field on cells with same size either on the coarse or on the fine grid.
The method is as follow:
- 1. suppose the magnetization
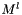 at level l is computed with
at level l is computed with 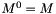 over the domain
over the domain 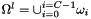 . We suppose that
. We suppose that 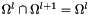
- 2. for each recovering zone
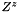 of the coarse grid
of the coarse grid 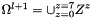 , it computes the magnetization field
, it computes the magnetization field 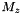 on the fine grid shifted to the zone z
on the fine grid shifted to the zone z 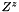 within the coarse grid see computeValuesOnShiftFineGrid() :
within the coarse grid see computeValuesOnShiftFineGrid() :- 2.a
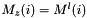 for all cell
for all cell 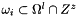 inside the fine grid at level l and inside the shift fine grid over the coarse grid at level l+1.
inside the fine grid at level l and inside the shift fine grid over the coarse grid at level l+1. - 2.b
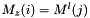 for all cell
for all cell 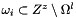 outside the fine grid at level l and inside the shift fine grid over the coarse grid at level l+1,
outside the fine grid at level l and inside the shift fine grid over the coarse grid at level l+1, 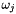 is the periodic cell corresponding to cell
is the periodic cell corresponding to cell 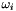 from the fine grid at level l
from the fine grid at level l - 2.c builds the magnetization field
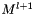 on the coarse grid at level l+1 over the zone z by using the mean of
on the coarse grid at level l+1 over the zone z by using the mean of 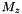 . see meanValuesFromFineToCoarseGrid() :
. see meanValuesFromFineToCoarseGrid() : 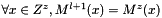
- 2.d
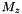 is set to 0 on all cell
is set to 0 on all cell 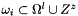 inside the fine grid at level l and inside the shift fine grid over the coarse grid at level l+1; see resetValuesWithinCenteredZone()
inside the fine grid at level l and inside the shift fine grid over the coarse grid at level l+1; see resetValuesWithinCenteredZone() - 2.e
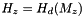
- 2.f adds the demagnetized field
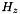 on the common cells
on the common cells 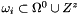 within the zone z in the grid at level l+1 and on the grid at level 0
within the zone z in the grid at level l+1 and on the grid at level 0 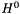 see addValuesFromShiftFineGridToFinestGrid()
see addValuesFromShiftFineGridToFinestGrid()
- 2.a
The step 2 computes only the contribution of the magnetization field on the zone Z at the coarse grid at level l+1 to the demagnetized field at level 0 on zone Z. The cells outside the zone z of the coarse grid at level l+1 have also an influence on the demagnetized field on the zone Z at level 0. The step 5 will take into account this influence:
- 3. step 2.c computes the field
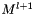 on the coarse grid at level l+1
on the coarse grid at level l+1 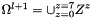 .
. - 4. reset the influence of the fine grid :
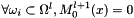 and
and 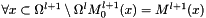 see resetValuesWithinCenteredZone()
see resetValuesWithinCenteredZone() - 5. for all zone Z,
- 5.a
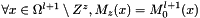 and
and 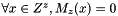 builds the magnetization field outside the zone Z of the coarse grid. see resetValuesWithinShiftZone()
builds the magnetization field outside the zone Z of the coarse grid. see resetValuesWithinShiftZone() - 5.b computes
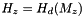
- 5.c adds the demagnetized field
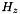 on the common cells
on the common cells 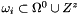 within the zone z in the grid at level l+1 and on the grid at level 0
within the zone z in the grid at level l+1 and on the grid at level 0 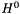 see addValuesFromCoarseGridToFinestGrid().
see addValuesFromCoarseGridToFinestGrid().
- 5.a
- 6. goes to step 1 to compute the contribution of the next level with
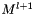 built at step 2.c
built at step 2.c
The algorithm of the step 2 can be illustrated as follow :
The algorithm of the step 5 can be illustrated as follow :
@author Stephane Despreaux @version 1.0
Constructor & Destructor Documentation
◆ EMM_MultiScaleSDGrid()
| EMM_MultiScaleSDGrid::EMM_MultiScaleSDGrid | ( | void | ) |
create
References mHl, mTwoPowerZonalLevelsNumber, and CORE_Array< tReal >::New().
Referenced by New().


◆ ~EMM_MultiScaleSDGrid()
|
virtual |
destroy
Member Function Documentation
◆ addValuesFromCoarseGridToFinestGrid() [1/2]
|
inherited |
add the value of the field defined in coarse grid 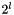 bigger than its finest grid into the field defined in its finest grid
bigger than its finest grid into the field defined in its finest grid
- Parameters
-
[in] nCells number of elements of the field [in] dim dimension of the field [in] twoPowerL : step size of the coarse grid with respect of the finest grid [in] Ml : the large field values of size dim . Nx . Ny . Nz [in,out] Mf : the fine field values of size dim . Nx . Ny . Nz
add the value of the field Ml to the value of the field Mf on the cells in common.
For each cell of the finest grid, the corresponding cell of the coarse grid is computed and the values of the field at the coarse element is added to the value of the field at the fine element.
The corresponding coarse elements to the element from the fine grid is computed such that the coarse element contains the center of the element of the fine grid by the following relation.
For each element (i,j,k) of the grid at level 0, the corresponding element (I(i),J(j),K(k)) of the grid at level l is searched such that the center of the element (i,j,k) of the grid at level 0 is inside the element (I,J,K) of the grid at level l.
The left boundary of the grid at level l is 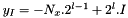 when the origin is at the center of the grid
when the origin is at the center of the grid
The center of the grid at level 0 is 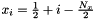 when the origin is at the center of the grid
when the origin is at the center of the grid
So, to search the cell of the grid at level l containing the center of the grid at level 0 leads to 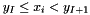 . We conclude that
. We conclude that
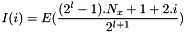
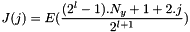
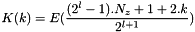 .
.
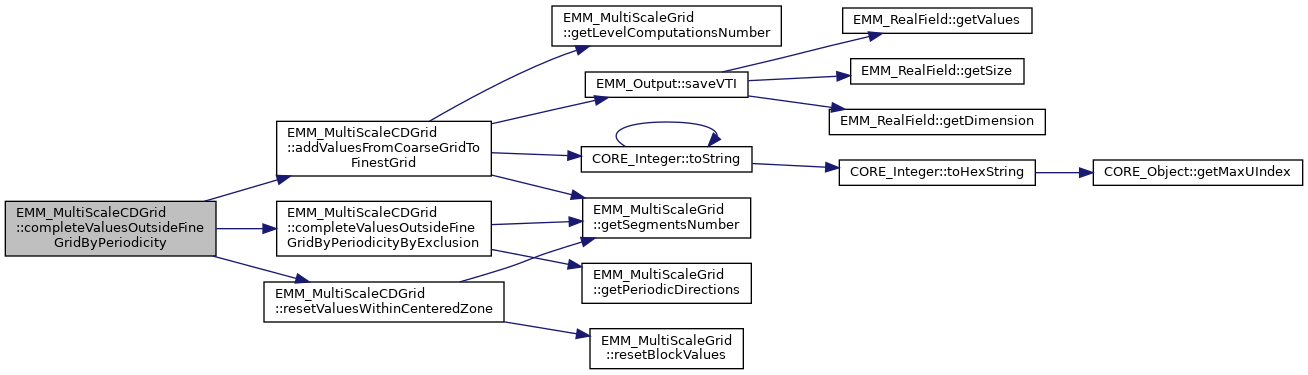
References EMM_MultiScaleGrid::getLevelComputationsNumber(), EMM_MultiScaleGrid::getSegmentsNumber(), null, OMP_GET_THREAD_ID, OMP_GET_THREADS_NUMBER, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, EMM_Output::saveVTI(), tDimension, CORE_Integer::toString(), tReal, tUIndex, and tUInteger.
Referenced by EMM_MultiScaleCDGrid::completeValuesOutsideFineGridByPeriodicity(), and EMM_MultiScaleCDGrid::computeDemagnetizedExcitationFieldFromLevel().
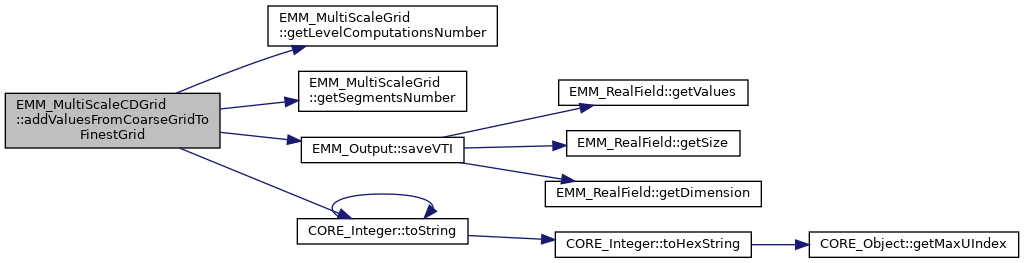

◆ addValuesFromCoarseGridToFinestGrid() [2/2]
| tBoolean EMM_MultiScaleSDGrid::addValuesFromCoarseGridToFinestGrid | ( | const tUIndex & | nCells, |
| const tDimension & | dim, | ||
| const tUInteger & | twoPowerL, | ||
| const tUCInt & | z, | ||
| const tReal * | Hz, | ||
| tReal * | H | ||
| ) | const |
add the contribution of H at level l reset to 0 on zone z to H on finest grid at level 0 in zone z
- Parameters
-
[in] nCells : number of cells of the mesh [in] dim dimension of each point of the mesh [in] twoPowerL ratio 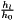 where
where 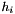 is the step size at level l
is the step size at level l [in] z zone of the finest grid to add the values [in] Hz demagnetized field values of size nCells x dim of the coarse grid at level l, reset to 0 on zone z [in,out] H magnetic excitation values of size nCells x dim of the grid at level 0
- Returns
- false if the grid is empty
The algorithm consists in finding the segment of the coarse grid at level l and zone z 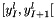 such that it contains the center of the cell p at the finest grid at level 0 :
such that it contains the center of the cell p at the finest grid at level 0 :
![$ x_p = [-Nx/2+p+1/2].h $](form_511.png) where h is the step size of the finest grid with p in [0,Nx/2[ for zone 0 or [Nx/2,Nx[ for zone 1
where h is the step size of the finest grid with p in [0,Nx/2[ for zone 0 or [Nx/2,Nx[ for zone 1
The bounds of the cell of the coarse grid at level l with step size 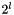 is
is ![$ y^l_I=[- N_x . 2^{l-1} + 2^{l} i ] h $](form_519.png)
so that we have 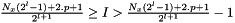 , so that :
, so that :
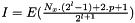
References addValuesFromGridToZoneFinestGrid(), EMM_MultiScaleGrid::getSegmentsNumber(), tInteger, and tUInteger.
Referenced by computeZonalCenteredDemagnetizedFieldFromLevel(), and isZoneEmpty().


◆ addValuesFromGridToZoneFinestGrid()
| tBoolean EMM_MultiScaleSDGrid::addValuesFromGridToZoneFinestGrid | ( | const tUInteger & | twoPowerLp1, |
| const tDimension & | dim, | ||
| const tUInteger & | Nx, | ||
| const tUInteger & | Ny, | ||
| const tUInteger & | Nz, | ||
| const tUCInt & | z, | ||
| tInteger & | Sx, | ||
| tInteger & | Sy, | ||
| tInteger & | Sz, | ||
| const tReal * | Hz, | ||
| tReal * | H | ||
| ) | const |
add values from a large grid to the finest grid by zone
- Parameters
-
[in] twoPowerLp1 : twice the size of the large grid [in] dim : dimension of each point of the grid [in] Nx : number of segments in the x-direction [in] Ny : number of segments in the y-direction [in] Nz : number of segments in the z-direction [in] z : index of the zone [in,out] Sx : grid translator on x-coordinate [in,out] Sy : grid translator on y-coordinate [in,out] Sz : grid translator on z-coordinate [in] Hz : demagnetized field on large grid in zone [in] H : demagnetized field on finest grid
- Returns
- false if the zone is empty
Note 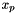 is the center of the cell of the finest grid
is the center of the cell of the finest grid 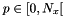
we have 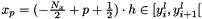 where
where
- h is the step size of the finest grid
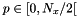 for zone 0 and
for zone 0 and 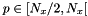 for zone 1.
for zone 1.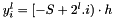
So we have 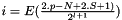
and S:=2S-N+1.
we build : H[i]+=Hz[p]
References EMM_MultiScaleGrid::getLevelComputationsNumber(), mHl, OMP_GET_THREAD_ID, OMP_GET_THREADS_NUMBER, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tDimension, tReal, tUCInt, tUIndex, and tUInteger.
Referenced by addValuesFromCoarseGridToFinestGrid(), addValuesFromShiftFineGridToFinestGrid(), and isZoneEmpty().

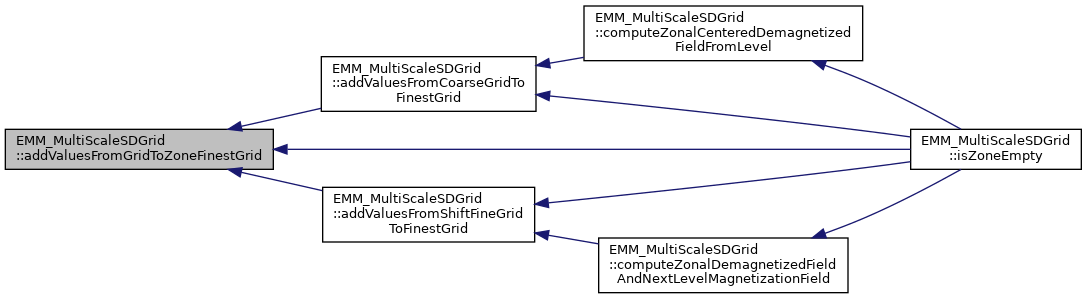
◆ addValuesFromShiftFineGridToFinestGrid()
| tBoolean EMM_MultiScaleSDGrid::addValuesFromShiftFineGridToFinestGrid | ( | const tUIndex & | nCells, |
| const tDimension & | dim, | ||
| const tUInteger & | twoPowerL, | ||
| const tUCInt & | z, | ||
| const tReal * | Hz, | ||
| tReal * | H | ||
| ) | const |
add the contribution of Hz from shift grid of zone z at level l to H on zone z at level 0
- Parameters
-
[in] nCells : number of cells of the mesh [in] dim dimension of each point of the mesh [in] twoPowerL : ratio 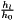 where
where 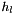 is the step sizes at level l
is the step sizes at level l [in] z zone of the finest grid to add the values [in] Hz magnetic excitation values of size nCells x dim at zone z of the grid at level l [in,out] H magnetic excitation values of size nCells x dim of the grid at level 0
- Returns
- false if the grid is empty
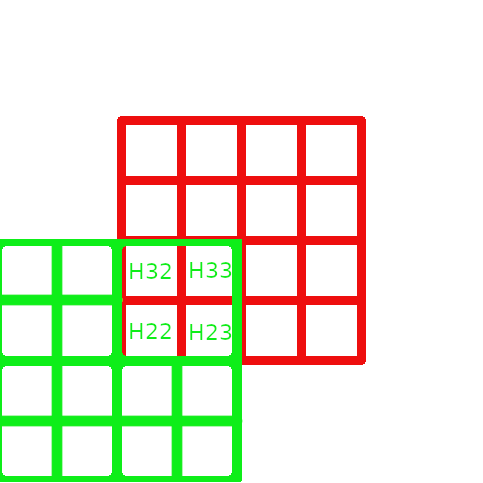 |
only the contribution of Hz on the cells in common with shift fine grid at level l+1 and with the grid at level 0 is added to magnetic excitation field for M at level 0 |
The algorithm consists in finding the segment of the shift fine grid at level l and zone z 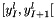 such that it contains the center of the cell p at the finest grid at level 0 :
such that it contains the center of the cell p at the finest grid at level 0 :
![$ x_p = [-Nx/2+p+1/2].h $](form_511.png) where h is the step size with p in [0,Nx/2[ for zone 0 or [Nx/2,Nx[ for zone 1
where h is the step size with p in [0,Nx/2[ for zone 0 or [Nx/2,Nx[ for zone 1
The bounds of the cell of the shift fine grid at zone z and at level l (step size is 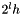 ) is is
) is is
![$ y^l_I=[- N_x . 2^{l} + 2^{l} i ] h $](form_513.png) for zone 0
for zone 0![$ y^l_I=[ 2^{l} i ] h $](form_514.png) for zone 1
for zone 1![$ y^l_I=[- N_x . 2^{l}.1_{z=0} + 2^{l} i ] h $](form_515.png) for zone z
for zone z
so that we have 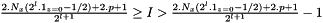 , so that :
, so that :
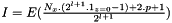
References addValuesFromGridToZoneFinestGrid(), EMM_MultiScaleGrid::getSegmentsNumber(), tInteger, tUCInt, and tUInteger.
Referenced by computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), and isZoneEmpty().


◆ completeValuesOutsideFineGridByPeriodicity()
|
inlineinherited |
complete the values of the field in the coarse grid is set from its values in its included fine grid by periodicity
- Parameters
-
[in] nCells number of elements of the mesh [in] dim dimension of the field [in,out] Ml : the coarse field values of size dim . nCells
| Step 1 |  |
M at level l |
| Step 2 | 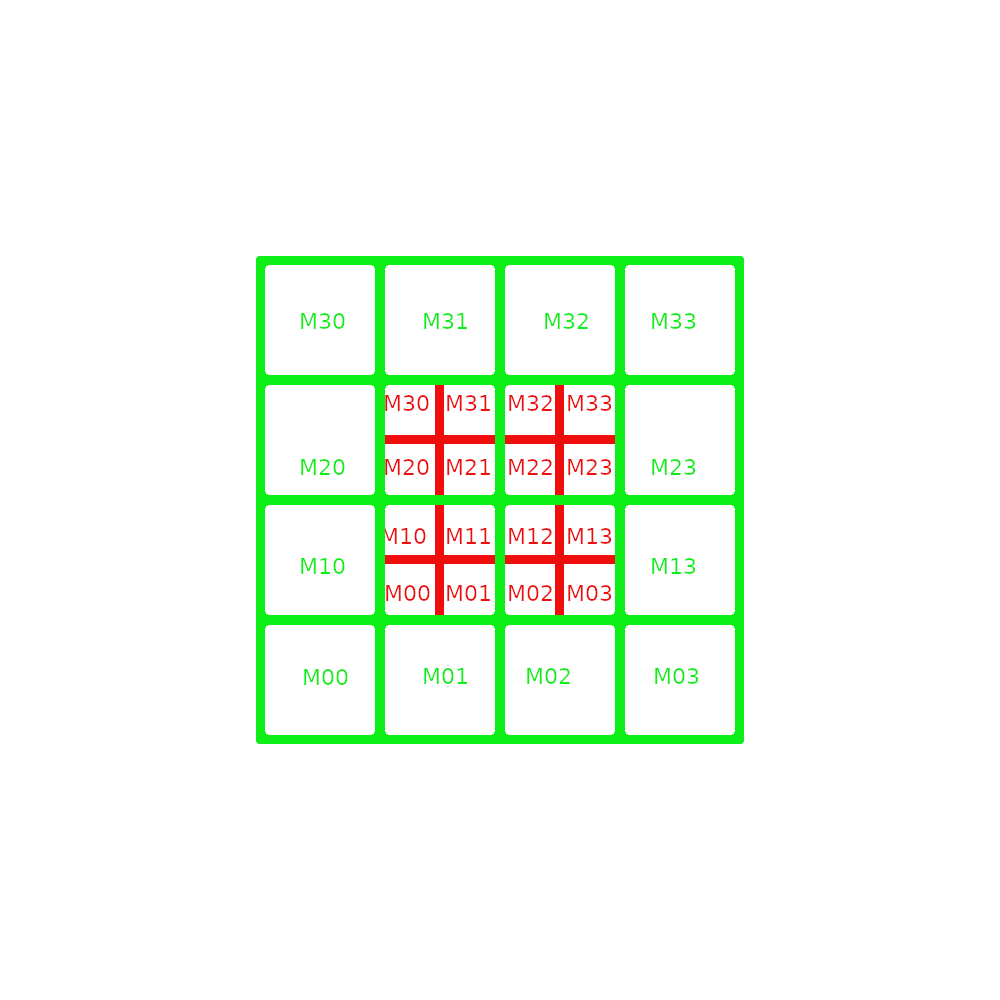 |
M at level l+1 |
If there is periodicity on x, we have:
If there is periodicity on y, we have:
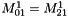
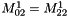
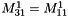
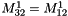
If there is periodicity on x and y, we have in addition:
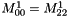
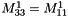
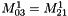
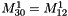
References EMM_MultiScaleCDGrid::addValuesFromCoarseGridToFinestGrid(), EMM_MultiScaleCDGrid::completeValuesOutsideFineGridByPeriodicityByExclusion(), EMM_MultiScaleCDGrid::resetValuesWithinCenteredZone(), tBoolean, tDimension, tReal, tUIndex, and tUInteger.
Referenced by EMM_MultiScaleCDGrid::computeMagnetizationFieldAtNextLevel().

◆ computeEpsilon()
|
inlinestaticinherited |
compute epsilon
- Returns
- the epsilon value eps=10^{-p/3} where p is defined by getEpsilon()=10^{-p}
◆ computeLevelsNumber()
|
inherited |
compute the optimal levels number
- Parameters
-
Nx number of segments along x-direction Ny number of segments along y-direction Nz number of segments along z-direction isXPeriodic true if the x-direction is periodic isYPeriodic true if the y-direction is periodic isZPeriodic true if the z-direction is periodic
The level number per direction 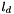 is such that if
is such that if 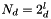 If the domain is not periodic the level number is 0
If the domain is not periodic the level number is 0
- Returns
- the minimum of the level number for all directions
References CORE_Object::getMaxUInteger(), tBoolean, tUInteger, and tUSInt.
Referenced by EMM_MultiScaleGrid::setToeplitzMatrix().


◆ computeMultiGridExcitationField()
|
virtualinherited |
compute the magnetic excitation field by superposition of multi scale grids
- Parameters
-
[in] nCells : number of cells of the mesh [in] dim dimension of each point of the mesh [in] sigmaM magnetization values of size nCells x dim not necessarly normalized : sigmaM=sigma.M [out] H return excitation magnetic values of size nCells x dim
The following algorithm needs 3 temporary fields 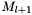 ,
, 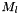 and
and 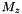 for computing by zone
for computing by zone
Computes the magnetic excitation field as follow:
- l=0
- computes H corresponding to sigma.M
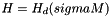 see MATH_ToeplitzMatrix::vectorProduct()
see MATH_ToeplitzMatrix::vectorProduct() - l=1, computeZonalDemagnetizedFieldAndNextLevelMagnetizationField() :
- add the contribution of the demagnetized field within shift zonal grids from level 0 into the demagnetized field at level 0
- builds M for level 1 by interpolation of M at level 0
- for all l in [1,L[
- computeZonalDemagnetizedFieldAndNextLevelMagnetizationField() :
- add the contribution of the demagnetized field within shift zonal grids from level l into the demagnetized field at level 0
- builds M for level l+1 by interpolation of M at level l
- computeZonalCenteredDemagnetizedFieldFromLevel()
- add the contribution of the demagnetized fiel at level l within centered coarse grid exculed shift zonal grid z into the demagnetized field at level 0 in zone z
- next level :
- swaps
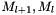
- l:=l+1
- swaps
- computeZonalDemagnetizedFieldAndNextLevelMagnetizationField() :
- compute H for last level l=L by the method computeZonalCenteredDemagnetizedFieldFromLevel()
- add the contribution of the demagnetized fiel at level l within centered coarse grid exculed shift zonal grid z into the demagnetized field at level 0 in zone z
Reimplemented in EMMG_SLSDXPeriodicMultiScale, and EMMG_SLRPPeriodicMultiScale.
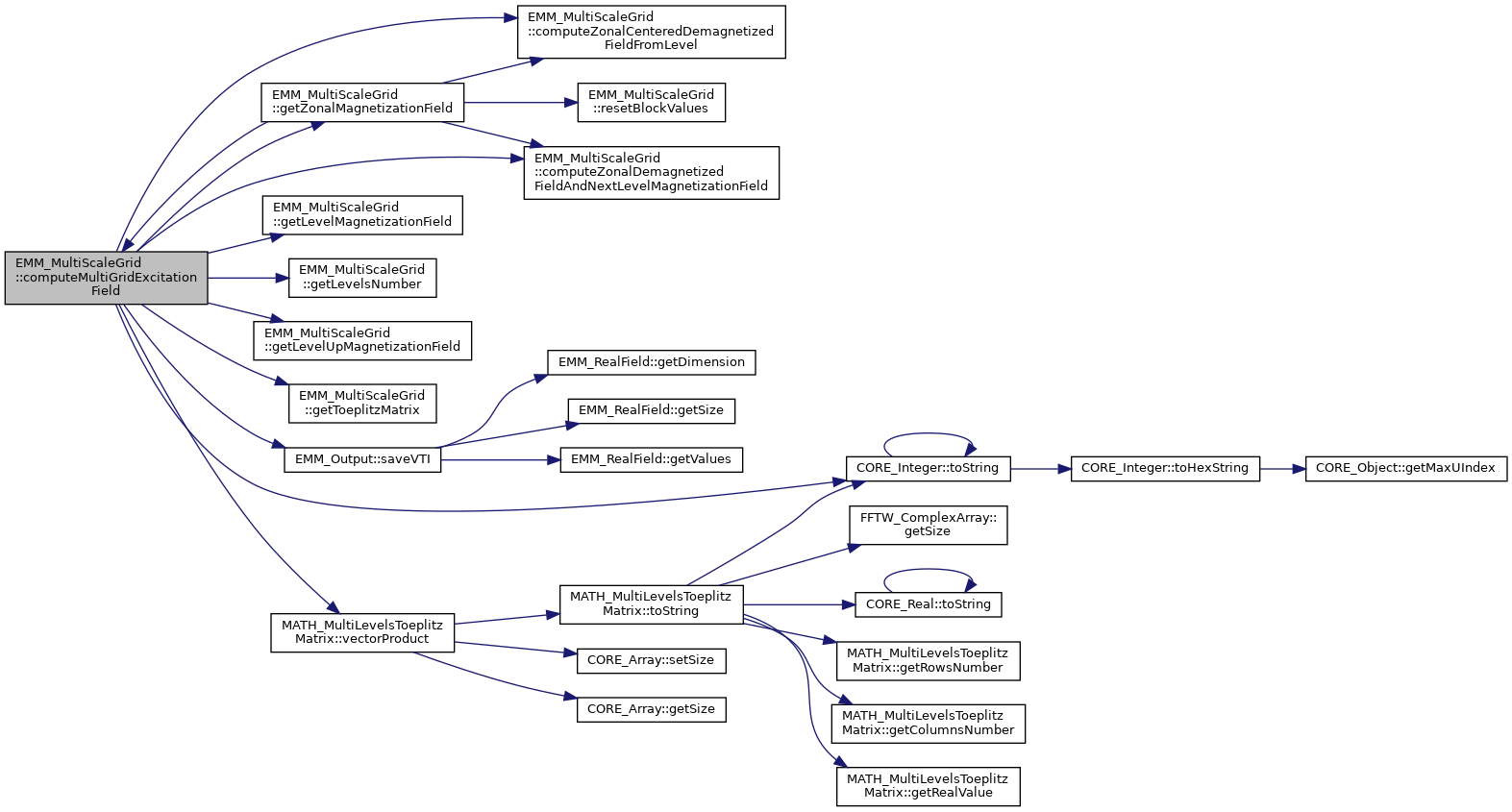
References EMM_MultiScaleGrid::computeZonalCenteredDemagnetizedFieldFromLevel(), EMM_MultiScaleGrid::computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), EMM_MultiScaleGrid::getLevelMagnetizationField(), EMM_MultiScaleGrid::getLevelsNumber(), EMM_MultiScaleGrid::getLevelUpMagnetizationField(), EMM_MultiScaleGrid::getToeplitzMatrix(), EMM_MultiScaleGrid::getZonalMagnetizationField(), EMM_MultiScaleGrid::mLevelComputationsNumber, EMM_MultiScaleGrid::mN, null, EMM_MultiScaleGrid::SAVE_H_M_AT_LEVEL_1, EMM_Output::saveVTI(), CORE_Integer::toString(), tReal, tUIndex, tUInteger, and MATH_MultiLevelsToeplitzMatrix::vectorProduct().
Referenced by EMM_MultiScaleGrid::getZonalMagnetizationField().

◆ computeValuesOnShiftFineGrid()
| tBoolean EMM_MultiScaleSDGrid::computeValuesOnShiftFineGrid | ( | const tUIndex & | nCells, |
| const tDimension & | dim, | ||
| const tReal * | M, | ||
| const tUCInt & | z, | ||
| tReal * | Mz | ||
| ) | const |
compute M on shift grid at zone z by periodicity
- Parameters
-
[in] nCells : number of cells of the mesh [in] dim dimension of each point of the mesh [in] M magnetization values of size nCells x dim on grid at level l [in] z zone of the grid at level l [out] Mz : magnetization values of size nCells x dim on shift grid at zone z of grid at level l
- Returns
- false if the volume of the zone z is null
Builds Mz on shift grid at zone z by copping values and by periodicity of M within the centered grid.
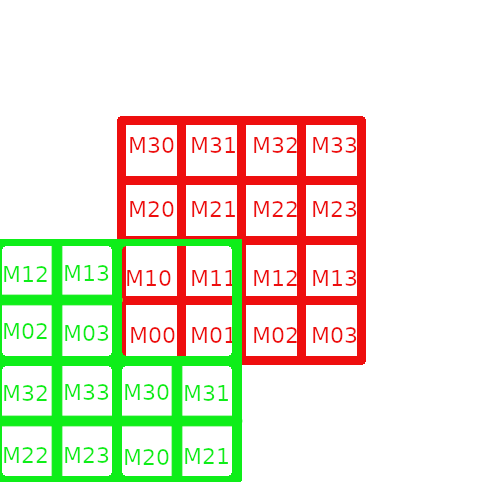 |
Mz at zone z built by copy and by periodicity from M at level l |
The algorithm is has follow:
- the centered grid indices varies within
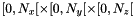
- computes the bounds of the shift grid at zone z:
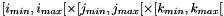 . for zone 0 the index of the shift grid is [-Nx/2,Nx/2[ or [Nx/2,Nx[ for zone 1
. for zone 0 the index of the shift grid is [-Nx/2,Nx/2[ or [Nx/2,Nx[ for zone 1 - if the zone is empty, return false.
- for all cells p inside the shift grid
- if the cell p is inside the centered grid,
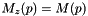
- if the cell p is outside the centered grid, computes the corresponding periodical cell q within the centered grid and
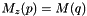 ; If the periodical cell q does not exists,
; If the periodical cell q does not exists, 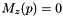
- if the cell p is inside the centered grid,
References EMM_MultiScaleGrid::getPeriodicDirections(), EMM_MultiScaleGrid::getSegmentsNumber(), isZoneEmpty(), null, OMP_GET_THREAD_ID, OMP_GET_THREADS_NUMBER, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tBoolean, tDimension, tInteger, tReal, tUCInt, tUIndex, and tUInteger.
Referenced by computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), and isZoneEmpty().
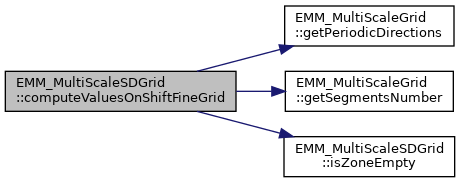

◆ computeZonalCenteredDemagnetizedFieldFromLevel()
|
protectedvirtual |
compute the centered demagnetized field of level l outside zone anad add it to demagnetized field at level 0
- Parameters
-
[in] twoPowerL : ratio size of the grid at level l [in] nCells : number of cells of the mesh [in] dim dimension of each point of the mesh [in,out] Ml magnetization values of size nCells x dim at level l [out] Mz magnetization at zone . Working field [in,out] H0 : demagnetized excitation field at level 0
Reimplemented from EMM_MultiScaleCDGrid.
References addValuesFromCoarseGridToFinestGrid(), EMM_MultiScaleCDGrid::computeZonalCenteredDemagnetizedFieldFromLevel(), EMM_MultiScaleGrid::getLevelComputationsNumber(), EMM_MultiScaleGrid::getSegmentsNumber(), EMM_MultiScaleGrid::getToeplitzMatrix(), isZoneEmpty(), mHl, mTwoPowerZonalLevelsNumber, EMM_MultiScaleCDGrid::resetValuesWithinCenteredZone(), resetValuesWithinShiftZone(), EMM_Output::saveVTI(), CORE_Integer::toString(), tReal, tUCInt, tUInteger, and MATH_MultiLevelsToeplitzMatrix::vectorProduct().
Referenced by isZoneEmpty().
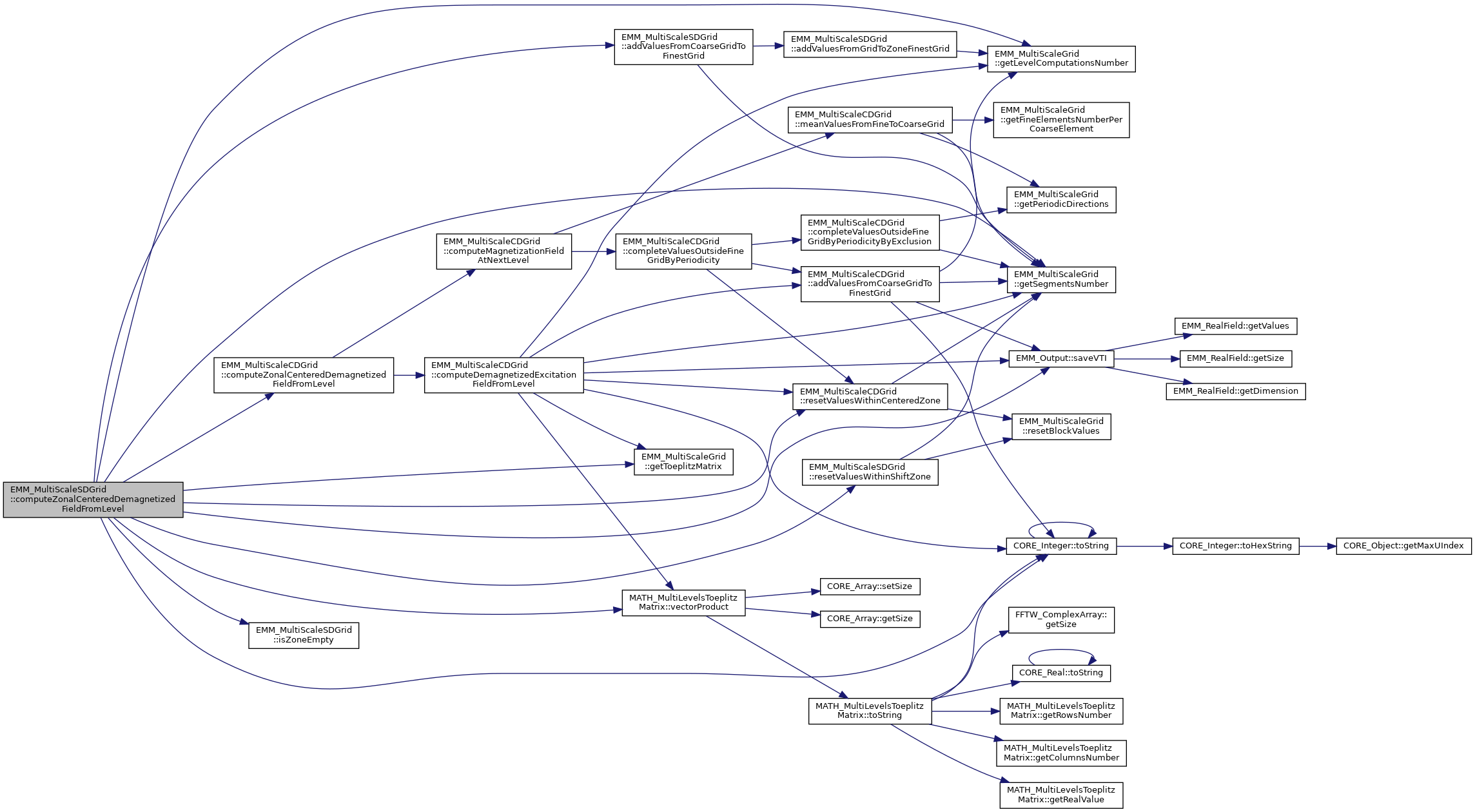

◆ computeZonalDemagnetizedFieldAndNextLevelMagnetizationField()
|
protectedvirtual |
compute the zonal demagnetized field added to demagnetized field at level 0 and compute the magnetization field at level l+1
- Parameters
-
[in] twoPowerL : ratio size of the grid at level l [in] nCells : number of cells of the mesh [in] dim dimension of each point of the mesh [in] Ml magnetization at level l [out] Mz magnetization at zone . Working field [in,out] Mlp1 magnetization values of size nCells x dim at level l+1 [in,out] H0 : demagnetized excitation field at level 0
Reimplemented from EMM_MultiScaleCDGrid.
References addValuesFromShiftFineGridToFinestGrid(), computeValuesOnShiftFineGrid(), EMM_MultiScaleCDGrid::computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), EMM_MultiScaleGrid::getLevelComputationsNumber(), EMM_MultiScaleGrid::getSegmentsNumber(), getShiftZone(), EMM_MultiScaleGrid::getToeplitzMatrix(), meanValuesFromShiftFineGridToCoarseGrid(), mHl, mTwoPowerZonalLevelsNumber, resetValuesWithinShiftZone(), EMM_Output::saveVTI(), tInteger, CORE_Integer::toString(), tReal, tUCInt, tUInteger, and MATH_MultiLevelsToeplitzMatrix::vectorProduct().
Referenced by isZoneEmpty().

◆ getClassName() [1/2]
|
inherited |
return the class name of the object
- Returns
- the class name of the object
References tString.
Referenced by CORE_Object::getIdentityString(), EMM_Operator::getName(), and CORE_Object::isMemoryChecked().

◆ getClassName() [2/2]
return the class name of the object
- Parameters
-
identityString the identity string of the object
- Returns
- the class name
◆ getDoubleEpsilon()
|
inlinestaticinherited |
get the epsilon value for tDouble type
- Returns
- the epsilon value for tDouble type
Referenced by CORE_Test::testType().
◆ getDoubleInfinity()
|
inlinestaticinherited |
get the infinity value for tFloat type
- Returns
- the intinity value for tFloat type
◆ getEpsilon()
|
inlinestaticinherited |
get the epsilon value for T type
- Returns
- the epsilon value for T type
◆ getFineElementsNumberPerCoarseElement()
|
inlineinherited |
get the number of elements of the fine grid per cell of the corse grid
- Returns
- the number of elements of the fine grid per cell of the corse grid
References EMM_MultiScaleGrid::mFineElementsNumberPerCoarseElement.
Referenced by EMM_MultiScaleCDGrid::meanValuesFromFineToCoarseGrid(), and meanValuesFromShiftFineGridToCoarseGrid().

◆ getFloatEpsilon()
|
inlinestaticinherited |
get the epsilon value for tFloat type
- Returns
- the epsilon value for tFloat type
Referenced by CORE_Test::testType().
◆ getFloatInfinity()
|
inlinestaticinherited |
get the infinity value for tFloat type
- Returns
- the intinity value for tFloat type
◆ getIdentityString()
|
inlineinherited |
return the identity string of the object of the form className_at_address
- Returns
- the identity string of the object
References CORE_Object::getClassName(), CORE_Object::pointer2String(), and tString.
Referenced by MATH_GaussLegendreIntegration::copy(), EMM_MultiScaleGrid::initialize(), CORE_Object::isInstanceOf(), CORE_Object::printObjectsInMemory(), MATH_Matrix::toString(), EMMG_SLPeriodicMultiScale::toString(), EMM_Stepper::toString(), EMM_AnisotropyDirectionsField::toString(), EMM_BlockMassMatrix::toString(), CORE_Object::toString(), EMM_Tensors::toString(), EMM_MultiScaleGrid::toString(), EMM_MatterField::toString(), EMM_Grid3D::toString(), and EMM_LandauLifschitzSystem::toString().

◆ getInfinity()
|
inlinestaticinherited |
get the infinity for T type
- Returns
- the infinity value for T type
◆ getLDoubleEpsilon()
|
inlinestaticinherited |
get the epsilon value for tLDouble type
- Returns
- the epsilon value for tLDouble type
Referenced by CORE_Test::testType().

◆ getLDoubleInfinity()
|
inlinestaticinherited |
get the infinity value for tDouble type
- Returns
- the infinity value for tDouble type
◆ getLevelComputationsNumber() [1/2]
|
inlineprotectedinherited |
return the number of calls of the level computations only for debug
- Returns
- the number of calls of the level computations only for debug
References EMM_MultiScaleGrid::mLevelComputationsNumber.
Referenced by EMM_MultiScaleCDGrid::addValuesFromCoarseGridToFinestGrid(), addValuesFromGridToZoneFinestGrid(), EMM_MultiScaleCDGrid::computeDemagnetizedExcitationFieldFromLevel(), computeZonalCenteredDemagnetizedFieldFromLevel(), and computeZonalDemagnetizedFieldAndNextLevelMagnetizationField().
◆ getLevelComputationsNumber() [2/2]
|
inlineprotectedinherited |
return the number of calls of the level computations only for debug
- Returns
- the number of calls of the level computations only for debug
References EMM_MultiScaleGrid::mLevelComputationsNumber, EMM_MultiScaleGrid::toString(), and tString.

◆ getLevelMagnetizationField()
|
inlineinherited |
get the magnetization field at level l
- Returns
- the magnetiaztion field at level l
Referenced by EMM_MultiScaleGrid::computeMultiGridExcitationField().

◆ getLevelsNumber()
|
inlineinherited |
get the leves number
- Returns
- the levels number
References EMM_MultiScaleGrid::mLevelsNumber.
Referenced by EMMG_SLRPPeriodicMultiScale::computeMultiGridExcitationField(), EMMG_SLSDXPeriodicMultiScale::computeMultiGridExcitationField(), and EMM_MultiScaleGrid::computeMultiGridExcitationField().

◆ getLevelUpMagnetizationField()
|
inlineinherited |
get the magnetization field at level l+1
- Returns
- the magnetiaztion field at level l+1
Referenced by EMM_MultiScaleGrid::computeMultiGridExcitationField().

◆ getMaxChar()
|
inlinestaticinherited |
get the max value for tChar type
- Returns
- the max value for tChar type
Referenced by CORE_Test::testType().

◆ getMaxDouble()
|
inlinestaticinherited |
get the max value for tDouble type
- Returns
- the max value for tDouble type
Referenced by CORE_Test::testType().
◆ getMaxFlag()
|
inlinestaticinherited |
get the max value for the tFlag type
- Returns
- the max value for the tFlag type
Referenced by CORE_Test::testType().

◆ getMaxFloat()
|
inlinestaticinherited |
get the max value for tFloat type
- Returns
- the max value for tFloat type
Referenced by CORE_Test::testType().
◆ getMaxIndex()
|
inlinestaticinherited |
get the max value for the array/vector indexing type
- Returns
- the max value for the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMaxInt()
|
inlinestaticinherited |
get the max value for tInt type
- Returns
- the max value for tInt type
Referenced by MATSGN_FFT::fastFourierTransform3D_FFTW(), and CORE_Test::testType().

◆ getMaxInteger()
|
inlinestaticinherited |
get the max value for the integer type
- Returns
- the max value for the integer type
Referenced by CORE_Test::testType().
◆ getMaxLDouble()
|
inlinestaticinherited |
get the max value for tLDouble type
- Returns
- the max value for tLDouble type
Referenced by CORE_Test::testType().
◆ getMaxLInt()
|
inlinestaticinherited |
get the max value for tLInt type
- Returns
- the max value for tLInt type
Referenced by CORE_Test::testType().

◆ getMaxLLInt()
|
inlinestaticinherited |
get the max value for tULInt type
- Returns
- the max value for tULInt type
Referenced by CORE_Test::testType().
◆ getMaxReal()
|
inlinestaticinherited |
get the max value for the real type
- Returns
- he max value for the real type
Referenced by EMM_MatterField::adimensionize(), and CORE_Test::testType().

◆ getMaxSInt()
|
inlinestaticinherited |
get the max value for tSInt type
- Returns
- the max value for tSInt type
Referenced by CORE_Test::testType().
◆ getMaxUChar()
|
inlinestaticinherited |
get the max value for tUChar type
- Returns
- the max value for tUChar type
Referenced by CORE_Test::testType().
◆ getMaxUIndex()
|
inlinestaticinherited |
get the max value for difference the array/vector indexing type
- Returns
- the max value for difference the array/vector indexing type
Referenced by CORE_Vector< T >::addAfterIndices(), CORE_Vector< T >::search(), CORE_Test::testType(), CORE_Integer::toHexString(), and CORE_Integer::toString().
◆ getMaxUInt()
|
inlinestaticinherited |
get the max value for tUInt type
- Returns
- the max value for tUInt type
Referenced by EMM_Array< tCellFlag >::loadFromFile(), EMM_RealField::loadFromFile(), and CORE_Test::testType().

◆ getMaxUInteger()
|
inlinestaticinherited |
get the max value for the unsigned integer type
- Returns
- the max value for the unsigned integer type
Referenced by MATH_Pn::computeExtrenums(), EMM_MultiScaleGrid::computeLevelsNumber(), EMM_Input::restoreBackup(), MATH_P0::solve(), and CORE_Test::testType().

◆ getMaxULInt()
|
inlinestaticinherited |
get the max value for tULInt type
- Returns
- the max value for tULInt type
Referenced by CORE_Test::testType().
◆ getMaxULLInt()
|
inlinestaticinherited |
get the max value for tULLInt type
- Returns
- the max value for tULLInt type
Referenced by CORE_Test::testType().
◆ getMaxUSInt()
|
inlinestaticinherited |
get the max value for tUSInt type
- Returns
- the max value for tUSInt type
Referenced by CORE_Test::testType().

◆ getMinChar()
|
inlinestaticinherited |
get the min value for tChar type
- Returns
- the min value for tChar type
Referenced by CORE_Test::testType().
◆ getMinDouble()
|
inlinestaticinherited |
get the min value for tDouble type
- Returns
- the min value for tDouble type
Referenced by CORE_Test::testType().

◆ getMinFlag()
|
inlinestaticinherited |
get the min value for the tFlag type
- Returns
- the min value for the tFlag type
Referenced by CORE_Test::testType().
◆ getMinFloat()
|
inlinestaticinherited |
get the min value for tFloat type
- Returns
- the min value for tFloat type
Referenced by CORE_Test::testType().
◆ getMinIndex()
|
inlinestaticinherited |
get the min value for the array/vector indexing type
- Returns
- the min value for the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMinInt()
|
inlinestaticinherited |
get the min value for tInt type
- Returns
- the min value for tInt type
Referenced by CORE_Test::testType().
◆ getMinInteger()
|
inlinestaticinherited |
get the min value for the integer type
- Returns
- the minin value for the integer type
Referenced by CORE_Test::testType().

◆ getMinLDouble()
|
inlinestaticinherited |
get the min value for tLDouble type
- Returns
- the min value for tLDouble type
Referenced by CORE_Test::testType().

◆ getMinLInt()
|
inlinestaticinherited |
get the min value for tLInt type
- Returns
- the min value for tLInt type
Referenced by CORE_Test::testType().
◆ getMinLLInt()
|
inlinestaticinherited |
get the min value for tLLInt type
- Returns
- the min value for tLLInt type
Referenced by CORE_Test::testType().

◆ getMinReal()
|
inlinestaticinherited |
get the min value for the real type
- Returns
- the min value for the real type
Referenced by CORE_Test::testType().
◆ getMinSInt()
|
inlinestaticinherited |
get the min value for tSInt type
- Returns
- the min value for tSInt type
Referenced by CORE_Test::testType().
◆ getMinUChar()
|
inlinestaticinherited |
get the min value for tUChar type
- Returns
- the min value for tUChar type
Referenced by CORE_Test::testType().
◆ getMinUIndex()
|
inlinestaticinherited |
get the min value for difference the array/vector indexing type
- Returns
- the min value for difference the array/vector indexing type
Referenced by CORE_Test::testType().
◆ getMinUInt()
|
inlinestaticinherited |
get the min value for tUInt type
- Returns
- the min value for tUInt type
Referenced by CORE_Test::testType().
◆ getMinUInteger()
|
inlinestaticinherited |
get the min value for the unsigned integer type
- Returns
- the min value for the unsigned integer type
Referenced by CORE_Test::testType().

◆ getMinULInt()
|
inlinestaticinherited |
get the min value for tULInt type
- Returns
- the min value for tULInt type
Referenced by CORE_Test::testType().

◆ getMinULLInt()
|
inlinestaticinherited |
get the min value for tULLInt type
- Returns
- the min value for tULLInt type
Referenced by CORE_Test::testType().
◆ getMinUSInt()
|
inlinestaticinherited |
get the min value for tUSInt type
- Returns
- the min value for tUSInt type
Referenced by CORE_Test::testType().
◆ getOut()
|
inlinestaticinherited |
◆ getPeriodicDirections() [1/2]
|
inlineinherited |
get the periodicity per direction
- Returns
- if the direction is periodic indexed by the index of the direction (x=0,y=1,z=2)
References EMM_MultiScaleGrid::mIsPeriodic.
Referenced by EMM_MultiScaleCDGrid::completeValuesOutsideFineGridByPeriodicityByExclusion(), EMMG_SLRPPeriodicMultiScale::computeMultiGridExcitationField(), EMMG_SLSDXPeriodicMultiScale::computeMultiGridExcitationField(), computeValuesOnShiftFineGrid(), and EMM_MultiScaleCDGrid::meanValuesFromFineToCoarseGrid().

◆ getPeriodicDirections() [2/2]
|
inlineinherited |
get the periodicity per direction
- Parameters
-
isXPeriodic : true if the x-direction is periodic isYPeriodic : true if the y-direction is periodic isZPeriodic : true if the z-direction is periodic
◆ getPointerAddress()
|
inlineinherited |
return the identity string of the object
- Returns
- the identity string of the object
References CORE_Object::pointer2String().

◆ getRealEpsilon()
|
inlinestaticinherited |
get the eps which is the difference between 1 and the least value greater than 1 that is representable.
- Returns
- the eps which is the difference between 1 and the least value greater than 1 that is representable.
Referenced by MATH_P4::solveP4De(), and CORE_Test::testType().
◆ getRealInfinity()
|
inlinestaticinherited |
get the infinity value
- Returns
- the inifinity value for the real type
Referenced by BrentFunction::BrentFunction(), EMM_OperatorsTest::compareDiscretizedData(), EMM_IterativeTimeStep::EMM_IterativeTimeStep(), EMM_SLElementaryDemagnetizedMatrix::Kxy(), NRFunction::NRFunction(), EMM_PolynomialInterpolationTimeStep::optimizeTimeFunction(), and CORE_Test::testType().
◆ getSegmentsNumber() [1/2]
|
inlineinherited |
get the segments number in all directions
- Parameters
-
Nx the segments number in x-direction Ny the segments number in y-direction Nz the segments number in z-direction
◆ getSegmentsNumber() [2/2]
|
inlineinherited |
get the segments number per dierction
- Returns
- the segments number by direction array indexed by the index of the direction (x=0,y=1,z=2)
References EMM_MultiScaleGrid::mN.
Referenced by EMM_MultiScaleCDGrid::addValuesFromCoarseGridToFinestGrid(), addValuesFromCoarseGridToFinestGrid(), addValuesFromShiftFineGridToFinestGrid(), EMM_MultiScaleCDGrid::completeValuesOutsideFineGridByPeriodicityByExclusion(), EMM_MultiScaleCDGrid::computeDemagnetizedExcitationFieldFromLevel(), EMMG_SLRPPeriodicMultiScale::computeMultiGridExcitationField(), EMMG_SLSDXPeriodicMultiScale::computeMultiGridExcitationField(), computeValuesOnShiftFineGrid(), computeZonalCenteredDemagnetizedFieldFromLevel(), computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), getShiftZone(), EMM_MultiScaleCDGrid::meanValuesFromFineToCoarseGrid(), meanValuesFromShiftFineGridToCoarseGrid(), EMM_MultiScaleCDGrid::resetValuesWithinCenteredZone(), and resetValuesWithinShiftZone().
◆ getSharedPointer() [1/2]
|
inlineinherited |
get the shared pointer of this class into p
- Parameters
-
p : shared pointer of the class This
Referenced by CORE_Map< Key, Value >::getSharedPointer(), CORE_ArrayList< tString >::getSharedPointer(), EMM_Array< tCellFlag >::getSharedPointer(), CORE_Array< tCellFlag >::getSharedPointer(), CORE_MorseArray< tUChar >::getSharedPointer(), CORE_Vector< T >::getSharedPointer(), and CORE_Object::printObjectsInMemory().
◆ getSharedPointer() [2/2]
|
inlineinherited |
get the shared pointer of this class into p
- Parameters
-
p : shared pointer of the class This
◆ getShiftZone() [1/2]
|
inlinestatic |
compute the shift zone
- Parameters
-
[in] Nx : number of segments in the x-direction [in] Ny : number of segments in the y-direction [in] Nz : number of segments in the z-direction [in] z : zone to compute the shift zone
- Returns
- the shift zone
| zone | shift zone | | 0 | 7 | | 1 | 6 | | 2 | 5 | | 3 | 4 | | 4 | 3 | | 5 | 2 | | 6 | 1 | | 7 | 0 |
References isZoneEmpty(), and tUCInt.
Referenced by computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), and getShiftZone().


◆ getShiftZone() [2/2]
compute the shift zone
- Parameters
-
[in] z : zone to compute the shift zone
- Returns
- the shift zone
| zone | shift zone | | 0 | 7 | | 1 | 6 | | 2 | 5 | | 3 | 4 | | 4 | 3 | | 5 | 2 | | 6 | 1 | | 7 | 0 |
References EMM_MultiScaleGrid::getSegmentsNumber(), getShiftZone(), and tUInteger.

◆ getThread()
|
inlinestaticinherited |
get the profilier
- Returns
- the profiler
Referenced by MATH_MaskVector::add(), MATH_Vector::add(), EMM_DisplacementFEMOperator::addBoundaryElasticStress(), EMM_DisplacementFEMOperator::buildDataOnNeumannBoundaryFaces(), EMM_DisplacementFVMOperator::computeCineticEnergy(), EMM_DisplacementFVMOperator::computeElasticStress(), EMM_DisplacementFEMOperator::computeElasticStress(), EMM_DisplacementFVMOperator::computeElasticTensor(), EMM_DisplacementFEMOperator::computeElasticTensor(), EMM_StaticMagneticTensorOperator::computeEnergy(), EMM_CubicAnisotropyOperator::computeEnergy(), EMM_MagnetostrictionOperator::computeEnergy(), EMM_DisplacementOperator::computeEnergy(), EMM_AnisotropyOperator::computeEnergyWithMagneticExcitation(), EMM_DisplacementFVMOperator::computeEquilibriumMatrixDiagonalConditioner(), EMM_DisplacementFEMOperator::computeEquilibriumMatrixDiagonalConditioner(), EMM_FullExchangeOperator::computeMagneticExcitationField(), EMM_StaticMagnetostrictionOperator::computeMagneticExcitationField(), EMM_LinearAnisotropyOperator::computeMagneticExcitationField(), EMM_StaticMagneticTensorOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationField(), EMM_MinimalExchangeOperator::computeMagneticExcitationField(), EMM_AnisotropyOperator::computeMagneticExcitationField(), EMM_MagnetostrictionOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_AnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_DisplacementFVMOperator::computeMagneticStress(), EMM_DisplacementFEMOperator::computeMagneticStress(), EMM_OptimalTimeStep::computeOptimalTimeStep(), EMM_DisplacementFEMOperator::computeStressConstraintEnergy(), EMM_FullExchangeOperator::discretize(), EMM_MinimalExchangeOperator::discretize(), EMM_CondensedMassMatrix::discretize(), EMM_LinearAnisotropyOperator::discretize(), EMM_AnisotropyOperator::discretize(), EMM_DemagnetizedOperator::discretize(), EMMG_SLDemagnetizedOperator::discretize(), EMM_LandauLifschitzSystem::discretize(), MATH_Vector::divide(), MATH_MaskVector::dot(), MATH_Vector::dot(), EMM_4SymmetricTensors::doubleDot(), EMM_4Tensors::doubleDotCrossDoubleDotScalar(), EMM_4Tensors::doubleDotCrossProduct(), EMM_4Tensors::doubleDotCrossSquaredScalar(), EMM_4Tensors::doubleDotProduct(), MATH_Vector::init(), MATH_MaskVector::init(), EMM_LandauLifschitzODE_RK::integrateMagnetizationFieldAtTime(), EMM_DisplacementFVM_Interpolator::interpolateUAtVertices(), EMMG_SLDemagnetizedOperator::localAssembly(), EMM_DisplacementOperator::nullProjectionOnDirichletBoundary(), EMM_DisplacementOperator::periodicProjection(), EMM_2PackedSymmetricTensors::product(), EMM_CanonicalMassMatrix::product(), MATH_FullMatrix::product(), EMM_CondensedMassMatrix::product(), EMM_BlockMassMatrix::product(), MATH_MorseMatrix::product(), EMMG_SLDemagnetizedOperator::product(), EMM_DisplacementOperator::projectionOnDirichletBoundary(), EMM_LandauLifschitzSystem::resetOperatorsToInitialState(), EMM_DisplacementFVMOperator::setBoundaryFaceTypes(), FFTW_MultiDFTs::setFFT(), FFTW_MultiLevelsDFT::setFFT(), FFTW_MultiLevelsDFT::setLevels(), FFTW_MultiDFTs::setPlan(), FFTW_MultiLevelsDFT::setPlan(), EMM_CondensedMassMatrix::solve(), EMM_LandauLifschitzODE::solveODE(), EMM_4SymmetricTensors::squaredDoubleDot(), EMM_4Tensors::squaredDoubleDotCrossScalar(), EMM_4Tensors::squaredDoubleDotScalar(), EMM_CanonicalMassMatrix::symmetricDot(), EMM_CondensedMassMatrix::symmetricDot(), EMM_BlockMassMatrix::symmetricDot(), FFTW_Test::test(), MATH_SolverTest::test(), EMM_ODETest::testODE(), and EMM_Grid3D::updateLimitConditionOnPoints().

◆ getToeplitzMatrix()
|
inlineinherited |
get the toeplitz matrix
- Returns
- the toeplitz matrix
Referenced by EMM_MultiScaleCDGrid::computeDemagnetizedExcitationFieldFromLevel(), EMMG_SLSDXPeriodicMultiScale::computeLevelDemagnetizedField(), EMMG_SLRPPeriodicMultiScale::computeMultiGridExcitationField(), EMM_MultiScaleGrid::computeMultiGridExcitationField(), computeZonalCenteredDemagnetizedFieldFromLevel(), and computeZonalDemagnetizedFieldAndNextLevelMagnetizationField().

◆ getTypeName()
|
inlinestaticinherited |
◆ getZonalMagnetizationField()
|
inlineinherited |
get the magnetization field at zone
- Returns
- the magnetiaztion field at zone
References EMM_MultiScaleGrid::computeMultiGridExcitationField(), EMM_MultiScaleGrid::computeZonalCenteredDemagnetizedFieldFromLevel(), EMM_MultiScaleGrid::computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), EMM_MultiScaleGrid::resetBlockValues(), tBoolean, tDimension, tReal, tUIndex, and tUInteger.
Referenced by EMM_MultiScaleGrid::computeMultiGridExcitationField(), and initialize().

◆ initialize()
|
virtual |
set the discretization
- Parameters
-
dim : dimension of the point Nx : number of segements along x-direction Ny : number of segements along y-direction Nz : number of segements along z-direction Px : periodicity along x-direction Py : periodicity along y-direction Pz : periodicity along z-direction l : number of levels
- initialize the fine grid bounds with a corse grid
- initialise the size of the M fields.
- compute the number of elements from the fine grid included in one element of the coarse grid.
Reimplemented from EMM_MultiScaleCDGrid.
References EMM_MultiScaleGrid::getZonalMagnetizationField(), EMM_MultiScaleCDGrid::initialize(), mTwoPowerZonalLevelsNumber, CORE_Object::out(), CORE_Out::println(), EMM_RealField::setDimension(), EMM_RealField::setSize(), and CORE_Integer::toString().
Referenced by New().

◆ is32Architecture()
|
inlinestaticinherited |
return true if the machine is a 32 bits machine
- Returns
- true is the computing is done in a 32 bits machine
References CORE_Object::pointer2String(), CORE_Object::printObjectsInMemory(), and tString.
Referenced by CORE_Test::testType().


◆ is64Architecture()
|
inlinestaticinherited |
return true if the machine is a 64 bits machine
- Returns
- true is the computing is done in a 64 bits machine
Referenced by EMM_VTK::getVTKType(), and CORE_Test::testType().
◆ isInstanceOf() [1/2]
|
inlineinherited |
test if the clas T is an instance of this class
- Returns
- true if the object is an instance of T
References null.
Referenced by MATH_ToeplitzTest::toeplitzTest().

◆ isInstanceOf() [2/2]
test if the object is an instance of className
- Parameters
-
name name of the class
- Returns
- true if the object is an instance of class Name
References CORE_Object::getIdentityString().

◆ isMemoryChecked()
|
inlinestaticinherited |
get if the memory checking is used
- Returns
- true: if the memory checking is used.
References CORE_Object::getClassName(), CORE_Object::mIsMemoryTesting, and tString.
Referenced by main().


◆ isZoneEmpty() [1/2]
|
inlinestatic |
return true if the zone is empty
- Parameters
-
[in] Nx : number of segments in the x-direction [in] Ny : number of segments in the y-direction [in] Nz : number of segments in the z-direction [in] z : zone to compute the shift zone
- Returns
- true if the zone is empty
the zone 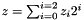 is empty if it exists i such that
is empty if it exists i such that 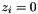 and
and 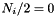
Referenced by computeValuesOnShiftFineGrid(), computeZonalCenteredDemagnetizedFieldFromLevel(), getShiftZone(), and EMM_DemagnetizedPeriodicalTest::shrinkingTest().

◆ isZoneEmpty() [2/2]
|
inlinestatic |
return true if the zone is empty
- Parameters
-
[in] N : number of segments per direction [in] z : zone to compute the shift zone
- Returns
- true if the zone is empty
the zone 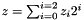 is empty if it exists i such that
is empty if it exists i such that 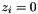 and
and 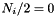
References addValuesFromCoarseGridToFinestGrid(), addValuesFromGridToZoneFinestGrid(), addValuesFromShiftFineGridToFinestGrid(), computeValuesOnShiftFineGrid(), computeZonalCenteredDemagnetizedFieldFromLevel(), computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), meanValuesFromShiftFineGridToCoarseGrid(), resetValuesWithinShiftZone(), tBoolean, tDimension, tInteger, tReal, tUCInt, tUIndex, and tUInteger.
◆ meanValuesFromFineToCoarseGrid()
|
inherited |
compute the field in a corse field from its fine grid.
- Parameters
the values of the field is meaned in the common part of the both grids as follow:
The values outside the fine grid 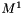 are set to 0 by defaut.
are set to 0 by defaut.
For each element of the fine grid (i,j,k), the corresponding element (I(i),J(j),K(k)) of the coarse grid is searched such that the center of the element (i,j,k) of the finest grid is inside the element (I,J,K) of the coarse grid.
The left boundary of the coarse grid is 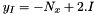 when the origin is at the center of the grid
when the origin is at the center of the grid
The center of the cell i of the fine grid is 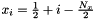 when the origin is at the center of the grid
when the origin is at the center of the grid
So, to search the cell of the coarse grid containing the center of the fine grid leads to 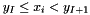 . We conclude that
. We conclude that
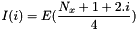
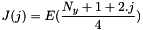
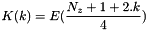 .
.
So than 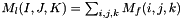 for all (i,j,k) such that I(i)=I, J(j)=J and K(k)=k
for all (i,j,k) such that I(i)=I, J(j)=J and K(k)=k
In the reverse way, we have 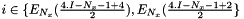 where
where 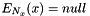 for
for 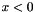 or
or 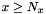 .
.
References EMM_MultiScaleGrid::getFineElementsNumberPerCoarseElement(), EMM_MultiScaleGrid::getPeriodicDirections(), EMM_MultiScaleGrid::getSegmentsNumber(), OMP_GET_THREAD_ID, OMP_GET_THREADS_NUMBER, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tBoolean, tDimension, tInteger, tReal, tUCInt, tUIndex, and tUInteger.
Referenced by EMM_MultiScaleCDGrid::computeMagnetizationFieldAtNextLevel(), and EMM_MultiScaleCDGrid::New().
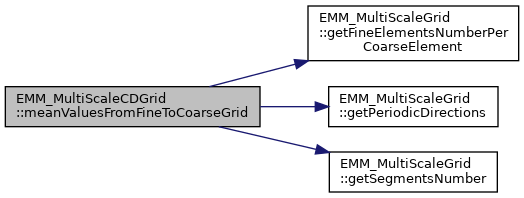

◆ meanValuesFromShiftFineGridToCoarseGrid()
| void EMM_MultiScaleSDGrid::meanValuesFromShiftFineGridToCoarseGrid | ( | const tUIndex & | nCells, |
| const tDimension & | dim, | ||
| const tUCInt & | z, | ||
| const tReal * | Mz, | ||
| tReal * | M | ||
| ) | const |
compute M at zone z of the coarse grid from the shift fine grid
- Parameters
-
[in] nCells : number of cells of the mesh [in] dim dimension of each point of the mesh [in] z zone of the grid [in] Mz magnetization values of size nCells x dim at zone z of the fine grid [out] M magnetization values of size nCells x dim at zone z of the coarse grid
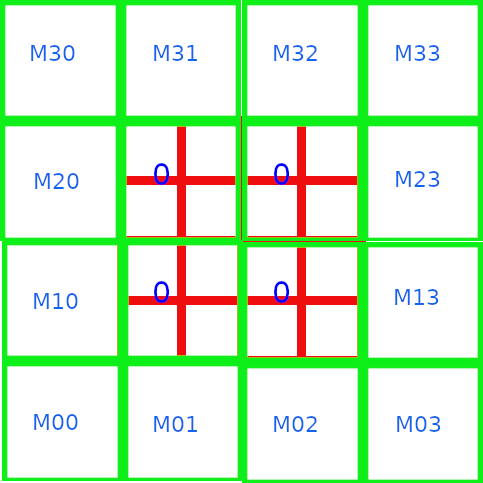 |
M at level l+1 built at zone z by computing of the mean of Mz within cells into coarse grid cells |
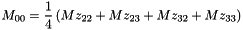
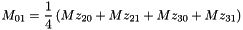
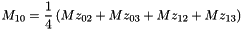
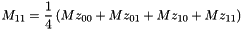
For each element of the shift fine grid (i,j,k), the corresponding element (I(i),J(j),K(k)) of the coarse grid is searched such that the center of the element (i,j,k) of the shift fine grid is inside the element (I,J,K) of the coarse grid.
The left boundary of the coarse grid is 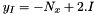 when the origin is at the center of the coarse grid and I in [0,Nx[ and step size of 1.
when the origin is at the center of the coarse grid and I in [0,Nx[ and step size of 1.
The center of the cell i of the shift fine grid is
- for zone 0 :
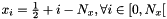
- for zone 1 :
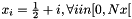
- for all zone :
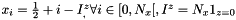
So, to search the cell of the coarse grid containing the center of cell of the shift fine grid leads to 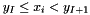 . We conclude that
. We conclude that
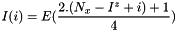
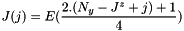
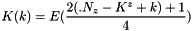 .
.
So than 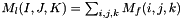 for all (i,j,k) such that I(i)=I, J(j)=J and K(k)=k
for all (i,j,k) such that I(i)=I, J(j)=J and K(k)=k
In the reverse way, we have 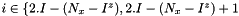 when I in [0,Nx/2[ or [Nx/2,Nx[ depending on zone.
when I in [0,Nx/2[ or [Nx/2,Nx[ depending on zone.
- for I in [0,Nx/2[,
- i=2.I, in [0,Nx[
- i=2.I+1 in [0,Nx[ for I in [Nx/2,Nx[
- i= 2.I - 2.(Nx/2) in [0,Nx[
- i= 2.I - 2.(Nx/2) + 1 in [0,Nx[
Note than 2.(Nx/2)=0 for Nx=1 which is a special case
The number w of fine grid cells in one cell of the corase grid is either 1 (segments number in each direction is 1) ,2 (only 1 direction with more than 2 segments) ,4 (only 1 direction with 1 segement) ,8 (all directions has more than 2 segments)
We have 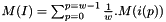 where i(p) is the index of the p-th cell in the shift fine grid.
where i(p) is the index of the p-th cell in the shift fine grid.
References EMM_MultiScaleGrid::getFineElementsNumberPerCoarseElement(), EMM_MultiScaleGrid::getSegmentsNumber(), null, OMP_GET_THREAD_ID, OMP_GET_THREADS_NUMBER, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tDimension, tInteger, tReal, tUCInt, tUIndex, tUInteger, and tUSInt.
Referenced by computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), and isZoneEmpty().

◆ New()
|
inlinestatic |
build a new instance of class
- Returns
- a shared pointer to This
References EMM_MultiScaleSDGrid(), initialize(), tBoolean, tDimension, and tUInteger.
Referenced by EMM_DemagnetizedPeriodicalTest::multiSDGridScaleTest(), and EMMG_ClassFactory::NewInstance().

◆ out()
|
inlinestaticinherited |
get the output
- Returns
- the output stream
Referenced by EMM_Matter::adimensionize(), EMM_DisplacementFVMOperator::backup(), EMM_DisplacementOperator::backup(), MATH_ElementaryMultiLevelsToeplitzMatrix::buildSpectralVectorProjector(), EMM_Test::caseTest(), EMM_Test::caseTests(), EMM_MatterField::computeAnisotropyDirectionsField(), EMM_OptimalTimeStep::computeOptimalTimeStep(), MATH_MultiLevelsToeplitzMatrix::copy(), CORE_Exception::CORE_Exception(), EMM_MatterField::createAnisotropyOperator(), CORE_Run::createIO(), EMM_ElementaryTest::defaultBackupTest(), EMM_ElementaryTest::defaultTest(), MATH_MultiLevelsFFTToeplitzMatrix::diagonalize(), EMM_DisplacementFVMOperator::discretize(), EMM_MagnetostrictionOperator::discretize(), EMM_DisplacementFEMOperator::discretize(), EMM_4SymmetricTensors::doubleDot(), EMM_4Tensors::doubleDotCrossDoubleDotScalar(), EMM_TensorsTest::doubleDotCrossDoubleDotScalarTests(), EMM_4Tensors::doubleDotCrossProduct(), EMM_TensorsTest::doubleDotCrossProductTests(), EMM_4Tensors::doubleDotCrossSquaredScalar(), EMM_TensorsTest::doubleDotCrossSquaredScalarTests(), EMM_4Tensors::doubleDotProduct(), EMM_TensorsTest::doubleDotProductTests(), EMM_DisplacementWaveTest::elasticWaveTest(), EMM_Test::elementaryTests(), FFTW_Test::fftwTutorial(), MATH_IntegrationTest::gaussLegendreTest(), EMM_MagnetostrictionTest::HComputingTest(), EMM_DemagnetizedPeriodicalTest::HTest(), EMMH_HysteresisTest::hysteresisDefaultCycleTest(), EMM_TensorsTest::initializationTests(), EMM_MultiScaleGrid::initialize(), initialize(), EMM_MatterField::loadFromANIFile(), EMM_AnisotropyDirectionsField::loadFromFile(), EMM_Matter::loadFromFile(), EMM_Grid3D::loadFromGEOFile(), EMM_MatterField::loadFromLOCFile(), EMM_Array< tCellFlag >::loadFromStream(), EMM_Matter::loadFromStream(), EMM_Matter::loadMattersFromFile(), EMM_Run::loadSystemFromOptions(), EMM_ElementaryTest::magnetostrictionBackupTest(), CORE_Run::make(), EMMH_Run::makeHysteresis(), EMM_Run::makeRun(), CORE_Run::makeType(), EMM_ElementaryTest::optionsTest(), MATH_PolynomialTest::P4Tests(), EMM_Test::primaryTests(), EMM_LandauLifschitzSystem::printLog(), CORE_Run::printOptions(), EMM_2PackedSymmetricTensors::product(), EMMG_SLDemagnetizedOperator::projectionOnSpectralSpace(), CORE_Run::readOptionsFromCommandLine(), CORE_Test::readVectorTest(), EMM_DemagnetizedPeriodicalTest::relaxationTest(), EMM_DisplacementFVMOperator::restore(), EMM_DisplacementOperator::restore(), EMM_Input::restoreBackup(), EMMH_Hysteresis::run(), EMM_Output::save(), EMM_AnisotropyDirectionsField::saveToFile(), EMM_MatterField::saveToFile(), EMM_Grid3D::saveToGEOFile(), CORE_IOTest::searchTest(), EMMH_Hysteresis::setInitialMagnetizationField(), MATH_MultiLevelsToeplitzMatrix::setLevels(), EMM_4SymmetricTensors::squaredDoubleDot(), EMM_4Tensors::squaredDoubleDotCrossScalar(), EMM_TensorsTest::squaredDoubleDotCrossScalarTests(), EMM_4Tensors::squaredDoubleDotScalar(), EMM_TensorsTest::squaredDoubleDotScalarTests(), EMM_TensorsTest::squaredDoubleDotTests(), EMM_MatterTest::testAdimensionize(), EMM_MatterTest::testANIFile(), CORE_Test::testComplex(), CORE_Test::testDateWeek(), FFTW_Test::testDFT(), EMM_MatterTest::testIO(), EMM_ODETest::testODE(), CORE_Test::testOut(), CORE_Test::testReal(), EMM_FieldTest::testRealArray(), EMM_Grid3DTest::testSegment(), EMM_Grid3DTest::testThinSheet(), CORE_Test::testTime(), CORE_Test::testType(), MATH_FullMatrix::toString(), EMM_DemagnetizedPeriodicalTest::xyPeriodicalCubeSDGTest(), and EMM_DemagnetizedPeriodicalTest::xyPeriodicalSheetSDGTest().

◆ pointer2String()
|
staticinherited |
return the string representation of a pointer
- Parameters
-
obj : oject to get the string pointer
- Returns
- the string pointer of the object
References tString.
Referenced by CORE_Object::CORE_Object(), CORE_Object::getIdentityString(), CORE_Object::getPointerAddress(), CORE_Object::is32Architecture(), and CORE_Object::~CORE_Object().

◆ printObjectsInMemory() [1/2]
|
staticinherited |
print object in memory
- Parameters
-
f : output to print the objects in memory
References CORE_Object::getIdentityString(), CORE_Object::getSharedPointer(), CORE_Object::mIsMemoryTesting, CORE_Object::mObjects, and tInteger.

◆ printObjectsInMemory() [2/2]
|
inlinestaticinherited |
print object in memory in the standart output
Referenced by CORE_Object::is32Architecture(), and main().
◆ resetBlockValues()
|
staticinherited |
reset the values in a block grid [iMin,iMax[x[jMin,jMax[x[kMin,kMax[ of dimension dim per point inside a grid of size [0,Nx[x[0,Ny[x[0,Nz[
- Parameters
-
[in] dim dimension of point [in] Nx : size of the grid in the x direction [in] Ny : size of the grid in the y direction [in] Nz : size of the grid in the z direction [in] iMin bounds if the block grid in [0,Nx[ [in] iMax bounds if the block grid in [0,Nx[ [in] jMin bounds if the block grid in [0,Ny[ [in] jMax bounds if the block grid in [0,Ny[ [in] kMin bounds if the block grid in [0,Nz[ [in] kMax bounds if the block grid in [0,Nz[ [in,out] M : field to reset values within the block grid
- Returns
- false if the block is empty
M is set to 0 on all points inside the grid [iMin,iMax[x[jMin,jMax[x[kMin,kMax[
References null, OMP_PARALLEL_PRIVATE_SHARED_DEFAULT, tReal, tUIndex, and tUInteger.
Referenced by EMM_MultiScaleGrid::getZonalMagnetizationField(), EMM_MultiScaleCDGrid::resetValuesWithinCenteredZone(), and resetValuesWithinShiftZone().

◆ resetOut()
|
inlinestaticinherited |
◆ resetThread()
|
inlinestaticinherited |
◆ resetValuesWithinCenteredZone()
|
inherited |
References EMM_MultiScaleGrid::getSegmentsNumber(), EMM_MultiScaleGrid::resetBlockValues(), tInteger, and tUInteger.
Referenced by EMM_MultiScaleCDGrid::completeValuesOutsideFineGridByPeriodicity(), EMM_MultiScaleCDGrid::computeDemagnetizedExcitationFieldFromLevel(), and computeZonalCenteredDemagnetizedFieldFromLevel().

◆ resetValuesWithinShiftZone()
| tBoolean EMM_MultiScaleSDGrid::resetValuesWithinShiftZone | ( | const tUIndex & | nCells, |
| const tDimension & | dim, | ||
| const tUCInt & | z, | ||
| tReal * | Mz | ||
| ) | const |
References EMM_MultiScaleGrid::getSegmentsNumber(), EMM_MultiScaleGrid::resetBlockValues(), tInteger, tUCInt, and tUInteger.
Referenced by computeZonalCenteredDemagnetizedFieldFromLevel(), computeZonalDemagnetizedFieldAndNextLevelMagnetizationField(), and isZoneEmpty().

◆ setIsMemoryChecked()
|
inlinestaticinherited |
set if the memory checking is used
- Parameters
-
v : true to check memory
Referenced by main().

◆ setOut()
|
inlinestaticinherited |
◆ setThis()
|
inlineprotectedinherited |
set this weak shared pointer called toDoAfterThis setting method
- Parameters
-
p : shared pointer of the class This
References CORE_Object::toDoAfterThisSetting().

◆ setThread()
|
inlinestaticinherited |
set the thread
- Parameters
-
thread the shared pointer to the thread
References null.
Referenced by EMM_Run::EMM_Run(), EMM_TensorsRun::EMM_TensorsRun(), and MATH_SolverRun::MATH_SolverRun().
◆ setToeplitzMatrix()
|
inlineinherited |
setthe toeplitz associated matrix
- Parameters
-
toeplitz the toeplitz matrix to set
References EMM_MultiScaleGrid::computeLevelsNumber(), EMM_MultiScaleGrid::initialize(), tBoolean, tDimension, and tUInteger.

◆ setZonalLevelsNumber()
|
inline |
set the number of levels with are divied in zones
- Parameters
-
[in] nLevels : number of levels with are divided in zones - if nLevels=0 => method is identically to CDG
- if nLevels >=1: SDG method on all levels l such that l <=nLevels.
◆ SP_OBJECT()
|
private |
◆ toDoAfterThisSetting()
|
inlineprotectedvirtualinherited |
method called after the setting of the shared pointer this method can only be called once.
Reimplemented from CORE_Object.
Reimplemented in EMM_DisplacementOperator, EMM_DisplacementFVMOperator, EMM_GaussLegendreRelaxation, and EMM_GradGaussLegendreRelaxation.
Referenced by EMM_GaussLegendreRelaxation::toDoAfterThisSetting(), and EMM_DisplacementOperator::toDoAfterThisSetting().

◆ toString()
|
virtualinherited |
return the class information in a tString
Reimplemented from CORE_Object.
Reimplemented in EMMG_SLPeriodicMultiScale.
References CORE_Object::getIdentityString().
Referenced by EMM_MultiScaleGrid::getLevelComputationsNumber().


Member Data Documentation
◆ Gamma
|
staticinherited |
◆ mHl
|
private |
◆ mTwoPowerZonalLevelsNumber
|
private |
◆ Mu0
|
staticinherited |
Referenced by EMM_MatterField::adimensionize(), EMM_MagnetostrictionOperator::adimensionize(), EMM_Matter::adimensionize(), EMM_CubicAnisotropyOperator::ComputeMagneticExcitation(), EMM_CubicAnisotropyOperator::computeMagneticExcitationField(), EMM_CubicAnisotropyOperator::computeMagneticExcitationFieldGradient(), EMM_CubicAnisotropyOperator::ComputeMagneticExcitationGradient(), EMM_Test::createMatters(), EMM_MatterField::getElasticTensorAdimensionizedParameter(), and EMM_MatterTest::testAdimensionize().
◆ NULL_VALUE
|
staticinherited |
Referenced by EMM_DisplacementFVM_VOGGROperator::computeGradAlmostNullUAtCellByOstrogradskiGreenIntegration(), EMM_DisplacementFVM_VTEGROperator::computeGradAlmostNullUAtCellByTaylorExpansionWithNeumannInterpolation(), EMM_DisplacementFVM_SSGROperator::computeGradAlmostNullUAtFaceByStokesIntegration(), EMM_DisplacementFVM_VOGGROperator::computeGradAlmostNullUAtNextCellByOstrogradskiGreenIntegration(), EMM_DisplacementFVM_VTEGROperator::computeGradUAtCellByTaylorExpansionWithNeumannInterpolation(), EMM_DisplacementFVM_VGROperator::computeGradUAtFace(), EMM_DisplacementFVM_SSGROperator::computeGradUAtFaceByStokesIntegration(), EMM_DisplacementFVM_STEGROperator::computeGradUAtFaceByTaylorExpansion(), EMM_DisplacementFVM_Interpolator::interpolateUAtEdge(), and EMM_DisplacementFVM_Interpolator::interpolateUAtVertices().
◆ SAVE_H_M_AT_LEVEL_1
|
staticinherited |
◆ X
|
staticinherited |
◆ Y
|
staticinherited |
Referenced by EMMG_SLSDXPeriodicMultiScale::computeMultiGridExcitationField(), EMMG_RealField::fitToSize(), EMM_MassMatrix::getElementVolume(), EMM_CanonicalMassMatrix::isSymmetric(), EMM_BlockMassMatrix::product(), EMM_CondensedMassMatrix::product(), EMM_RealField::setValue(), EMM_CanonicalMassMatrix::solve(), EMM_BlockMassMatrix::solve(), EMM_BlockMassMatrix::toString(), and EMMG_RealField::wedge().
◆ Z
|
staticinherited |
The documentation for this class was generated from the following files:
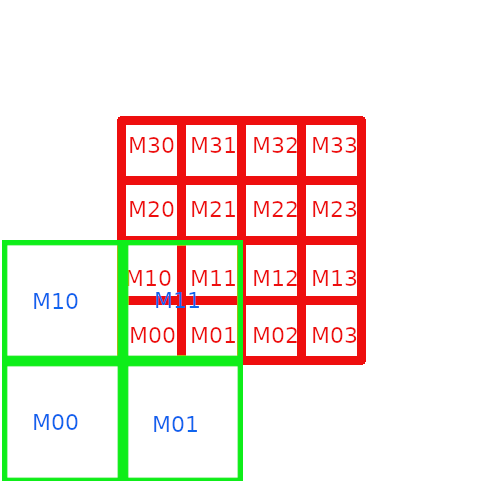
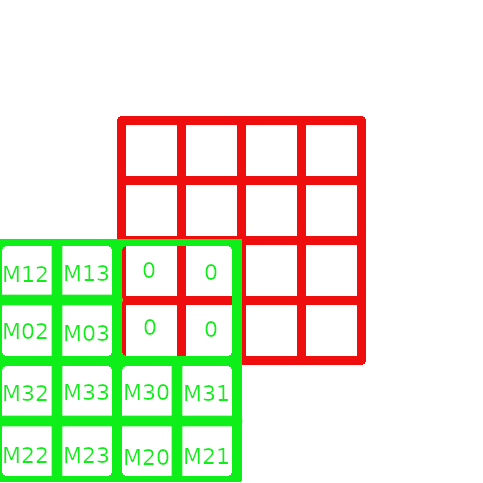
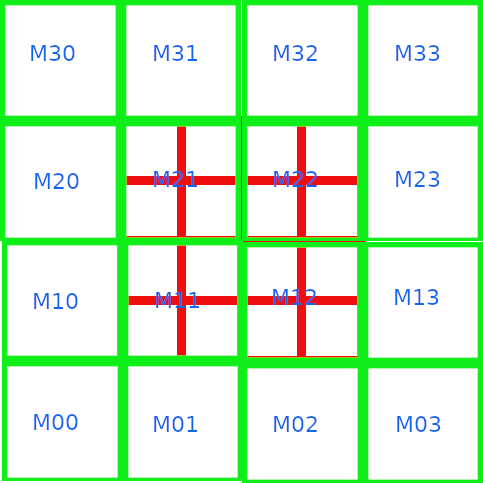
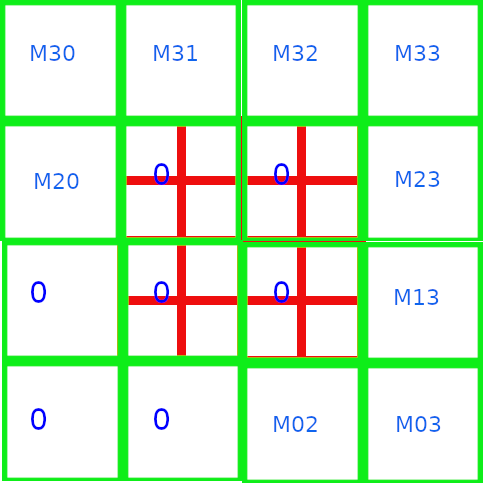
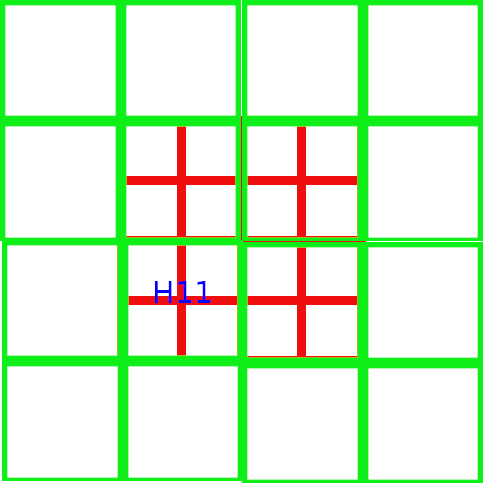
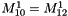
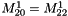
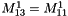
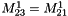
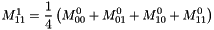
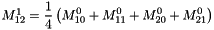
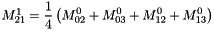
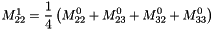


 1.8.13
1.8.13