My home page
Here you will find some
information on my scientific activities as
professor of Applied Mathematics in Jean Kuntzmann Lab
of Grenoble Institute of Technology of Grenoble Alpes University.

Who am i?
Applied mathematician, my research affiliation is the Partial Differential Equations team of the Jean Kuntzmann Lab, and I mainly teach in Ensimag, Grenoble Institute of Technology. My fields of research are mathematical and numerical analysis of PDE.

What I Do?
Level set methods
I got interested in developing new methods to capture interfaces while recording mechanical properties. Applications are in fluid structure coupling with a particular emphasis on modeling of red blood cells. I co-authored a book on that subject.
Optimal transport
I worked on efficient algorithms for dynamic optimal transport and studied some of their analytical properties with Romain Hug and Nicolas Papadakis.
Partial differential equations
Mainly around doubly nonlinear elliptic-parabolic equations and transport equations.
Publications on level-set methods
[1] Thibaut Metivet, Arnaud Sengers, Mourad Ismail, Emmanuel Maitre. Diffusion–redistanciation schemes for 2D and 3D constrained Willmore flow: application to the equilibrium shapes of vesicles. Journal of Computational Physics, Elsevier, 2021.
[2] Georges–Henri Cottet, Emmanuel Maitre, Thomas
Milcent. Formulation Eulerienne et méthodes level set
pour des problèmes d’interaction
fluide–structure. Mathématiques et applications,
Springer, 2021.
[3] Meriem Jedouaa, Charles–Henri Bruneau, Emmanuel Maitre. An efficient interface capturing method for a large collection of interacting bodies immersed in a fluid. Journal of Computational Physics, Elsevier, 2019, 378, pp.143–177.
[4] Georges–Henri Cottet, Emmanuel Maitre. A semi–implicit level set method for multiphase flows and fluid–structure interaction problems. Journal of Computational Physics, Elsevier, 2016, 314, pp.80–92.
[5] Thomas Milcent, Emmanuel Maitre. Eulerian model of immersed elastic surfaces with full membrane elasticity. Communications in Mathematical Sciences, International Press, 2016, 14 (3), pp.857–881.
[6] Nicolas James, Emmanuel Maitre, Iraj Mortazavi. Immersed boundary methods for the numerical simulation of incompressible aerodynamic and fluid–structure interactions. Annales mathématiques Blaise Pascal, cedram, 2013, 20 (1), pp.139–173.
[7] Emmanuel Maitre, Chaouqi Misbah, Philippe Peyla, Annie Raoult. Comparison between advected–field and level–set methods in the study of vesicle dynamics. Physica D: Nonlinear Phenomena, Elsevier, 2012, 241 (2012), pp.1146–1157.
[8] Claire Bost, Georges–Henri Cottet, Emmanuel Maitre. Convergence analysis of a penalization method for the three–dimensional motion of a rigid body in an incompressible viscous fluid. SIAM Journal on Numerical Analysis, Society for Industrial and Applied Mathematics, 2010, 48 (4), pp.1313–1337.
[9] Emmanuel Maitre, Thomas Milcent, Georges–Henri Cottet, Annie Raoult, Yves Usson. Applications of level set methods in computational biophysics. Mathematical and Computer Modelling, Elsevier, 2009, 49 (11–12), pp.2161–2169.
[10] Georges–Henri Cottet, Emmanuel Maitre, Thomas Milcent. Eulerian formulation and level set models for incompressible fluid–structure interaction. ESAIM: Mathematical Modelling and Numerical Analysis, EDP Sciences, 2008, 42 (3), pp.471–492.
[11] Emmanuel Maitre, Fadil Santosa. Level set methods for optimization problems involving geometry and constraints II. Optimization over a fixed surface. Journal of Computational Physics, Elsevier, 2008, 227 (22), pp.9596–9611.
[12] Emmanuel Maitre, Patrick Witomski. Transport equation with boundary conditions for free surface localization. Numerische Mathematik, Springer Verlag, 1999, 84 (2), pp.275–303.
[13] Georges–Henri Cottet, Emmanuel Maitre. A level set method for fluid–structure interactions with immersed surfaces. Mathematical Models and Methods in Applied Sciences, World Scientific Publishing, 2006, 16, pp.415–438.
Publications on optimal transport
[1] Romain Hug, Emmanuel Maitre, Nicolas Papadakis. On the convergence of augmented Lagrangian method for optimal transport between nonnegative densities. Journal of Mathematical Analysis and Applications, Elsevier, 2020, 485 (2), pp.123811.
[2] Morgane Henry, Emmanuel Maitre, Valérie Perrier. Primal–dual formulation of the Dynamic Optimal Transport using Helmholtz–Hodge decomposition. 2019.
[3] Romain Hug, Emmanuel Maitre, Nicolas Papadakis. Multi–physics Optimal Transportation and Image Interpolation. ESAIM: Mathematical Modelling and Numerical Analysis, EDP Sciences, 2015, Special Issue – Optimal Transport, 49 (6), pp.1671–1692.
[4] Morgane Henry, Emmanuel Maitre, Valérie Perrier. Optimal Transport using Helmholtz–Hodge Decomposition and First–Order Primal–Dual Algorithms. 2015 IEEE International Conference on Image Processing (ICIP), Sep 2015, Quebec City, QC, Canada. pp.4748–4752,
[5] Damiano Lombardi, Emmanuel Maitre. Eulerian models and algorithms for unbalanced optimal transport. ESAIM: Mathematical Modelling and Numerical Analysis, EDP Sciences, 2015, Special Issue – Optimal Transport, 49 (6), pp.1717–1744.
Publications on PDE
[1] Stéphane Labbé, Emmanuel Maitre. A free boundary model for
Korteweg fluids as a limit of barotropic compressible
Navier–Stokes equations. Methods and Applications of
Analysis, 2013, 20 (2), pp.165–178.
[2] Emmanuel Maitre. On a nonlinear compactness lemma in
Lp(0,T;B). International Journal of Mathematics and
Mathematical Sciences, 2003, vol. 2003, no 27,
p. 1725-1730.
[3] Emmanuel Maitre. Numerical analysis of nonlinear
elliptic-parabolic equations. ESAIM: Mathematical
Modelling and Numerical Analysis-Modélisation
Mathématique et Analyse Numérique, 2002, vol. 36, no
1, p. 143-153.
[4] Samir Akesbi, Emmanuel Maitre. Theoretical and numerical analysis of a minimal residual solver for 2D Boltzmann transport equation. Journal of computational and applied mathematics, 2003, vol. 150, no 2, p. 357-374.
[5] Emmanuel Maitre, Patrick Witomski. A pseudo–monotonicity
adapted to doubly nonlinear elliptic–parabolic equations. Nonlinear
Analysis: Theory, Methods and Applications, Elsevier, 2002, 50 (2),
pp.223–250.
[6] Samir Akesbi, Emmanuel Maitre. Minimal residual method applied to the transport equation. Numerical Algorithms, 2001, vol. 26, no 3, p. 235-249.
My lectures
Mathematical Analysis
1st year Ensimag
Variational methods applied to modelling
2nd year Ensimag / MSIAM 1
Level set and optimisation methods for image analysis
3rd year Ensimag / MSIAM M2
RESSOURCES
- Active contour using the level-set method : notes and notebook to download.
- Primal-dual algorithm and applications : notebook to download.
- Optimal transport : generic
case and lab on obstacle problems.
ARTIClES FOR ORAL PRESENTATION
Note: You are supposed to choose one of those, email me your choice (on a first arrived / first served basis). Alternatively, you could find an article (e.g. on google scholar) in link with the lecture, and of course email me about that.
Articles on Level-set method / contouring methods
- Image segmentation using a multilayer level-set approach, Ginmo Chung et Luminita A. Vese, Comput Visual Sci (2009).
- Active contours without level sets, R Yildizoglu, JF Aujol, N Papadakis - Proc. ICIP'12 (2012).
- Mumford–Shah based registration: a comparison of a level set and a phase field approach, M. Droske, W. Ring, M. Rumpf, Comput Visual Sci (2009)
- Adaptive level set evolution starting with a constant function, Yan Wang, Chuanjiang He, Applied Mathematical Modelling (2012)
- A Level-Set Method Based on Global and Local Regions for Image Segmentation, ZHAO, Yu Qian, WANG, Xiao Fang, SHIH, Frank Y., et al. International Journal of Pattern Recognition and Artificial Intelligence, 2012, vol. 26, no 01.
- Robust segmentation of overlapping cells in histopathology specimens using parallel seed detection and repulsive level set, QI, Xin, XING, Fuyong, FORAN, David J., et al. Biomedical Engineering, IEEE Transactions on, 2012, vol. 59, no 3, p. 754-765.
- Level set evolution with locally linear classification for image segmentation, WANG, Ying, XIANG, Shiming, PAN, Chunhong, et al. Pattern Recognition, 2012.
- Detection of the whole myocardium in 2D-echocardiography for multiple orientations using a geometrically constrained level-set, DIETENBECK, Thomas, ALESSANDRINI, Martino, BARBOSA, Daniel, et al. Medical Image Analysis, 2012, vol. 16, no 2, p. 386-401.
- Multi-object spring level sets (MUSCLE), LUCAS, Blake C., KAZHDAN, Michael, et TAYLOR, Russell H. In : Medical Image Computing and Computer-Assisted Intervention–MICCAI 2012. Springer Berlin Heidelberg, 2012. p. 495-503.
- Active contours for multi-region image segmentation with a single level set function, DUBROVINA, Anastasia, ROSMAN, Guy, et KIMMEL, Ron. In : Scale Space and Variational Methods in Computer Vision. Springer Berlin Heidelberg, 2013. p. 416-427.
- ORACM: Online Region-Based Active Contour Model, FATIH TALU, M. Expert Systems with Applications 40 (2013) 6233–6240.
- Image Gradient Based Level Set Methods in 2D and 3D, XIE, Xianghua, YEO, Si Yong, MIRMEHDI, Majid, et al. In : Deformation Models. Springer Netherlands, 2013. p. 101-120.
- Active contour model driven by local histogram fitting energy,LIU, Weiping, SHANG, Yanfeng, et YANG, Xin. Pattern Recognition Letters 34 (2013) 655–662.
- A multiple object geometric deformable model for image segmentation, John A. Bogovic, Jerry L. Prince, Pierre-Louis Bazin, Computer Vision and Image Understanding, Volume 117, Issue 2, February 2013, Pages 145-157.
- A local region-based Chan–Vese model for image segmentation, LIU, Shigang et PENG, Yali. Pattern Recognition, 2012, vol. 45, no 7, p. 2769-2779.
- Vector-Valued Image Processing by Parallel Level Sets., EHRHARDT, M. et ARRIDGE, Simon R. IEEE TRANSACTIONS ON IMAGE PROCESSING, 2013.
- Graph Cut Optimization for the Piecewise Constant Level Set Method Applied to Multiphase Image Segmentation, Egil Bae and Xue-Cheng Tai, Lecture Notes in Computer Science (2009).
- A Review of Statistical Approaches to Level Set Segmentation: Integrating Color, Texture, Motion and Shape, D. Cremers et al, International Journal of Computer Vision (2007).
- Combinatorial Optimization of the piecewise constant Mumford-Shah functional with application to scalar/vector valued and volumetric image segmentation, Noha El-Zehiry, Prasanna Sahoo, Adel Elmaghraby, Image and Vision Computing (2011).
- Four-Color Theorem and Level Set Methods for Watershed Segmentation, Erlend Hodneland, Xue-Cheng Tai, Hans-Hermann Gerdes, Int J Comput Vis (2009).
- Active contours with selective local or global segmentation: A new formulation and level set method, Kaihua Zhang, Lei Zhang, Huihui Song, Wengang Zhou, Image and Vision Computing (2010).
- Segmentation of interest region in medical volume images using geometric deformable model, Myungeun Lee, Wanhyun Cho, Sunworl Kim, Soonyoung Park, Jong Hyo Kim, Computers in Biology and Medicine (2012).
- Fast and Robust Clinical Triple-Region Image Segmentation Using One Level Set Function, Shuo Li1, Thomas Fevens, Adam Krzyzak, Chao Jin, and Song Li, Lecture Notes in Computer Science (2006).
- Tensor diffusion level set method for infrared targets contours extraction, Meng Li, Chuanjiang He, Yi Zhan, Infrared Physics & Technology (2012).
- A Binary Level Set Model and some Applications to Mumford-Shah Image Segmentation, Johan Lie, Marius Lysaker and Xue-Cheng Tai, IEEE Transactions on Image Processing (2006).
- Colour, texture, and motion in levelset based segmentation and tracking, Thomas Broxa, Mikaël Roussonb, Rachid Derichec, Joachim Weickert, Image and Vision Computing (2010).
- A high-throughput active contour scheme for segmentation of histopathological imagery, Jun Xu, Andrew Janowczyk, Sharat Chandran, Anant Madabhushi, Medical Image Analysis (2011).
- An overview of the Mumford-Shah problem, Milan J. Math (2003).
Articles Level-set / other applications than image
- A level-set approach for inverse problems involving obstacles, SANTOSA Fadil, COCV 1996.
- A Simple Level Set Method for Solving Stefan Problems, S. Chen, B. Merriman, S. Osher, and P. Smereka, Journal of Computational Physics, 135, 8–29 (1997)
- Fast Surface Reconstruction Using the Level Set Method, Hong-Kai Zhao, Stanley Osher, Ronald Fedkiw, In Variational and Level Set Methods in Computer Vision, 2001. Proceedings. IEEE Workshop on (pp. 194-201). **[Michael Bleuez and Nicolas Cavaillès--Wurmser]**
- Structural optimization using sensitivity analysis and a level-set method, Gr egoire Allaire, François Jouve et Anca-Maria Toader, Journal of Computational Physics 194 (2004) 363--393
- A new hole insertion method for level set based structural topology optimization, DUNNING, Peter D. et ALICIA KIM, H. International Journal for Numerical Methods in Engineering, 2013, vol. 93, no 1, p. 118-134.
- A topology optimization method based on the level set method incorporating a fictitious interface energy, YAMADA, Takayuki, IZUI, Kazuhiro, NISHIWAKI, Shinji, et al. Computer Methods in Applied Mechanics and Engineering, 2010, vol. 199, no 45, p. 2876-2891.
- A new method for the level set equation using a hierarchical-gradient truncation and remapping technique, KOHNO, Haruhiko et NAVE, Jean-Christophe. Computer Physics Communications 184 (2013) 1547–1554.
- A Real-Time Algorithm for the Approximation of Level-Set-Based Curve Evolution, IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 17, NO. 5, MAY 2008.
- Modeling holes and inclusions by level sets in the extended nite-element method, Natarajan Sukumar, David Chopp, Nicolas Moës, Ted Belytschko, 2001.
- Snakes: Active Contour Models, MICHAEL KASS, ANDREW WITKIN, and DEMETRI TERZOPOULOS, 1988.
- A FAST SWEEPING METHOD FOR EIKONAL EQUATIONS, HONGKAI ZHAO, 2004.
- Fully implicit methodology for the dynamics of biomembranes and capillary interfaces by combining the level set and Newton methods, Aymen Laadhari et al, 2016
Articles on seismic imaging and geophysics applications of OT
- Analysis of optimal transport and related misfit functions in FWI, Yunan Yang and Björn Engquist, proc. SEG International Exposition and 87th Annual Meeting, 2017.
- An optimal transport approach for seismic tomography: Application to 3D full waveform inversion, L. Métivier, R. Brossier, Q. Mérigot, E. Oudet, J. Virieux, submitted, 2016
- OPTIMAL TRANSPORT FOR SEISMIC FULL WAVEFORM INVERSION, Björn Engquist, Brittany Froese, Yunan Yang, 2016
- Measuring the misfit between seismograms using an optimal transport distance: Application to full waveform inversion, L. Métivier, R. Brossier, Q. Mérigot, E. Oudet, J. Virieux, 2015.
- An introduction to full waveform inversion, J. Virieux et al. (2015)
- APPLICATION OF THE WASSERSTEIN METRIC TO SEISMIC SIGNALS,Björn Engquist, Brittany Froese, 2013.
- An overview of full-waveform inversion in exploration geophysics, J. Virieux and S. Operto, 2009
Articles on optimal transport
- Regularized discrete optimal transport, Ferradans, S., Papadakis, N., Rabin, J., Peyré, G., & Aujol, J. F., in Scale Space and Variational Methods in Computer Vision Volume 7893 of the series Lecture Notes in Computer Science pp 428-439. Springer Berlin Heidelberg. 2013.
- Texture Mapping via Optimal Mass Transport, Ayelet Dominitz, Allen Tannenbaum, IEEE Trans Vis Comput Graph. (2010)
- An efficient numerical algorithm for the L2 optimal transport problem with periodic densities, SAUMIER, Louis-Philippe, AGUEH, Martial, et KHOUIDER, Boualem. IMA Journal of Applied Mathematics, 2013, p. 1-23.
- From Knothe's rearrangement to Brenier's optimal transport map, BONNOTTE, Nicolas. SIAM Journal on Mathematical Analysis, 2013, vol. 45, no 1, p. 64-87.
- Wasserstein active contours, PEYRÉ, Gabriel, FADILI, Jalal, et RABIN, Julien. In : Image Processing (ICIP), 2012 19th IEEE International Conference on. IEEE, 2012. p. 2541-2544.
- Variational Earth Mover's Distance for Image Segmentation, LI, Peihua et WANG, Qilong. In : Image and Graphics (ICIG), 2013 Seventh International Conference on. IEEE, 2013. p. 236-242.
- An Efficient Numerical Method for the Solution of the L_2 Optimal Mass Transfer Problem, Eldad Haber, Tauseef Rehman, and Allen Tannenbaum, SIAM J Sci Comput. (2010) .
- Image Sequence Interpolation Based on Optical Flow,
Segmentation, and Optimal Control, Kanglin Chen and Dirk A. Lorenz, IEEE Transactions on Image Processing (2012).
- Geodesic Shape Retrieval via Optimal Mass Transport, Julien Rabin, Gabriel Peyré, and Laurent D. Cohen, 11th European Conference on Computer Vision, Heraklion, Crete : Greece (2010).
Modelling seminar and projects
MSIAM M2
what i’ve worked on?

Rat cardiomyocyte modelling
With biologists from the TIMC Lab we modelled the calcium waves propagation on rat cardiomyocytes.
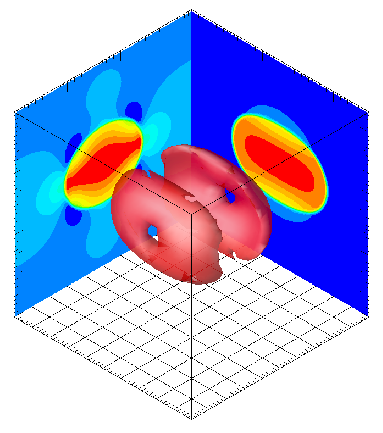
Immersed elastic membrane
With Georges-Henri Cottet we built a level set formulation of the immersed boundary method.
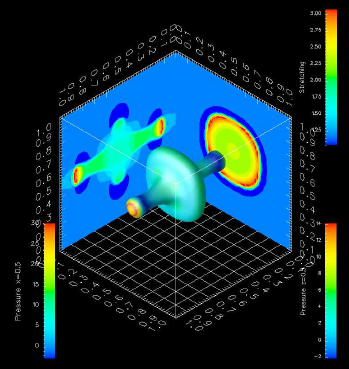
Level set method on surfaces
With Fadil Santosa we studied the isoperimetric problem on surface using the level set method.

Fabrics modelling
With Nadjombé Faré we studied the draping problem while I was assistant professor in Mulhouse.
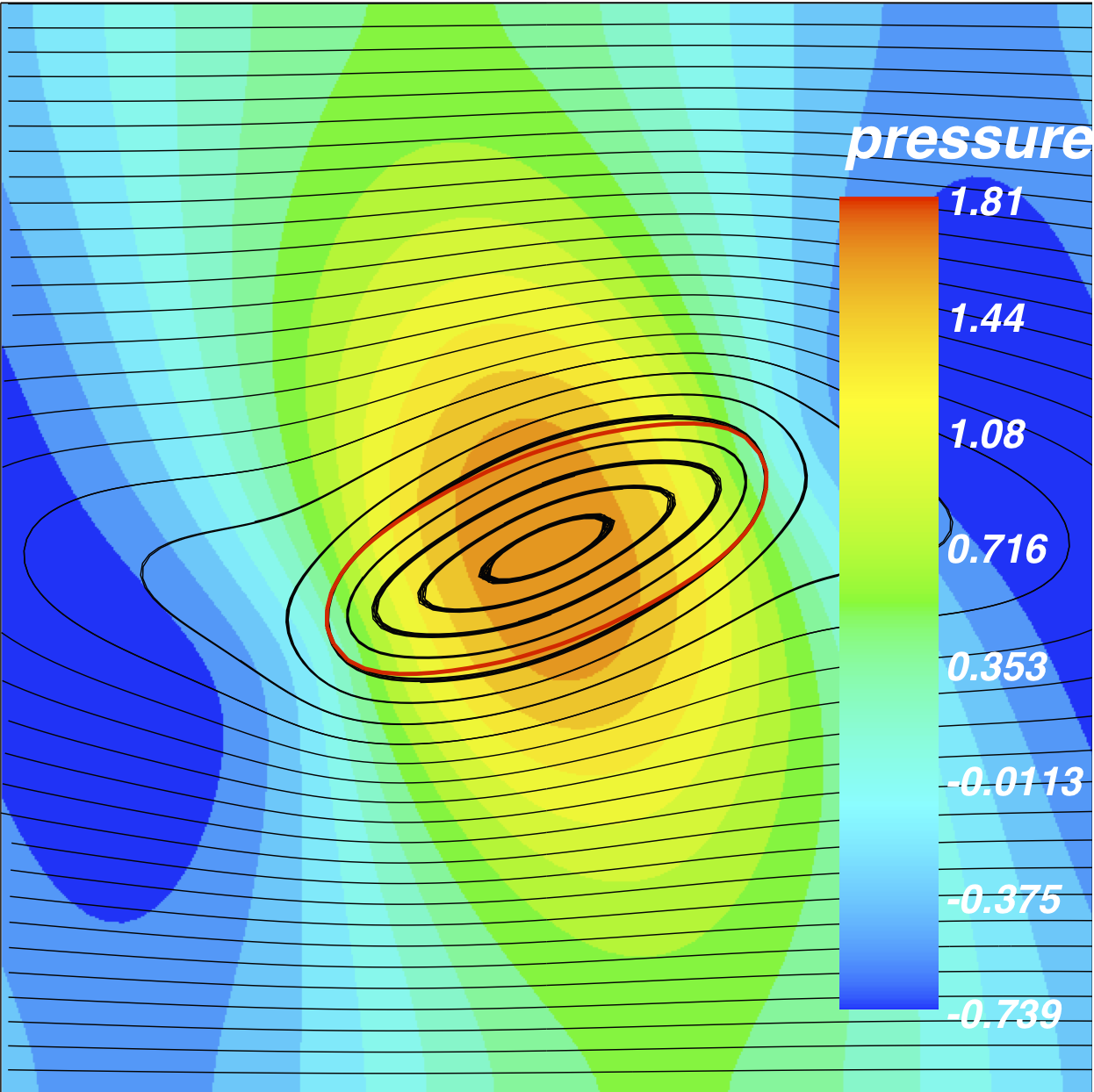
Parametric instability of membrane
This instability is observed in the Leidenfrost phenomenom and is driven by a variation of surface stiffness.
Tank-treading motion of vesicle
Phospholipidic vesicles are models of red blood cells that undergo complex behavio in shear flow, that we studied with Physicists of LiPhy Lab.
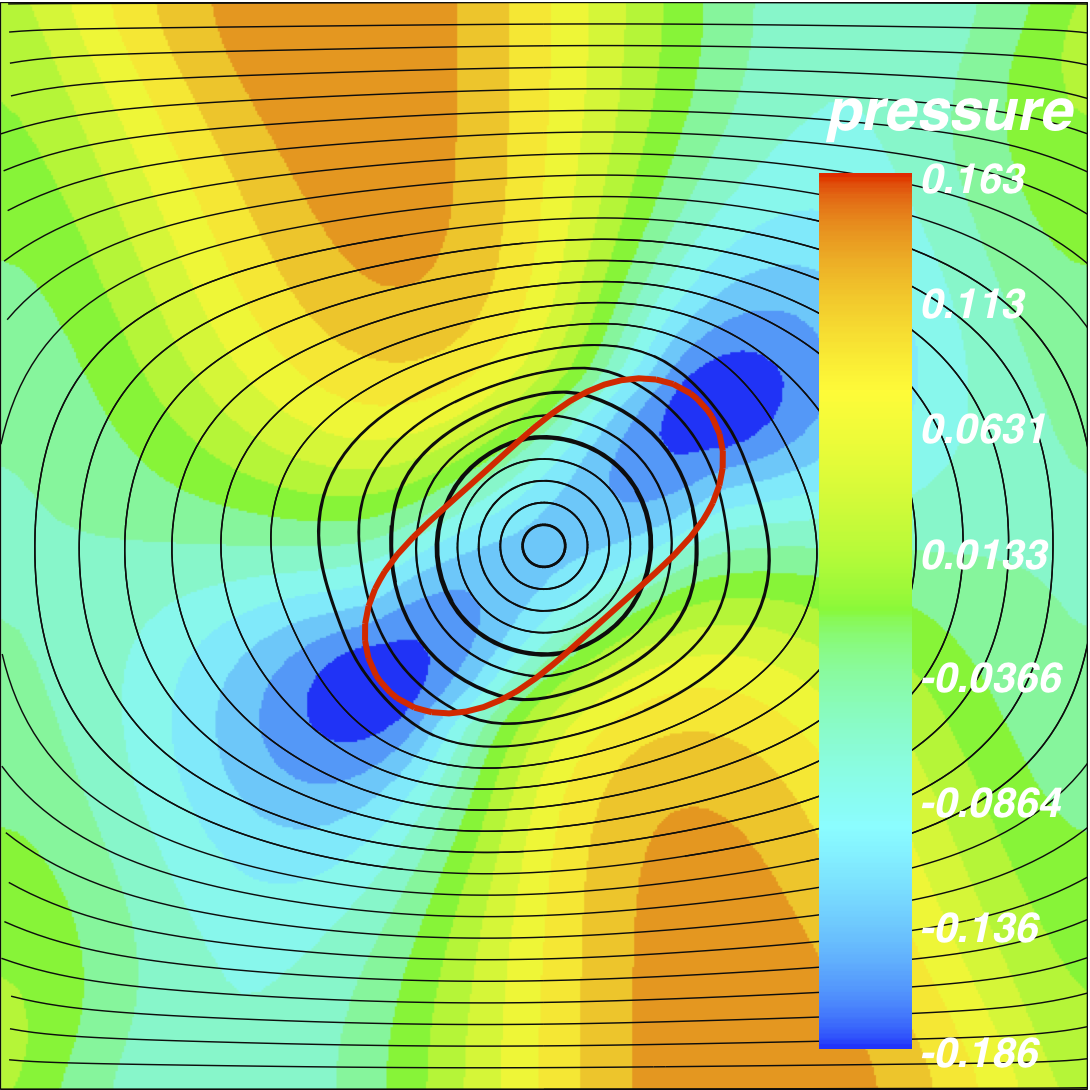
Tumbling motion of vesicle
Phospholipidic vesicles are models of red blood cells that undergo complex behavio in shear flow, that we studied with Physicists of LiPhy Lab.
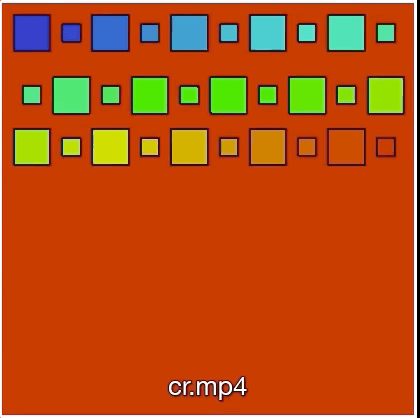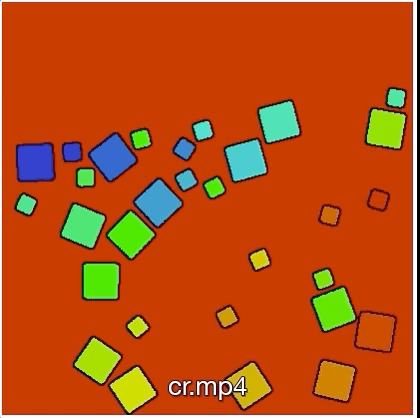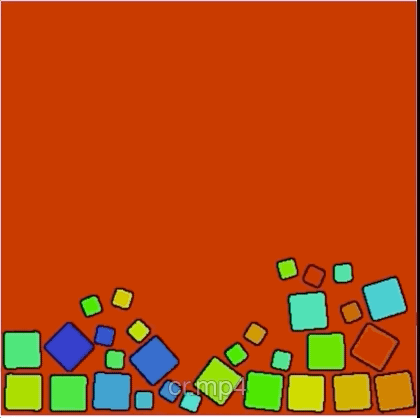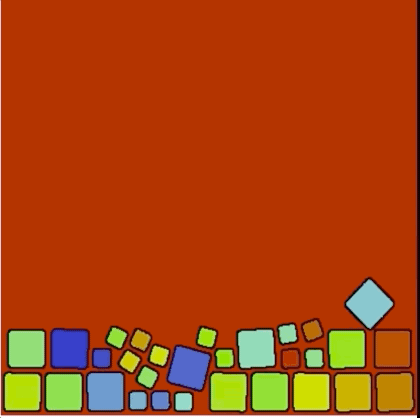
Contact forces handling
With Meriem Jedouaa and Charles-Henri Bruneau we deviced an efficient method to efficiently handle interactions of many immersed objects in an Eulerian context. .
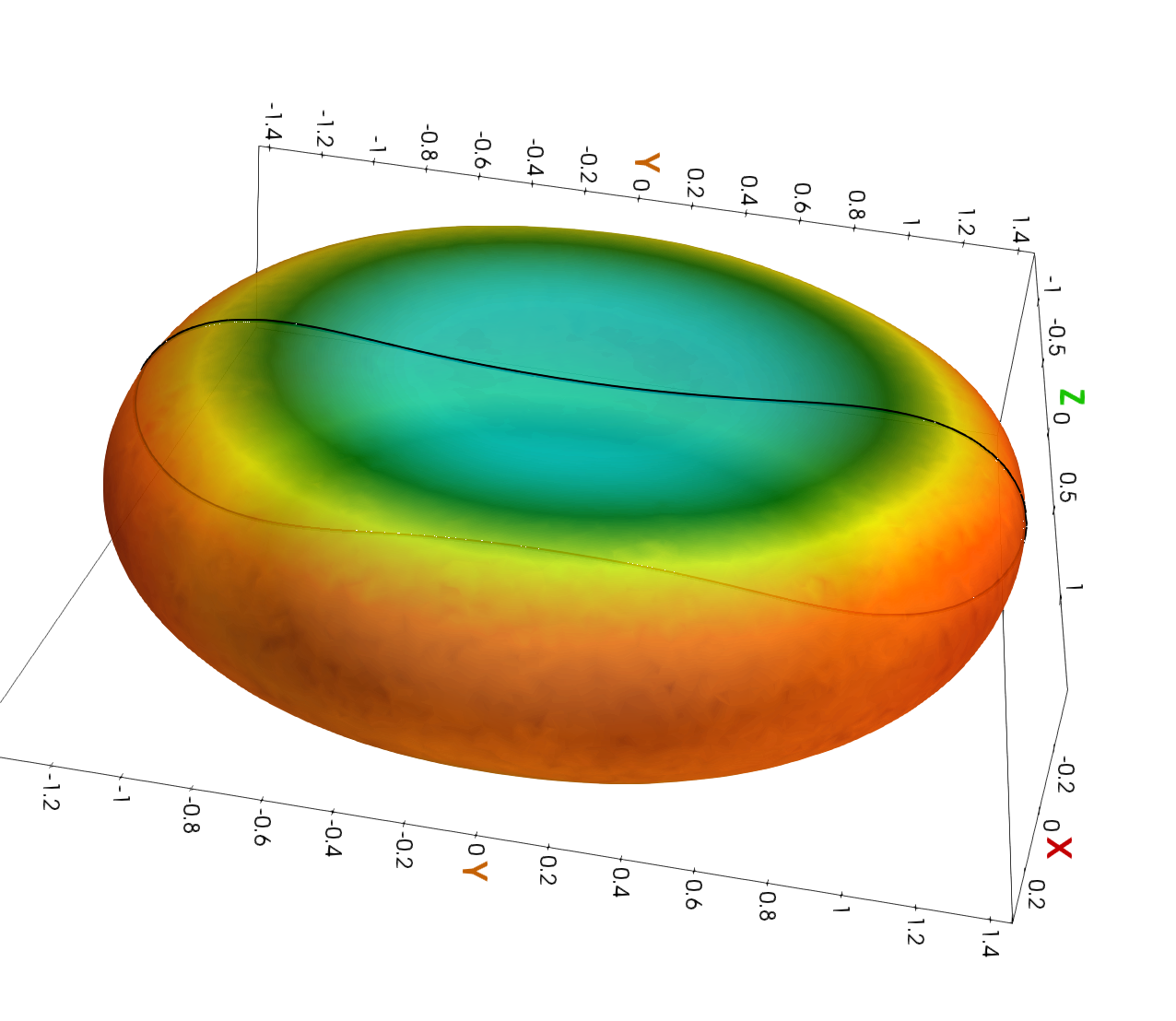
Vesicle shape computation
With Thibaut Metivet, Arnaud Sengers and Mourad Ismaïl we introduced diffusion redistancing schemes for computing high order geometric motion of interfaces. .

Immersed membrane under shear
With Thomas Milcent we were able to model an immersed elastic membrane with full elasticity in the level set framework.

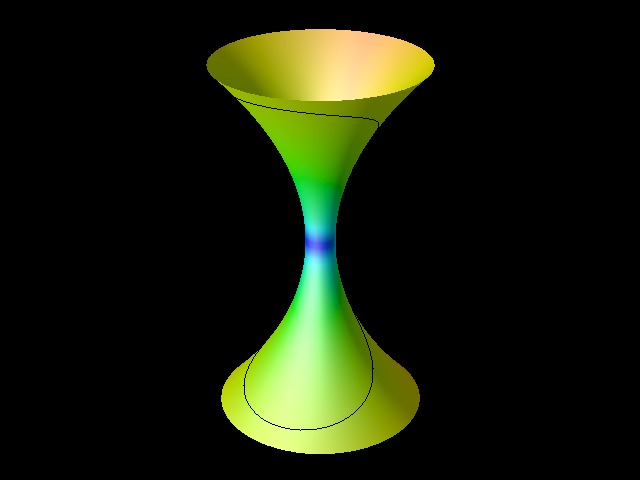
Convergence toward Willmore torus
With Thibaut Metivet, Arnaud Sengers and Mourad Ismaïl we introduced diffusion redistancing schemes for computing high order geometric motion of interfaces. .

