Limite sup et limite inf
Quand on définit une notion mathématique, le fait
qu'elle refuse de s'appliquer à certains objets la rend aussitôt
suspecte. La suite 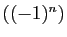 ne converge pas. Serait-ce que la notion
de limite est insuffisante ?
ne converge pas. Serait-ce que la notion
de limite est insuffisante ?
Au contraire de la limite d'une suite,
la borne supérieure et la borne inférieure d'un ensemble
existent toujours (elles peuvent être infinies).
Soit  une suite de réels. Considérons la
suite d'ensembles
une suite de réels. Considérons la
suite d'ensembles 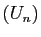 où
où 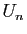 est défini par :
est défini par :
Posons alors :
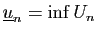
et
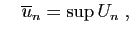
Comme les ensembles 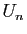 sont emboîtés (
sont emboîtés (
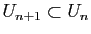 ), la
suite
), la
suite
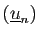 est croissante, donc elle admet une limite
(éventuellement infinie),
par le théorème 2.
Sa limite est la limite inférieure de la suite
est croissante, donc elle admet une limite
(éventuellement infinie),
par le théorème 2.
Sa limite est la limite inférieure de la suite  .
La limite supérieure est la limite de la suite
(décroissante)
.
La limite supérieure est la limite de la suite
(décroissante)
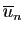 .
.
On retient de façon abrégée que
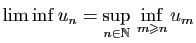
et
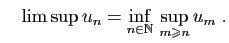
La  et la
et la 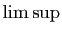 existent pour toute suite
réelle. Voici trois exemples.
existent pour toute suite
réelle. Voici trois exemples.
On peut voir la 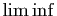 comme la plus petite limite
d'une suite extraite de la
suite
comme la plus petite limite
d'une suite extraite de la
suite  , et la
, et la 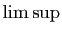 comme la plus
grande. Elles peuvent éventuellement être infinies.
On peut toujours
extraire de
comme la plus
grande. Elles peuvent éventuellement être infinies.
On peut toujours
extraire de  deux sous-suites qui
convergent vers ces deux limites. Elles fournissent une
caractérisation de la convergence : une suite
converge si et seulement si sa
deux sous-suites qui
convergent vers ces deux limites. Elles fournissent une
caractérisation de la convergence : une suite
converge si et seulement si sa 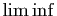 est égale à sa
est égale à sa
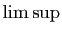 .
.
Proposition 5
Une suite de réels  converge vers
converge vers 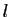 si et seulement si
si et seulement si
Démonstration : Ce résultat reste vrai si la suite tend vers
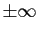 . Nous le
démontrons pour une limite finie. Rappelons la construction de
. Nous le
démontrons pour une limite finie. Rappelons la construction de
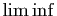 et
et 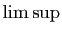 , comme limite des suites
, comme limite des suites
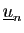 et
et
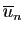 , où
, où
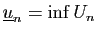
et
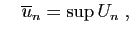
avec
Démontrons d'abord la condition
suffisante.
Par construction, la suite  est encadrée par les suites
est encadrée par les suites
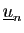 et
et
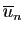 .
.
Si les deux suites
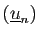 et
et
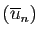 ont la
même limite, alors
ont la
même limite, alors  converge vers cette limite, par le
théorème des gendarmes (corollaire 1).
converge vers cette limite, par le
théorème des gendarmes (corollaire 1).
Réciproquement, si la suite  converge, alors pour tout
converge, alors pour tout
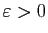 , il existe un entier
, il existe un entier  à partir duquel tous les
ensembles
à partir duquel tous les
ensembles 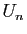 sont inclus dans l'intervalle
sont inclus dans l'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) , ce
qui implique :
, ce
qui implique :
Donc,
Cet encadrement étant vrai pour tout
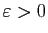 , il entraîne :
, il entraîne :

Nous avons maintenant les bons outils pour démontrer le théorème
8 :
Dans
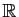 , toute suite de Cauchy converge.
Démonstration : Soit
, toute suite de Cauchy converge.
Démonstration : Soit  une suite de Cauchy dans
une suite de Cauchy dans
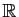 .
Commençons par montrer que
.
Commençons par montrer que  est bornée.
Fixons
est bornée.
Fixons
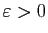 . Soit
. Soit  tel que pour tout
tel que pour tout
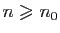 et pour tout
et pour tout
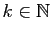 :
:
En particulier, pour tout
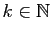 ,
,
La suite  est bornée à partir du rang
est bornée à partir du rang  , donc bornée
tout court. Donc pour tout
, donc bornée
tout court. Donc pour tout 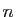 , l'ensemble
, l'ensemble
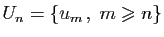 est borné et les quantités
est borné et les quantités
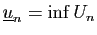 et
et
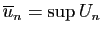 sont finies. Nous avons déjà observé
que
sont finies. Nous avons déjà observé
que
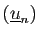 est une suite croissante et
est une suite croissante et
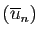 une suite décroissante, car les ensembles
une suite décroissante, car les ensembles 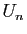 sont emboîtés. Nous allons démontrer que les suites
sont emboîtés. Nous allons démontrer que les suites
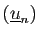 et
et
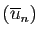 sont adjacentes,
c'est-à-dire que
sont adjacentes,
c'est-à-dire que
Fixons
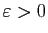 . Soit
. Soit  tel que pour tout
tel que pour tout
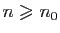 et pour tout
et pour tout
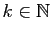 :
:
En particulier, pour tout
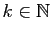 ,
,
Donc pour tout
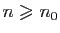 ,
,
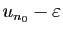 est un minorant de
l'ensemble
est un minorant de
l'ensemble 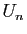 et
et
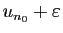 en est un majorant.
Par définition des bornes inférieure et supérieure :
en est un majorant.
Par définition des bornes inférieure et supérieure :
Donc
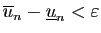 , ce que nous voulions
démontrer.
, ce que nous voulions
démontrer.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une suite de réels. Considérons la
suite d'ensembles
une suite de réels. Considérons la
suite d'ensembles ![]() où
où ![]() est défini par :
est défini par :
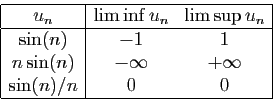
![]() converge, alors pour tout
converge, alors pour tout
![]() , il existe un entier
, il existe un entier ![]() à partir duquel tous les
ensembles
à partir duquel tous les
ensembles ![]() sont inclus dans l'intervalle
sont inclus dans l'intervalle
![]() , ce
qui implique :
, ce
qui implique :
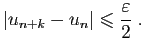
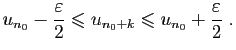
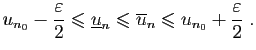
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales