Le résultat de base pour comparer deux suites est le suivant.
Démonstration : Supposons
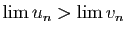 . Alors la limite de la suite
. Alors la limite de la suite
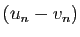 est strictement positive. Notons
est strictement positive. Notons 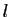 cette limite.
Pour
cette limite.
Pour 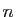 assez grand,
assez grand,
![$ u_n-v_n\in
[\frac{l}{2},\frac{3l}{2}]$](img216.gif) , donc
, donc
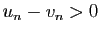 , ce qui contredit l'hypothèse.
, ce qui contredit l'hypothèse.
Observons que la conclusion reste vraie si au lieu
d'être comparables pour tout
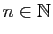 ,
,  et
et 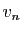 le sont «à partir d'un certain
rang». Ceci vaut d'ailleurs pour tous les résultats de cette
section.
Par contre le fait de supposer
le sont «à partir d'un certain
rang». Ceci vaut d'ailleurs pour tous les résultats de cette
section.
Par contre le fait de supposer 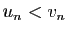 implique seulement
implique seulement
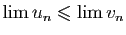 :
bien que
:
bien que 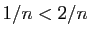 , les deux suites
, les deux suites 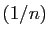 et
et 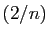 ont la même limite.
Le théorème 3 ne permet pas de démontrer
que l'une des deux suites
ont la même limite.
Le théorème 3 ne permet pas de démontrer
que l'une des deux suites  ou
ou 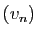 converge.
Pour cela, on utilise souvent le résultat suivant.
converge.
Pour cela, on utilise souvent le résultat suivant.
Théorème 4
Soient  et
et 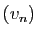 deux suites de réels telles que
deux suites de réels telles que 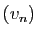 tend vers 0. Si pour tout
tend vers 0. Si pour tout
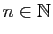 ,
,
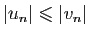 ,
alors
,
alors  tend vers 0.
tend vers 0.
Démonstration : Pour tout
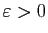 , il existe
, il existe  tel que pour
tel que pour 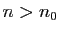 :
:
d'où le résultat.
On en déduit le corollaire suivant que l'on
trouve dans certains livres sous le nom de
«théorème des gendarmes».
Démonstration : Il suffit d'appliquer le théorème 4 aux deux suites
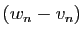 et
et 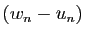 .
. 
Voici un exemple d'application.
Soit
Comme 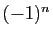 vaut
vaut 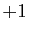 ou
ou 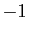 , on a l'encadrement suivant.
, on a l'encadrement suivant.
Les deux bornes de cette double inégalité
tendent vers 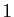 , donc
, donc
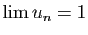 .
La comparaison vaut aussi pour les limites infinies.
.
La comparaison vaut aussi pour les limites infinies.
Théorème 5
Soient  et
et 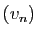 deux suites de réels telles que
pour tout
deux suites de réels telles que
pour tout
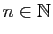 ,
,
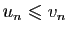 .
.
- Si
 tend vers
tend vers 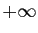 alors
alors 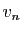 tend vers
tend vers 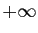 .
.
- Si
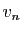 tend vers
tend vers 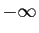 alors
alors  tend vers
tend vers 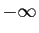 .
.
Démonstration : Pour tout 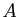 , il existe
, il existe  tel que pour
tel que pour
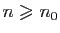 :
:
donc 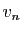 tend vers
tend vers 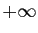 si
si  tend vers
tend vers 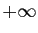 .
La démonstration de l'autre
affirmation est analogue.
.
La démonstration de l'autre
affirmation est analogue.
On dispose d'un vocabulaire adapté à la comparaison des suites.
Très souvent, on appliquera ces définitions pour une suite 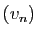 non nulle ; dans ce cas, la comparaison se lit sur le rapport
non nulle ; dans ce cas, la comparaison se lit sur le rapport
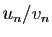 .
.
Par exemple :
L'équivalent de 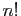 donné par la formule de Stirling est souvent
utile :
donné par la formule de Stirling est souvent
utile :
Observons que
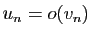 entraîne
entraîne
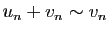 , ce qui permet
de calculer les équivalents de toutes les fonctions polynomiales de
, ce qui permet
de calculer les équivalents de toutes les fonctions polynomiales de 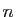 .
Les équivalents sont souvent utilisés pour le calcul de limites de
produits ou de quotients, car si
.
Les équivalents sont souvent utilisés pour le calcul de limites de
produits ou de quotients, car si
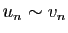 , et
, et
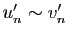 alors
alors
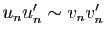 . Voici un exemple.
. Voici un exemple.
Comme
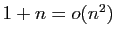 ,
,
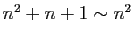 , donc
, donc
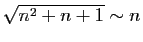 . Pour le dénominateur,
. Pour le dénominateur,
![$ \sqrt[3]{8n^3+n^2}\sim 2n$](img259.gif) , donc
, donc
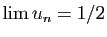 .
.
Attention, il ne faut pas
utiliser des équivalents
pour des sommes. Par exemple :
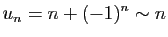
et
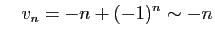
Pourtant, 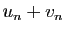 n'est pas équivalent à 0.
Voici trois résultats de comparaison de suites tendant vers
l'infini, à connaître par c
n'est pas équivalent à 0.
Voici trois résultats de comparaison de suites tendant vers
l'infini, à connaître par c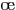 ur.
ur.
Théorème 6
Soit 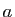 un réel strictement positif et
un réel strictement positif et 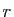 un réel strictement
supérieur à
un réel strictement
supérieur à 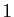 . Alors :
. Alors :
-
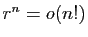 ;
;
-
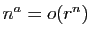 ;
;
-
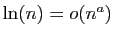 .
.
Démonstration :
- Ecrivons le rapport de
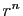 à
à 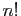 comme suit.
comme suit.
La suite
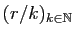 tend vers 0. Donc il existe
tend vers 0. Donc il existe 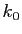 tel que
pour tout
tel que
pour tout
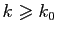 ,
,
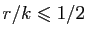 . Donc pour
. Donc pour
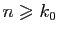 :
:
La suite
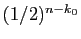 tend vers 0, d'où le résultat.
tend vers 0, d'où le résultat.
- Posons
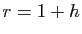 , avec
, avec 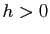 , et écrivons la formule du binôme de
Newton :
, et écrivons la formule du binôme de
Newton :
Pour tout
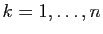 , on peut minorer
, on peut minorer 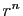 par
par
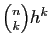 . Fixons
. Fixons
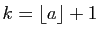 .
Pour
.
Pour 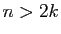 , le coefficient binomial
, le coefficient binomial
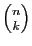 peut être
minoré comme suit.
peut être
minoré comme suit.
Donc pour tout 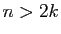 :
:
Le membre de droite tend vers 0, car par définition
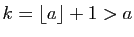 .
.
- Pour tout
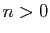 , posons :
, posons :
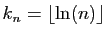
et
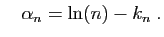
La suite 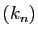 est une suite d'entiers qui tend vers l'infini, car
est une suite d'entiers qui tend vers l'infini, car
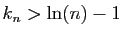 . Les
. Les 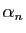 sont des réels compris entre 0 et
sont des réels compris entre 0 et
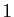 . Ecrivons :
. Ecrivons :
Dans le membre de droite, le premier terme peut-être vu comme une
suite extraite de la suite 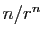 , avec
, avec
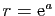 . Nous avons vu que
cette suite tend vers 0 au point 2. Donc toute suite extraite tend
aussi vers 0. Le dénominateur du second terme tend vers
l'infini. Donc
. Nous avons vu que
cette suite tend vers 0 au point 2. Donc toute suite extraite tend
aussi vers 0. Le dénominateur du second terme tend vers
l'infini. Donc
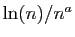 est majoré par la somme de deux suites
qui convergent vers 0. D'où le résultat.
est majoré par la somme de deux suites
qui convergent vers 0. D'où le résultat.
 Il est bon d'avoir en tête une échelle des «infiniment petits» et
des «infiniment grands», c'est-à-dire des suites qui tendent vers
0 ou vers
Il est bon d'avoir en tête une échelle des «infiniment petits» et
des «infiniment grands», c'est-à-dire des suites qui tendent vers
0 ou vers 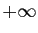 . Pour présenter ces échelles
sous forme synthétique,
nous utilisons la notation
. Pour présenter ces échelles
sous forme synthétique,
nous utilisons la notation
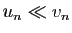 , qui est équivalente à
, qui est équivalente à
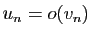 .
.
- Infiniment petits
- Infiniment grands
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() ,
, ![]() et
et ![]() le sont «à partir d'un certain
rang». Ceci vaut d'ailleurs pour tous les résultats de cette
section.
Par contre le fait de supposer
le sont «à partir d'un certain
rang». Ceci vaut d'ailleurs pour tous les résultats de cette
section.
Par contre le fait de supposer ![]() implique seulement
implique seulement
![]() :
bien que
:
bien que ![]() , les deux suites
, les deux suites ![]() et
et ![]() ont la même limite.
Le théorème 3 ne permet pas de démontrer
que l'une des deux suites
ont la même limite.
Le théorème 3 ne permet pas de démontrer
que l'une des deux suites ![]() ou
ou ![]() converge.
Pour cela, on utilise souvent le résultat suivant.
converge.
Pour cela, on utilise souvent le résultat suivant.
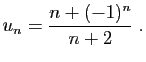
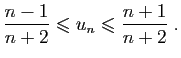
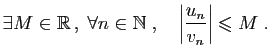
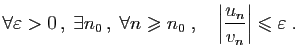
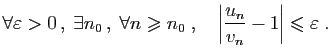
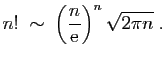
![$\displaystyle u_n = \frac{\sqrt{n^2+n+1}}{\sqrt[3]{8n^3+n^2}}\;.
$](img255.gif)
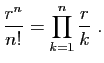
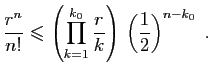
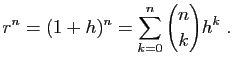
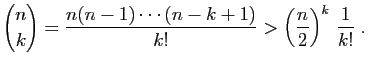
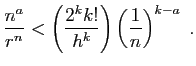
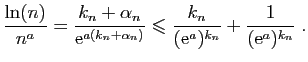
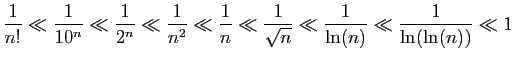
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales