Comme application de la proposition 2
(deux suites adjacentes convergent vers la même limite),
nous présentons sur deux exemples une technique
d'encadrement très efficace, la
dichotomie (action de partager
en deux).
Le premier exemple est un
résultat d'existence de point fixe.
Proposition 6
Soit 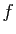 une application continue
de l'intervalle
une application continue
de l'intervalle ![$ [0,1]$](img716.gif) dans lui-même.
Alors
dans lui-même.
Alors 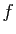 admet un point fixe :
admet un point fixe :
Démonstration : La démonstration que nous proposons est
constructive : on peut la transformer en un algorithme pour
calculer une valeur approchée du point fixe.
Posons 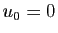 et
et 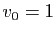 . Si
. Si
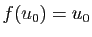 , ou si
, ou si
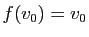 ,
inutile d'aller plus loin, on a trouvé un point fixe. Sinon, on a
forcément
,
inutile d'aller plus loin, on a trouvé un point fixe. Sinon, on a
forcément 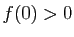 et
et 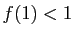 .
Examinons le point
.
Examinons le point 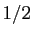 : si
: si
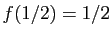 , le point fixe est
trouvé. Si
, le point fixe est
trouvé. Si
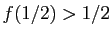 , on pose
, on pose 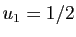 et
et 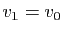 . Si
. Si
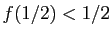 , on pose
, on pose 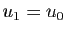 et
et 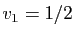 . On itère ensuite la
construction. Supposons que
. On itère ensuite la
construction. Supposons que  et
et 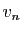 ont été construits de
sorte que
ont été construits de
sorte que
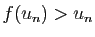 et
et
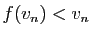 . On examine le point
. On examine le point
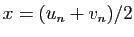 : si
: si 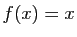 , le point fixe est
trouvé. Si
, le point fixe est
trouvé. Si 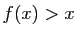 , on pose
, on pose 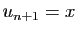 et
et
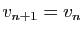 . Si
. Si
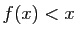 , on pose
, on pose
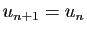 et
et 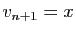 .
Plaçons nous dans le cas où la procédure se prolonge jusqu'à
l'infini (on ne trouve jamais de point fixe).
Vu la manière dont elles ont été construites, les suites
.
Plaçons nous dans le cas où la procédure se prolonge jusqu'à
l'infini (on ne trouve jamais de point fixe).
Vu la manière dont elles ont été construites, les suites  et
et 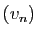 sont adjacentes :
sont adjacentes :  est croissante,
est croissante, 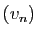 est
décroissante et
est
décroissante et
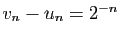 . Donc elles convergent vers la
même limite
. Donc elles convergent vers la
même limite 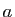 . Comme
. Comme 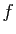 est continue les suites
est continue les suites 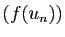 et
et
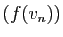 convergent vers
convergent vers 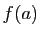 . Par construction,
. Par construction,
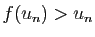 , donc
, donc
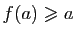 . De même,
. De même,
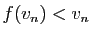 , donc
, donc
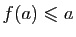 . Donc
. Donc
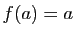 :
: 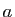 est bien un point fixe.
est bien un point fixe.
Voici un résultat beaucoup plus important, démontré également par
dichotomie :
le théorème de Bolzano-Weierstrass.
Théorème 10
De toute suite bornée, on peut extraire une sous-suite convergente.
Démonstration : Soit 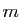 un minorant et
un minorant et 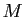 un majorant de la suite
un majorant de la suite  :
:
Posons 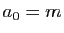 et
et 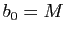 , et
, et
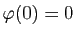 .
Divisons l'intervalle
.
Divisons l'intervalle ![$ [a_0,b_0]$](img752.gif) en deux,
et considérons les deux moitiés : l'une au moins contient une
infinité de termes de la suite
en deux,
et considérons les deux moitiés : l'une au moins contient une
infinité de termes de la suite  . Supposons que
. Supposons que
![$ [a_0,\frac{a_0+b_0}{2}]$](img753.gif) contienne une infinité de termes de la
suite. On note
contienne une infinité de termes de la
suite. On note 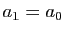 ,
,
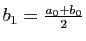 , et
, et 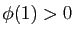 un
entier tel que
un
entier tel que
![$ u_{\phi(1)}\in [a_1,b_1]$](img757.gif) . Si la première moitié
ne contient qu'un nombre fini de termes, on la remplace par l'autre
moitié
. Si la première moitié
ne contient qu'un nombre fini de termes, on la remplace par l'autre
moitié
![$ [\frac{a_0+b_0}{2},b_0]$](img758.gif) . On itère ensuite le
procédé, de manière à construire des intervalles
emboîtés
. On itère ensuite le
procédé, de manière à construire des intervalles
emboîtés ![$ [a_k,b_k]$](img759.gif) , de longueur
, de longueur 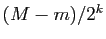 , et des valeurs
extraites
, et des valeurs
extraites
![$ u_{\phi(k)}\in [a_k,b_k]$](img761.gif) . Les suites
. Les suites 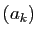 et
et 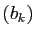 sont
adjacentes par construction, donc elles convergent vers la même
limite. Par le théorème des gendarmes (corollaire
1) la suite
sont
adjacentes par construction, donc elles convergent vers la même
limite. Par le théorème des gendarmes (corollaire
1) la suite
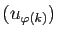 converge vers la
même limite que
converge vers la
même limite que 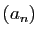 et
et 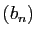 .
. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales