Dualité

D'après le théorème 9, une combinaison linéaire d'applications linéaires est encore une application linéaire. Donc l'ensemble des applications linéaires de dans est un espace vectoriel. L'espace des applications linéaires de dans $\mathbb{R}$ joue un rôle important autant en algèbre qu'en analyse : on l'appelle l'espace dual, et on le note . Une application linéaire de dans $\mathbb{R}$ s'appelle une forme linéaire. Plaçons-nous d'abord en dimension finie : est un espace vectoriel de dimension . Sauf si celle-ci est nulle, l'image d'une forme linéaire est $\mathbb{R}$ , et son rang est donc . D'après le théorème du rang (théorème 12), la dimension du noyau est . Le noyau d'une forme linéaire s'appelle un hyperplan (un plan ordinaire si est de dimension ).

Munissons d'une base, $(b_1,\ldots,b_n)$ . Parmi les formes linéaires définies sur , les applications coordonnées jouent un rôle particulier. Nous les notons $b^*_1,\ldots,b^*_n$ . Pour tout $i=1,\ldots,n$ , est l'application qui à un vecteur de associe sa -ième coordonnée dans la base $(b_1,\ldots,b_n)$ .

$\displaystyle b^*_i\;:\quad v=x_1 b_1+\cdots+x_i b_i+\cdots +x_n b_n\longmapsto b^*_i(v)=x_i\;.$

Théorème 15 La famille $(b^*_1,\ldots,b^*_n)$ est une base de .

En conséquence, l'espace vectoriel

et son dual

ont la même dimension. Démonstration : Montrons d'abord que la famille $(b^*_1,\ldots,b^*_n)$ est libre. Supposons que la forme linéaire

$\displaystyle v^*= \lambda^*_1 b^*_1+\cdots+\lambda^*_n b^*_n$

est nulle, c'est-à-dire que l'image qu'elle donne de tout vecteur est 0. En particulier l'image qu'elle donne du vecteur

est nulle. Or,

$\displaystyle b^*_i(b_i)=1$ et $\displaystyle \quad b^*_j(b_i)=0 ,\;\forall j\neq i\;.$

Donc $v^*(b_i)=\lambda^*_i=0$ . La forme

ne peut être nulle que si tous les $\lambda^*_i$ sont nuls. Montrons maintenant que la famille $(b^*_1,\ldots,b^*_n)$ est génératrice. Soit

une forme linéaire quelconque. D'après la proposition 8,

est déterminée par les images qu'elle donne aux vecteurs de la base $(b_1,\ldots,b_n)$ . Notons $\lambda^*_1,\ldots,\lambda^*_n$ ces images :

$\displaystyle \forall i=1,\ldots,n\;,\quad v^*(b_i)=\lambda^*_i\in\mathbb{R}\;.$

On vérifie facilement que

est combinaison linéaire des

$\displaystyle v^*= \lambda^*_1 b^*_1+\cdots+\lambda^*_n b^*_n\;.$

$\square$

Le mot «dual» évoque une certaine symétrie entre et : tout se passe comme si était une image miroir de . On note traditionnellement par $\langle \cdot ,\cdot\rangle$ le crochet de dualité, à savoir l'image d'un vecteur par une forme linéaire :

$\displaystyle \langle v^* , v\rangle = v^*(v)\in\mathbb{R}\;.$

Le crochet de dualité est linéaire par rapport à chacun des arguments.

$\displaystyle \langle v^* , \lambda v_1+\mu v_2\rangle$	$\displaystyle =$	$\displaystyle \lambda \langle v^, v_1\rangle +\mu \langle v^, v_2\rangle$
$\displaystyle \langle \lambda^* v^_1+\mu^ v^*_2 , v\rangle$	$\displaystyle =$	$\displaystyle \lambda^* \langle v^_1,v\rangle +\mu^ \langle v^*_2,v\rangle \;.$

Le résultat suivant illustre l'aspect miroir de la dualité.

Proposition 9 Soient et deux espaces vectoriels et une application linéaire de dans . Il existe une application linéaire unique , de vers , telle que pour tout $v\in E$ et pour tout $w^*\in F^*$ ,

$\displaystyle \langle w^* , f(v)\rangle = \langle f^*(w^*) , v \rangle \;.$

Soit $(b_1,\ldots,b_n)$ une base de , $(c_1,\ldots,c_m)$ une base de , et

$\displaystyle A=(a_{i,j}) ,\;i=1,\ldots,m , j=1,\ldots,n\;,$

la matrice de dans ces bases. Alors la matrice de dans les bases $(c^*_1,\ldots,c^*_m)$ (au départ) et $(b^*_1,\ldots,b^*_n)$ (à l'arrivée) est la transposée de la matrice , à savoir la matrice à lignes et colonnes :

$\displaystyle {^t\!A}=(a_{j,i}) ,\;j=1,\ldots,n , i=1,\ldots,m\;.$

Par exemple :

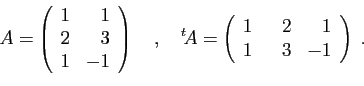
$\begin{displaymath} A= \left( \begin{array}{rr} 1&1\\ 2&3\\ 1&-1 \end{array}\r... ...{array}{rrr} 1&\hspace{3mm}2&1\\ 1&3&-1 \end{array}\right)\;. \end{displaymath}$

Démonstration : La double linéarité du crochet de dualité permet de travailler uniquement sur les images des vecteurs de bases. Soit

un indice entre

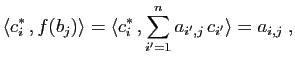
$\displaystyle \langle c^*_i , f(b_j)\rangle = \langle c^*_i , \sum_{i'=1}^na_{i',j} c_{i'}\rangle = a_{i,j}\;,$

par définition de la base duale $(c^*_1,\ldots,c^*_m)$ . Notons $(a^*_{j,i})_{j=1,\ldots,n,i=1,\ldots,m}$ la matrice de l'application

. On a de même :

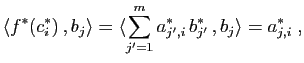
$\displaystyle \langle f^*(c^*_i) ,b_j\rangle = \langle \sum_{j'=1}^m a^*_{j',i} b^*_{j'} ,b_j\rangle = a^*_{j,i}\;,$

et donc nécessairement $a_{i,j} = a^*_{j,i}$ , car $\langle c^*_i , f(b_j)\rangle =\langle f^*(c^*_i) ,b_j\rangle$ .

La relation $\langle w^* ,f(v)\rangle = \langle f^*(w^*) ,v\rangle$ étant vérifiée pour et , elle est vraie pour tous $v\in E$ et $w^*\in F^*$ , par la double linéarité. D'où l'existence. L'application est unique car elle est déterminée par sa matrice.

$\square$

La notion de dualité prend toute sa puissance en dimension infinie pour les espaces de fonctions, quand on y ajoute une notion de continuité que nous n'expliciterons pas. Le dual d'un espace de fonctions est l'ensemble des formes linéaires continues définies sur cet espace.

Comme premier exemple, notons ${\cal C}_0([0,1])$ l'espace vectoriel des fonctions continues sur l'intervalle . Voici une forme linéaire définie sur ${\cal C}_0([0,1])$

$\displaystyle f\in {\cal C}_0([0,1]) \longmapsto \int_0^1 f(x) dx\;.$

Soit

un élément quelconque de ${\cal C}_0([0,1])$ . L'application

$\displaystyle f\in {\cal C}_0([0,1]) \longmapsto \int_0^1 f(x) g(x) dx\;,$

est encore une forme linéaire sur ${\cal C}_0([0,1])$ . Il y en a beaucoup d'autres : le dual de ${\cal C}_0([0,1])$ est l'espace des mesures de Radon sur

En dimension infinie, les duaux ont la propriété de s'emboîter à l'inverse des espaces fonctionnels dont ils sont issus. Par exemple l'espace ${\cal C}_1([0,1])$ des fonctions continues sur et dérivables sur est inclus dans ${\cal C}_0([0,1])$ . Son dual contient le dual de ${\cal C}_0([0,1])$ . Pour fabriquer un très gros espace vectoriel, qui englobe les fonctions, les mesures, et bien d'autres objets utiles, il faut prendre le dual d'un espace fonctionnel très petit. En novembre 1944, au cours de ce qu'il décrit comme «la plus belle nuit de sa vie» dans ses mémoires, Laurent Schwartz a eu l'idée de prendre le dual de l'espace des fonctions indéfiniment dérivables, nulles en dehors d'un intervalle fermé et borné : ${\cal C}_\infty^b$ . Les objets de ce dual généralisent à la fois les fonctions et les mesures : ce sont les distributions. Un des miracles des distributions est la possibilité de les dériver à volonté, par la formule «miroir» :

$\displaystyle \forall \phi\in{\cal C}_\infty^b\;,\quad \langle f , \phi'\rangle = -\langle f' , \phi\rangle \;.$

Prenons pour

la fonction de Heaviside :

$\begin{displaymath} f\;;\quad x\longmapsto \left\{ \begin{array}{l} 0\mbox{ si } x< 0\\ 1\mbox{ si } x\geqslant 0\\ \end{array}\right. \end{displaymath}$

Cette fonction s'identifie à la forme linéaire

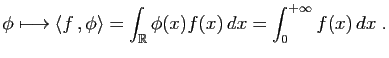
$\displaystyle \phi\longmapsto \langle f ,\phi\rangle=\int_\mathbb{R}\phi(x) f(x) dx=\int_0^{+\infty}f(x) dx\;.$

Sa dérivée au sens des distributions est la masse de Dirac en 0, à savoir la forme linéaire $\delta_0$ , définie par :

$\displaystyle \delta_0\;:\quad \phi\longmapsto \langle \delta_0 \phi\rangle=\phi(0)\;.$

Ceci n'a pas surpris les physiciens, qui depuis un quart de siècle ne se privaient pas de dériver la fonction de Heaviside (et d'autres) chaque fois qu'ils en avaient besoin...