Une application entre deux espaces vectoriels est dite linéaire si elle envoie une combinaison linéaire de vecteurs
sur la même combinaison linéaire de leurs images.
Une application linéaire 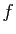 de
de  dans
dans 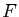 envoie nécessairement le vecteur nul de
envoie nécessairement le vecteur nul de  sur le vecteur nul de
sur le vecteur nul de
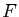 . Elle envoie l'opposé de
. Elle envoie l'opposé de 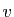 sur l'opposé de
sur l'opposé de 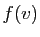 . La
proposition suivante se démontre facilement, dans le style du
théorème 2.
. La
proposition suivante se démontre facilement, dans le style du
théorème 2.
Voici quelques exemples d'applications linéaires.
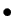
- de
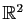 dans
dans
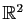 :
:
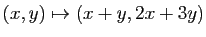
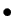
- de
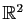 dans
dans
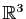 :
:
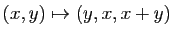
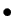
- de
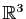 dans
dans
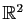 :
:
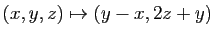
Une application linéaire respecte la structure d'espace
vectoriel : l'image d'une somme est la somme des images, l'image du
produit par un réel est le produit de l'image par le même réel.
D'une application entre deux structures algébriques (groupes, corps,
etc...) qui respecte la structure, on dit qu'elle est un morphisme. Le vocabulaire classique est le suivant.
Définition 12
Une application linéaire de  dans
dans 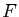 est un
est un
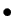
- endomorphisme si
 ,
,
- isomorphisme si elle est bijective,
- automorphisme si
 et l'application est bijective.
et l'application est bijective.
La composée de deux applications linéaires est une application
linéaire.
Démonstration : On utilise successivement la linéarité de 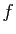 et celle de
et celle de 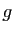 .
.

Si une application 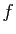 est un isomorphisme, son application
réciproque, que nous
noterons
est un isomorphisme, son application
réciproque, que nous
noterons 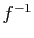 est aussi une
application linéaire.
est aussi une
application linéaire.
Théorème 8
Soit 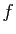 un isomorphisme de
un isomorphisme de  dans
dans 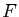 . Sa réciproque
. Sa réciproque 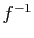 est un
isomorphisme de
est un
isomorphisme de 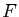 dans
dans  .
.
Démonstration : Nous devons vérifier que pour tous 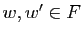 , et pour tous
, et pour tous
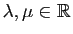 ,
,
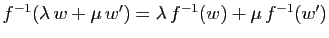 .
Puisque
.
Puisque 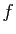 est bijective, il existe
est bijective, il existe 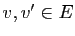 tels que
tels que 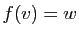 et
et
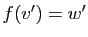 . Utilisons la linéarité de
. Utilisons la linéarité de 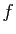 pour écrire :
pour écrire :

La composée de 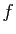 par
par 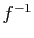 est l'application identique, ou identité, de
est l'application identique, ou identité, de  dans lui-même. C'est un automorphisme
particulier, que nous noterons
dans lui-même. C'est un automorphisme
particulier, que nous noterons 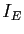 .
.
Une combinaison linéaire
d'applications linéaires est encore une application
linéaire.
Théorème 9
Soient  et
et 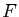 deux espaces vectoriels.
Soient
deux espaces vectoriels.
Soient 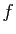 et
et 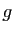 deux applications
linéaires de
deux applications
linéaires de  dans
dans 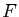 et
et
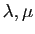 deux réels. L'application
deux réels. L'application
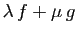 est encore une application linéaire.
est encore une application linéaire.
Démonstration : L'application
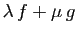 est celle qui à
est celle qui à 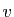 associe
associe
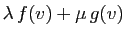 . Sa linéarité se déduit facilement
de celles de
. Sa linéarité se déduit facilement
de celles de 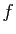 et
et 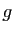 .
.
Nous terminons la section par des interprétations géométriques
d'applications
linéaires de
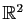 dans
dans
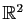 . Considérons un plan vectoriel
muni d'une base orthonormée
. Considérons un plan vectoriel
muni d'une base orthonormée
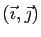 .
A tout couple de réels
.
A tout couple de réels 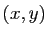 est associé le vecteur
est associé le vecteur
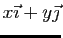 .
Une application linéaire de
.
Une application linéaire de
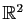 dans
lui-même est associée à une transformation géométrique du
plan, qui à un vecteur associe un autre vecteur. En voici trois
(cf. figure 1) :
dans
lui-même est associée à une transformation géométrique du
plan, qui à un vecteur associe un autre vecteur. En voici trois
(cf. figure 1) :
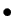
- rotation d'angle
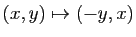
- symétrie par rapport à la première bissectrice
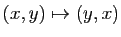
- projection sur la première bissectrice
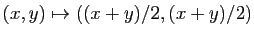
Figure 1:
Interprétations géométriques de trois applications
linéaires de
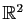 dans
dans
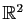 : rotation d'angle
: rotation d'angle 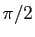 ,
symétrie par rapport à la première bissectrice, projection sur
la première bissectrice.
,
symétrie par rapport à la première bissectrice, projection sur
la première bissectrice.
|
|
Les rotations et les symétries sont des automorphismes du plan
vectoriel. Les projections sont des endomorphismes, mais elles ne sont
pas bijectives. Observons que les translations, par
exemple
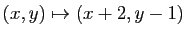 , ne sont pas linéaires. Ce sont des
bijections, mais pas des automorphismes du plan vectoriel.
, ne sont pas linéaires. Ce sont des
bijections, mais pas des automorphismes du plan vectoriel.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
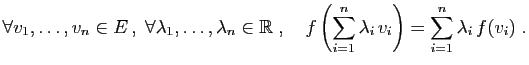
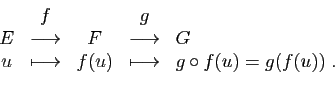
![]() est un isomorphisme, son application
réciproque, que nous
noterons
est un isomorphisme, son application
réciproque, que nous
noterons ![]() est aussi une
application linéaire.
est aussi une
application linéaire.
![]() par
par ![]() est l'application identique, ou identité, de
est l'application identique, ou identité, de ![]() dans lui-même. C'est un automorphisme
particulier, que nous noterons
dans lui-même. C'est un automorphisme
particulier, que nous noterons ![]() .
.
![]() dans
dans
![]() . Considérons un plan vectoriel
muni d'une base orthonormée
. Considérons un plan vectoriel
muni d'une base orthonormée
![]() .
A tout couple de réels
.
A tout couple de réels ![]() est associé le vecteur
est associé le vecteur
![]() .
Une application linéaire de
.
Une application linéaire de
![]() dans
lui-même est associée à une transformation géométrique du
plan, qui à un vecteur associe un autre vecteur. En voici trois
(cf. figure 1) :
dans
lui-même est associée à une transformation géométrique du
plan, qui à un vecteur associe un autre vecteur. En voici trois
(cf. figure 1) :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales