Qu'une application linéaire respecte les combinaisons linéaires
entraîne qu'elle respecte aussi les sous-espaces vectoriels, au
sens suivant.
L'ensemble des images par une application linéaire des éléments
d'un espace vectoriel est un sous-espace vectoriel de l'espace
d'arrivée (point 1). L'ensemble des éléments de l'espace
de départ dont l'image par une application linéaire est dans un
sous-espace de l'espace d'arrivée, est un sous-espace de l'espace de
départ (point 2).
Attention à la notation 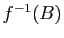 : elle a un sens même si
l'application
: elle a un sens même si
l'application  n'est pas bijective et donc si
l'application réciproque
n'est pas bijective et donc si
l'application réciproque 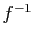 n'existe pas.
Démonstration : Pour montrer qu'un sous-ensemble est un sous-espace vectoriel, il
suffit de vérifier qu'il est non vide, et
que toute combinaison linéaire de deux de ses
vecteurs reste dans l'ensemble (théorème 2).
Rappelons que tout sous-espace vectoriel contient au moins le vecteur
nul, et que si
n'existe pas.
Démonstration : Pour montrer qu'un sous-ensemble est un sous-espace vectoriel, il
suffit de vérifier qu'il est non vide, et
que toute combinaison linéaire de deux de ses
vecteurs reste dans l'ensemble (théorème 2).
Rappelons que tout sous-espace vectoriel contient au moins le vecteur
nul, et que si  est linéaire alors
est linéaire alors 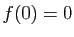 . Donc le vecteur nul
de
. Donc le vecteur nul
de  appartient à
appartient à 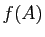 et celui de
et celui de  appartient à
appartient à
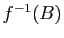 . Les deux ensembles
. Les deux ensembles 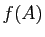 et
et 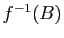 sont donc non
vides.
sont donc non
vides.
- Deux vecteurs quelconques de
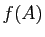 s'écrivent
s'écrivent
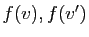 , où
, où
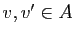 . Etant donnés deux réels
. Etant donnés deux réels 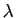 et
et 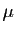 ,
,
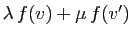 est l'image par
est l'image par  de
de
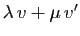 qui est
un vecteur de
qui est
un vecteur de 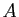 .
.
- Si
 et
et 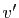 sont tels que
sont tels que 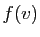 et
et 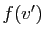 appartiennent à
appartiennent à 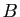 ,
alors
,
alors
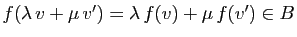 . Donc
. Donc
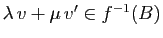 .
.

Parmi les cas particuliers du théorème 10,
l'image et
le noyau jouent un rôle important.
La notation Ker vient de l'allemand, où noyau se dit «Kern».
Considérons par exemple l'application  de
de
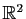 dans
dans
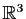 définie par :
définie par :
Son image est la droite vectorielle de
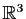 engendrée par le
vecteur
engendrée par le
vecteur 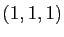 . Son noyau est l'ensemble des vecteurs
. Son noyau est l'ensemble des vecteurs 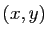 de
de
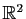 tels que
tels que 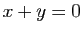 : c'est la droite vectorielle de
: c'est la droite vectorielle de
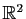 engendrée par le vecteur
engendrée par le vecteur 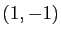 .
.
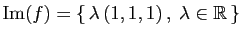
et
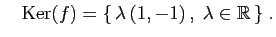
Proposition 7
Soient  et
et  deux espaces vectoriels et
deux espaces vectoriels et  une application
linéaire de
une application
linéaire de  dans
dans  . L'application
. L'application  est :
est :
- surjective si et seulement si
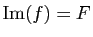 ,
,
- injective si et seulement si
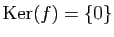 .
.
Démonstration : La caractérisation de la surjectivité est une simple traduction
des définitions. Celle de l'injectivité utilise la linéarité.
Soient  et
et 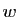 deux éléments de
deux éléments de  .
.
Par définition,  est injective si et seulement si
est injective si et seulement si
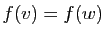 implique
implique 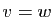 , donc si et seulement si
, donc si et seulement si
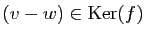 implique
implique 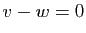 , d'où le résultat.
, d'où le résultat.
Le rang d'une application linéaire est la dimension de son
image.
Supposons que  soit de dimension
soit de dimension  et choisissons une base
et choisissons une base
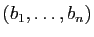 .
L'image par
.
L'image par  de tout vecteur de
de tout vecteur de  est
une combinaison linéaire des vecteurs
est
une combinaison linéaire des vecteurs
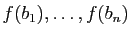 . Donc
. Donc
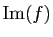 est le sous-espace vectoriel de
est le sous-espace vectoriel de  engendré par
engendré par
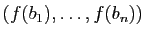 . Le rang de
. Le rang de  est la dimension de ce
sous-espace ; c'est donc le rang de la famille de vecteurs
est la dimension de ce
sous-espace ; c'est donc le rang de la famille de vecteurs
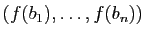 (cf. définition
10). Observons que le rang est inférieur ou
égal aux deux dimensions des espaces vectoriels de départ et
d'arrivée.
(cf. définition
10). Observons que le rang est inférieur ou
égal aux deux dimensions des espaces vectoriels de départ et
d'arrivée.
Théorème 11
Soit  et
et  deux espaces vectoriels de dimension finie.
Soit
deux espaces vectoriels de dimension finie.
Soit  une application linéaire de
une application linéaire de  dans
dans  .
L'application
.
L'application  est :
est :
- surjective si et seulement si l'image de toute famille génératrice
dans
 est une famille génératrice dans
est une famille génératrice dans  ,
,
- injective si et seulement si l'image de toute famille libre dans
 est une famille libre dans
est une famille libre dans  ,
,
- bijective si et seulement si l'image de toute base de
 est une base de
est une base de  .
.
Démonstration : Démontrons d'abord que si  est surjective alors l'image d'une
famille génératrice dans
est surjective alors l'image d'une
famille génératrice dans  est génératrice dans
est génératrice dans  .
Soit
.
Soit
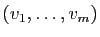 une famille génératrice dans
une famille génératrice dans  .
Pour tout
élément
.
Pour tout
élément  de
de  , il existe
, il existe 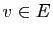 tel que
tel que
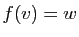 . Le vecteur
. Le vecteur  s'écrit :
s'écrit :
Donc :
Tout vecteur 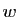 de
de  est combinaison linéaire de la famille
est combinaison linéaire de la famille
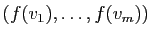 , qui est donc génératrice.
, qui est donc génératrice.
Voici la réciproque. Si
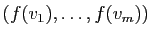 est
génératrice, alors un vecteur
est
génératrice, alors un vecteur 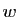 de
de  quelconque s'écrit
quelconque s'écrit
Donc 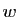 est l'image par
est l'image par  d'un vecteur de
d'un vecteur de  :
:  est bien
surjective.
Démontrons maintenant que si
est bien
surjective.
Démontrons maintenant que si  est injective alors l'image d'une
famille libre dans
est injective alors l'image d'une
famille libre dans  est une famille libre dans
est une famille libre dans  .
Soit
.
Soit
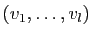 une famille libre dans
une famille libre dans  .
Supposons que
.
Supposons que
Par la linéarité de  ,
,
Si  est injective, alors le seul vecteur d'image nulle est le
vecteur nul, donc
est injective, alors le seul vecteur d'image nulle est le
vecteur nul, donc
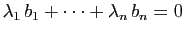 . Mais
. Mais
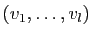 est une famille libre. Donc
est une famille libre. Donc
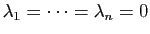 .
.
Montrons la réciproque. Si l'image de toute famille libre
est une famille libre, alors l'image d'un vecteur non nul est un
vecteur non nul. Donc
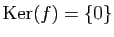 et
et  est injective, par
la proposition 7.
Pour terminer la démonstration, il suffit d'observer qu'une
application est bijective si et seulement si elle est à la fois
injective et surjective ; d'autre part une famille est une base si et
seulement si elle est à la fois libre et génératrice. Le point
3 du théorème est donc conséquence des deux précédents.
est injective, par
la proposition 7.
Pour terminer la démonstration, il suffit d'observer qu'une
application est bijective si et seulement si elle est à la fois
injective et surjective ; d'autre part une famille est une base si et
seulement si elle est à la fois libre et génératrice. Le point
3 du théorème est donc conséquence des deux précédents.
La conjonction des théorèmes 11 et
4 implique les relations suivantes entre les
dimensions des espaces de départ et d'arrivée.
Corollaire 2
Soient  et
et  deux espaces vectoriels de dimension finie et
deux espaces vectoriels de dimension finie et
 une application linéaire de
une application linéaire de  dans
dans  .
.
- Si
 est surjective alors
est surjective alors
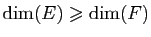 .
.
- Si
 est injective alors
est injective alors
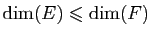 .
.
- Si
 est bijective alors
est bijective alors
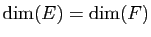 .
.
La dimension est donc une forte contrainte sur la nature des
applications linéaires. On peut aussi voir cette contrainte comme suit.
Corollaire 3
Soient  et
et  deux espaces vectoriels de même dimension. Une
application linéaire de
deux espaces vectoriels de même dimension. Une
application linéaire de  dans
dans  est bijective si et seulement
si elle est injective ou surjective.
est bijective si et seulement
si elle est injective ou surjective.
Il ne peut exister un isomorphisme entre
deux espaces vectoriels que s'ils ont la même
dimension. Réciproquement, si deux espaces ont la même dimension,
on peut toujours construire un isomorphisme entre eux, en envoyant une
base de l'un sur une base de l'autre. En particulier, tous les espaces
vectoriels de dimension  sont isomorphes à
sont isomorphes à
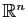 . Si
. Si  est
de dimension
est
de dimension  , avec une base
, avec une base
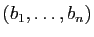 , tous les
vecteurs de
, tous les
vecteurs de  ont une décomposition unique
ont une décomposition unique
où les 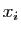 sont les coordonnées de
sont les coordonnées de  (théorème 5). L'application de
(théorème 5). L'application de  dans
dans
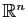 qui à
qui à  associe le
associe le  -uplet de ses coordonnées
-uplet de ses coordonnées
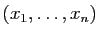 est un isomorphisme de
est un isomorphisme de  dans
dans
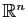 .
La somme des dimensions de l'image et du noyau
est la dimension de l'espace de départ : le
théorème 12 ci-dessous, est le
théorème du rang.
.
La somme des dimensions de l'image et du noyau
est la dimension de l'espace de départ : le
théorème 12 ci-dessous, est le
théorème du rang.
Démonstration : Soient 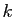 et
et 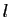 les dimensions respectives de
les dimensions respectives de
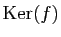 et
Im
et
Im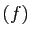 . Soit
. Soit
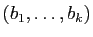 une base de
une base de
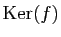 et
et
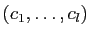 une base de
Im
une base de
Im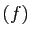 . Pour
. Pour
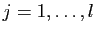 ,
soit
,
soit 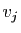 un vecteur de
un vecteur de  tel que
tel que
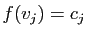 . Nous allons
démontrer que
. Nous allons
démontrer que
est une base de  , ce qui entraîne que
, ce qui entraîne que
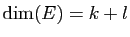 .
Montrons d'abord que c'est une famille libre.
Soient
.
Montrons d'abord que c'est une famille libre.
Soient
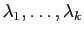 et
et
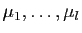 ,
, 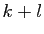 réels. Posons
réels. Posons
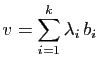
et
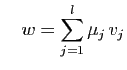
Puisque
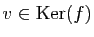 ,
l'image par
,
l'image par  du vecteur
du vecteur 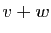 est
est
Si 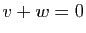 , alors
, alors 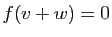 , ce qui entraîne la nullité des
, ce qui entraîne la nullité des
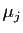 , car
, car
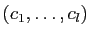 est une famille libre. Alors
est une famille libre. Alors
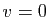 , ce qui entraîne la nullité des
, ce qui entraîne la nullité des
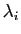 , car
, car
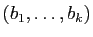 est une famille libre.
Donc
est une famille libre.
Donc 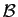 est une famille libre.
est une famille libre.
Il reste à montrer que 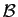 est une famille génératrice.
Soit
est une famille génératrice.
Soit  un vecteur de
un vecteur de  . Comme le vecteur
. Comme le vecteur 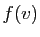 appartient à
appartient à
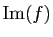 , il est combinaison linéaire de
, il est combinaison linéaire de
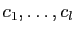 :
:
Donc :
Ceci entraîne :
donc
Donc il existe
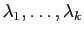 tels que
tels que
soit

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
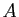 un sous-espace vectoriel de
un sous-espace vectoriel de  . Alors
est un sous-espace vectoriel de
. Alors
est un sous-espace vectoriel de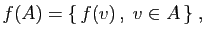
 .
.
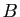 un sous-espace vectoriel de
un sous-espace vectoriel de  . Alors
est un sous-espace vectoriel de
. Alors
est un sous-espace vectoriel de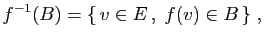
 .
.
![]() est
génératrice, alors un vecteur
est
génératrice, alors un vecteur ![]() de
de ![]() quelconque s'écrit
quelconque s'écrit
![]() et
et ![]() est injective, par
la proposition 7.
Pour terminer la démonstration, il suffit d'observer qu'une
application est bijective si et seulement si elle est à la fois
injective et surjective ; d'autre part une famille est une base si et
seulement si elle est à la fois libre et génératrice. Le point
3 du théorème est donc conséquence des deux précédents.
est injective, par
la proposition 7.
Pour terminer la démonstration, il suffit d'observer qu'une
application est bijective si et seulement si elle est à la fois
injective et surjective ; d'autre part une famille est une base si et
seulement si elle est à la fois libre et génératrice. Le point
3 du théorème est donc conséquence des deux précédents.![]()
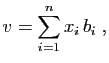
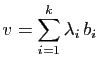 et
et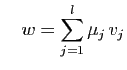
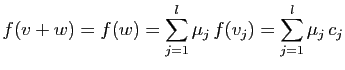
![]() est une famille génératrice.
Soit
est une famille génératrice.
Soit ![]() un vecteur de
un vecteur de ![]() . Comme le vecteur
. Comme le vecteur ![]() appartient à
appartient à
![]() , il est combinaison linéaire de
, il est combinaison linéaire de
![]() :
:
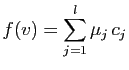
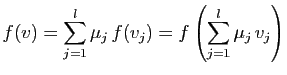
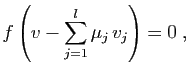
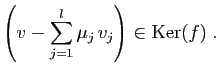
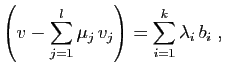
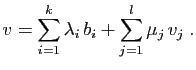
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales