La tangente au graphe d'une fonction en un point est une droite
passant par ce point, dont la pente est la dérivée. Pour une
application dérivable en 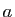 , on
peut écrire :
, on
peut écrire :
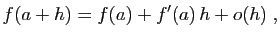 |
(3) |
où 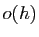 désigne une fonction telle que
désigne une fonction telle que  tend vers 0
quand
tend vers 0
quand 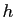 tend vers 0. Imaginons que l'on souhaite approcher
tend vers 0. Imaginons que l'on souhaite approcher
 au voisinage de
au voisinage de 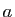 (pour une valeur de
(pour une valeur de 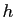 petite), sans savoir
calculer
petite), sans savoir
calculer 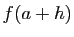 . On peut remplacer
. On peut remplacer
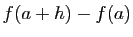 par
par 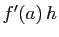 , et
l'erreur commise est négligeable devant
, et
l'erreur commise est négligeable devant 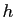 .
Dans (3), une application
linéaire de
.
Dans (3), une application
linéaire de
 dans
dans
 apparaît : l'application
apparaît : l'application
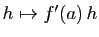 .
Ceci se généralise à des applications de
.
Ceci se généralise à des applications de
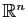 dans
dans
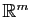 ,
avec
,
avec  et
et  quelconques. L'application
quelconques. L'application
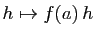 devient une application linéaire de
devient une application linéaire de
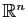 dans
dans
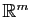 : l'application linéaire tangente.
Pour ne pas compliquer les notations, nous prendrons l'exemple
d'une application de
: l'application linéaire tangente.
Pour ne pas compliquer les notations, nous prendrons l'exemple
d'une application de
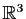 dans
dans
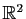
Ce pourrait être par exemple l'application qui aux trois dimensions
d'un parallélépipède associe sa surface et son volume.
Les applications  et
et 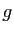 , de
, de
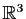 dans
dans
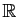 , sont les applications coordonnées. Si on fixe un point
, sont les applications coordonnées. Si on fixe un point 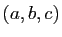 dans
l'espace de départ, on définit
dans
l'espace de départ, on définit 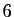 applications partielles.
applications partielles.
Nous commençons par une application  , de
, de
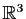 dans
dans
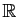 .
Si les
applications partielles sont dérivables, leurs dérivées
s'appellent les dérivées partielles en
.
Si les
applications partielles sont dérivables, leurs dérivées
s'appellent les dérivées partielles en 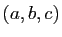 .
.
Pour calculer la dérivée partielle de  par rapport à
par rapport à 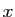 , il suffit
de dériver en
, il suffit
de dériver en 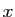 l'expression de
l'expression de  , en traitant les autres
variables comme des constantes paramétriques.
, en traitant les autres
variables comme des constantes paramétriques.
Supposons par exemple que  soit l'application qui à
soit l'application qui à 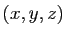 associe la surface du parallélépipède dont les longueurs
d'arêtes sont
associe la surface du parallélépipède dont les longueurs
d'arêtes sont 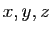 .
.
Voici ses trois dérivées partielles.
Si elles sont continues, les dérivées partielles permettent
d'approcher la fonction par une application linéaire au voisinage
d'un point. Le résultat qui suit est l'analogue pour les fonctions
de plusieurs variables du théorème des accroissements finis.
Théorème 14
Soit,
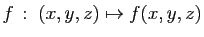 une application continûment
différentiable de
une application continûment
différentiable de
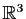 dans
dans
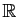 et
et 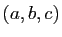 un point de
un point de
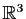 . Notons
. Notons 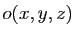 la fonction
définie par :
la fonction
définie par :
Alors :
Ce théorème dit que les variations de la fonction  autour du
point
autour du
point 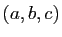 peuvent être approchées par une application
linéaire, la différentielle
de
peuvent être approchées par une application
linéaire, la différentielle
de  .
.
En physique, on interprète 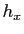 ,
, 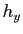 et
et 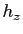 comme des petites
variations des variables
comme des petites
variations des variables 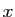 ,
, 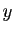 , et
, et 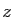 , et on les note plutôt
, et on les note plutôt
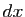 ,
, 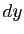 et
et 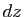 . Si on note
. Si on note 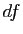 la différentielle de
la différentielle de  , ceci
justifie l'écriture abrégée suivante.
, ceci
justifie l'écriture abrégée suivante.
La différentielle est plus facile à visualiser en dimension
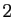 . Pour une fonction de deux variables, le théorème
14 donne une approximation de
. Pour une fonction de deux variables, le théorème
14 donne une approximation de 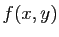 sous la forme :
sous la forme :
La surface d'équation
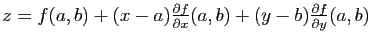 est celle du plan tangent
à la surface
est celle du plan tangent
à la surface 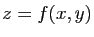 au point
au point 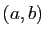 (cf.
figure 3). Pour rappeler cette
interprétation géométrique, la différentielle de
(cf.
figure 3). Pour rappeler cette
interprétation géométrique, la différentielle de  au point
au point
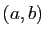 porte aussi le nom d'application linéaire tangente.
porte aussi le nom d'application linéaire tangente.
Figure 3:
Plan tangent à une surface en un point.
|
|
Une application de
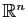 dans
dans
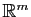 est continûment
différentiable si ses
est continûment
différentiable si ses  applications coordonnées le sont.
On peut donc lui appliquer,
coordonnée par coordonnée, le théorème
14. La différentielle en un point de
applications coordonnées le sont.
On peut donc lui appliquer,
coordonnée par coordonnée, le théorème
14. La différentielle en un point de
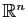 est une application linéaire de
est une application linéaire de
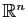 dans
dans
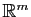 . Sa
matrice est la matrice jacobienne. Ici encore nous donnons la
définition en dimension réduite pour des raisons de clarté.
. Sa
matrice est la matrice jacobienne. Ici encore nous donnons la
définition en dimension réduite pour des raisons de clarté.
Voici la matrice
jacobienne au point 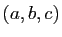 pour la surface et le volume
d'un parallélépipède en fonction de ses trois dimensions.
pour la surface et le volume
d'un parallélépipède en fonction de ses trois dimensions.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() , on
peut écrire :
, on
peut écrire :
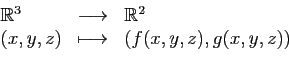
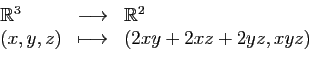
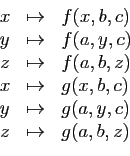
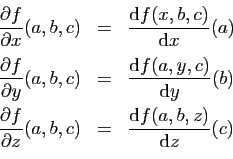
![]() soit l'application qui à
soit l'application qui à ![]() associe la surface du parallélépipède dont les longueurs
d'arêtes sont
associe la surface du parallélépipède dont les longueurs
d'arêtes sont ![]() .
.
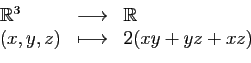
![\begin{displaymath}
\begin{array}{lcl}
\displaystyle{\frac{\partial f}{\partial ...
...partial z}(a,b,c)}&=&
\displaystyle{2(a+b)}\ [2ex]
\end{array}\end{displaymath}](img663.gif)
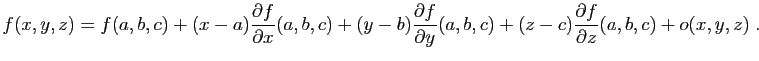
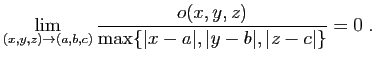
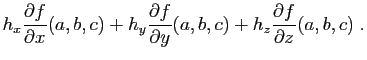
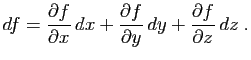
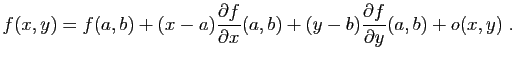
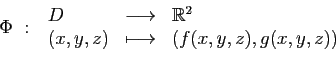
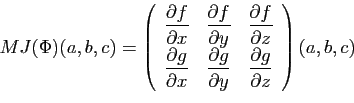
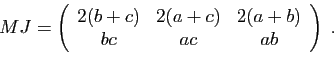
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales