Les espaces vectoriels considérés
sont tous de dimension finie
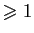 . Observons d'abord
qu'une application linéaire est déterminée
par l'image qu'elle donne d'une base de l'espace
de départ.
. Observons d'abord
qu'une application linéaire est déterminée
par l'image qu'elle donne d'une base de l'espace
de départ.
Proposition 8
Soient  et
et  deux espaces vectoriels de dimension finie.
deux espaces vectoriels de dimension finie.
Soit
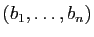 une base de
une base de  . Soit
. Soit
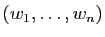 un
un
 -uplet de vecteurs de
-uplet de vecteurs de  . Il existe une application linéaire
unique
. Il existe une application linéaire
unique  telle que pour tout
telle que pour tout
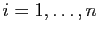 ,
,
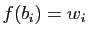 .
.
Démonstration : Tout vecteur  de
de  s'écrit de façon unique sous la forme
s'écrit de façon unique sous la forme
où les 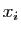 sont les coordonnées de
sont les coordonnées de  dans
la base
dans
la base
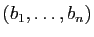 . Puisque
. Puisque  doit être linéaire,
l'image de
doit être linéaire,
l'image de  ne peut être que
ne peut être que

Si on choisit une base dans l'espace
d'arrivée, alors les images des vecteurs de la base de départ ont
des coordonnées dans cette base. S'il y a  vecteurs de base au
départ et
vecteurs de base au
départ et  à l'arrivée, l'application linéaire est
déterminée par
à l'arrivée, l'application linéaire est
déterminée par 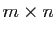 réels :
réels :  coordonnées pour chacun
des
coordonnées pour chacun
des  vecteurs de base. Une matrice est la représentation sous
forme de tableau de ces
vecteurs de base. Une matrice est la représentation sous
forme de tableau de ces 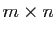 réels.
Notons
réels.
Notons
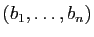 une base de l'espace de départ, et
une base de l'espace de départ, et
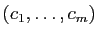 une base de l'espace d'arrivée.
Soit
une base de l'espace d'arrivée.
Soit 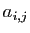 la
la 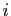 -ième
coordonnée de
-ième
coordonnée de 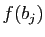 :
:
Les coordonnées des vecteurs images
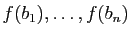 sont
conventionnellement notées en colonnes. L'indice
sont
conventionnellement notées en colonnes. L'indice 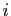 (des vecteurs de
la base d'arrivée) est l'indice de
ligne, l'indice
(des vecteurs de
la base d'arrivée) est l'indice de
ligne, l'indice 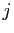 (des vecteurs de la base de départ) est l'indice
de colonne.
(des vecteurs de la base de départ) est l'indice
de colonne.
Le plus souvent, on se ramènera au cas où l'espace de départ est
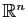 et l'espace d'arrivée
et l'espace d'arrivée
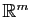 , les deux étant munis de
leurs bases canoniques. Comme premier exemple, considérons
l'application de
, les deux étant munis de
leurs bases canoniques. Comme premier exemple, considérons
l'application de
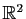 dans
dans
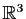 :
:
La base canonique de
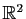 est
est
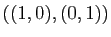 . L'image de ces
deux vecteurs est
. L'image de ces
deux vecteurs est
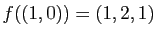
et
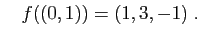
La matrice de  est donc la suivante (attention à l'écriture des
vecteurs de l'espace d'arrivée en colonnes).
est donc la suivante (attention à l'écriture des
vecteurs de l'espace d'arrivée en colonnes).
Munissons maintenant
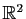 de la base
de la base
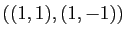 au
départ, et
au
départ, et
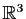 de la base
de la base
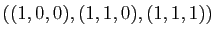 à
l'arrivée. Les images des vecteurs de la base de départ sont
à
l'arrivée. Les images des vecteurs de la base de départ sont
D'où la matrice,
Quand l'espace d'arrivée et l'espace de départ sont les mêmes
(l'application est un endomorphisme), on choisit la même base au
départ et à l'arrivée. La matrice d'un endomorphisme a autant de
lignes que de colonnes : on dit qu'elle est carrée.
Voici les matrices de trois endomorphismes de
 , dans la base
canonique.
, dans la base
canonique.
- Rotation d'angle
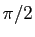 :
:
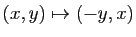
- Symétrie par rapport à la première bissectrice :
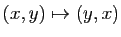
- Projection sur la première bissectrice :
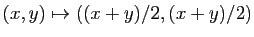
Dans un espace de dimension  , la matrice de
l'application identique est la matrice carrée
, la matrice de
l'application identique est la matrice carrée 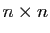 qui a des
qui a des
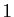 sur la diagonale (termes d'indices
sur la diagonale (termes d'indices 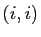 ) et des 0 en dehors
(termes d'indices
) et des 0 en dehors
(termes d'indices 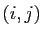 avec
avec 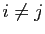 ). On
l'appelle matrice identité d'ordre
). On
l'appelle matrice identité d'ordre  et on la note
et on la note 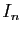 .
.
La représentation matricielle présente l'avantage d'automatiser de
nombreux calculs. Nous consacrerons le chapitre suivant au
calcul matriciel. Pour l'instant nous allons voir comment la
matrice d'une application linéaire permet de calculer l'image d'un
vecteur dont on se donne les coordonnées dans la base de départ.
Reprenons la situation générale :
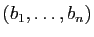 est
une base de l'espace de départ, et
est
une base de l'espace de départ, et
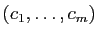 une base de l'espace d'arrivée.
Le coefficient d'indice
une base de l'espace d'arrivée.
Le coefficient d'indice 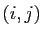 de la matrice de
de la matrice de  , noté
, noté
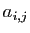 , est la
, est la 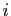 -ième
coordonnée de
-ième
coordonnée de 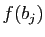 :
:
Considérons maintenant un vecteur  de l'espace de départ, dont
les coordonnées dans la base
de l'espace de départ, dont
les coordonnées dans la base
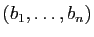 sont
sont
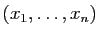 .
.
L'image de  par
par  est :
est :
Donc le vecteur 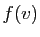 se décompose dans la base
se décompose dans la base
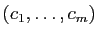 en
en
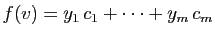 , avec :
, avec :
On dit que le vecteur
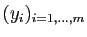 est le produit de
la matrice
est le produit de
la matrice 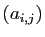 par le vecteur
par le vecteur
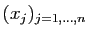 . Observez que ce produit n'a de sens que
si le nombre de coordonnées du vecteur est égal au nombre de
colonnes de la matrice.
Il est commode, pour calculer le produit d'une matrice par un vecteur,
de représenter les
. Observez que ce produit n'a de sens que
si le nombre de coordonnées du vecteur est égal au nombre de
colonnes de la matrice.
Il est commode, pour calculer le produit d'une matrice par un vecteur,
de représenter les
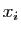 en colonne, au-dessus et à droite de la matrice
en colonne, au-dessus et à droite de la matrice
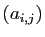 (voir figure 2).
(voir figure 2).
Figure 2:
Comment présenter le produit d'une
matrice par un vecteur colonne.
|
|
Reprenons l'exemple de
l'application de
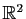 dans
dans
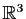 :
:
Les bases respectives de
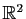 et
et
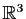 étant les bases
canoniques, la matrice de
étant les bases
canoniques, la matrice de  est :
est :
Pour vérifier la cohérence de la notation matricielle, calculons
le produit de cette matrice par un vecteur de
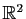 quelconque
quelconque 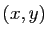 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
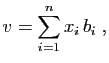
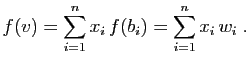
![]() vecteurs de base au
départ et
vecteurs de base au
départ et ![]() à l'arrivée, l'application linéaire est
déterminée par
à l'arrivée, l'application linéaire est
déterminée par ![]() réels :
réels : ![]() coordonnées pour chacun
des
coordonnées pour chacun
des ![]() vecteurs de base. Une matrice est la représentation sous
forme de tableau de ces
vecteurs de base. Une matrice est la représentation sous
forme de tableau de ces ![]() réels.
Notons
réels.
Notons
![]() une base de l'espace de départ, et
une base de l'espace de départ, et
![]() une base de l'espace d'arrivée.
Soit
une base de l'espace d'arrivée.
Soit ![]() la
la ![]() -ième
coordonnée de
-ième
coordonnée de ![]() :
:
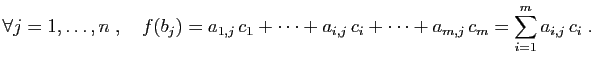
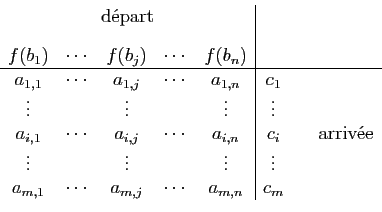
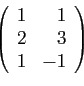
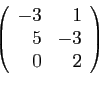
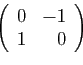
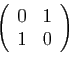
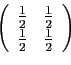

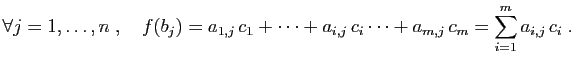
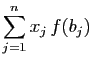
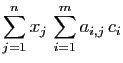
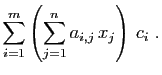
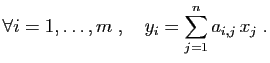
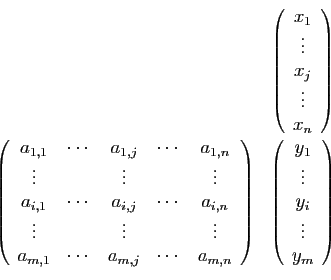
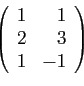
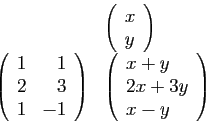
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales