Section : Compléments
Avant : Dualité

Codes de Hamming

Le plus petit corps de nombres, celui des entiers modulo $ 2$, ne contient que 0 et $ 1$. On le note $ \mathbb{Z}/2\mathbb{Z}$. Sur l'ensemble des $ n$-uplets de 0 ou de $ 1$, les opérations de $ \mathbb{Z}/2\mathbb{Z}$ agissent composante par composante. Par exemple pour $ n=4$ :

$\displaystyle (0,1,0,1)+(1,0,0,1)=(1,1,0,0)\;. $

Cet ensemble, noté $ (\mathbb{Z}/2\mathbb{Z})^n$, est un espace vectoriel sur $ \mathbb{Z}/2\mathbb{Z}$, tout comme $ \mathbb{R}^n$ est un espace vectoriel sur $ \mathbb{R}$. Deux éléments de $ (\mathbb{Z}/2\mathbb{Z})^n$ qui diffèrent en une seule coordonnée sont dits voisins. Si on met une arête entre deux $ n$-uplets voisins, on obtient un graphe, que l'on appelle l'hypercube de dimension $ n$. Pourquoi hypercube ? La figure 4 devrait vous convaincre.
Figure 4: Cube en dimension $ 3$. Chaque arête joint deux triplets qui diffèrent par une seule coordonnée.
\includegraphics[width=4cm,height=4cm]{hyper3}
L'espace vectoriel $ (\mathbb{Z}/2\mathbb{Z})^n$ est-il une fantaisie de mathématicien ? Pas du tout ! Les ordinateurs ne connaissent que les 0 et les $ 1$ (les bits), rangés en mémoire par $ n$-uplets, avec $ n=8$ (les octets ou bytes), $ n=16$, $ n=32$, $ n=64$, ...  Ils peuvent représenter n'importe quel ensemble fini, pourvu que l'on ait choisi au préalable une application injective de cet ensemble dans $ (\mathbb{Z}/2\mathbb{Z})^n$ pour un certain $ n$. Cette application s'appelle un code. Le plus connu est le code ASCII standard qui associe $ 64$ caractères (chiffres, lettres, $, %, $ /$, ...) aux éléments de $ (\mathbb{Z}/2\mathbb{Z})^6$. Les transmissions entre ordinateurs, que ce soit par câble, par ondes radio ou infra-rouges, sont des échanges de signaux composés de paquets de 0 et de $ 1$, qui ont été codés par l'émetteur et seront décodés par le récepteur. Mais si dans un paquet une erreur est commise (un 0 est changé en $ 1$ ou le contraire), alors le paquet entier, et peut-être tout le message, seront perdus. A moins que l'on utilise un code correcteur d'erreurs.

Un code est «correcteur d'erreurs»  si parmi les voisins dans l'hypercube d'un élément codé, on ne trouve jamais ni un autre élément codé, ni l'un de ses voisins. De cette façon, si un $ n$-uplet est reçu, soit il a été transmis sans erreur et il figure dans le code, soit une erreur a été commise, et elle sera corrigée en remplaçant le $ n$-uplet reçu par celui de ses voisins qui figure dans le code. Cela ne fonctionne plus si deux erreurs ou plus ont été commises, mais on peut généraliser : il existe des codes capables de corriger plusieurs erreurs.

Contentons nous pour l'instant de comprendre le problème en dimension $ 4$ (cf. figure 5). Supposons que $ (0,0,0,0)$ code un objet, alors aucun de ses $ 4$ voisins ne peut être codant ; mais si un de ces voisins est reçu, il faut pouvoir le relier à $ (0,0,0,0)$ sans ambiguïté. Donc les voisins des voisins de 0 ne peuvent pas non plus coder. Il reste $ 5$ vecteurs codants possibles, $ (0,1,1,1)$, $ (1,0,1,1)$, $ (1,1,0,1)$, $ (1,1,1,0)$ et $ (1,1,1,1)$. Si l'un de ceux-là est codant, aucun des $ 4$ autres ne peut l'être. Donc on ne peut utiliser que $ 2$ éléments, par exemple $ (0,0,0,0)$ et $ (1,1,1,1)$. Si une coordonnée est changée, on pourra retrouver où est l'erreur et la corriger. Observons au passage que l'ensemble $ \{(0,0,0,0),(1,1,1,1)\}$ est un sous-espace vectoriel de dimension $ 1$ de $ (\mathbb{Z}/2\mathbb{Z})^4$ : c'est une «droite»  vectorielle.

Figure 5: Hypercube en dimension $ 4$. Chaque arête joint deux quadruplets qui diffèrent par une seule coordonnée.
\includegraphics[width=8cm,height=8cm]{hyper4}

Nous allons présenter un exemple de code correcteur d'erreur, le code de Hamming. Notre objectif sera surtout de relier ses propriétés aux applications linéaires sur l'espace vectoriel $ (\mathbb{Z}/2\mathbb{Z})^n$. Nous considérons le problème de coder les éléments de $ (\mathbb{Z}/2\mathbb{Z})^n$ par ceux de $ (\mathbb{Z}/2\mathbb{Z})^m$, donc de définir une application injective de $ (\mathbb{Z}/2\mathbb{Z})^n$ dans $ (\mathbb{Z}/2\mathbb{Z})^m$. Evidemment, $ m$ doit être plus grand que $ n$. Pour les codes de Hamming, on prend $ m=2^k-1$, et $ n=m-k$, où $ k$ est un certain entier. Nous prendrons l'exemple $ k=3$, donc nous coderons les $ 16$ éléments de $ (\mathbb{Z}/2\mathbb{Z})^4$ par autant d'éléments choisis dans $ (\mathbb{Z}/2\mathbb{Z})^7$ ($ 128$ éléments). Dans la pratique, on utilise les codes de Hamming pour des valeurs de $ k$ beaucoup plus élevées, et la «place perdue»  n'est pas aussi importante qu'il y paraît. Comme nous l'avons vu précédemment, si on veut pouvoir corriger une erreur, deux mots du code ne peuvent ni être voisins, ni avoir un voisin en commun. Ils doivent donc différer en au moins $ 3$ coordonnées. Nous devons donc trouver une application de $ (\mathbb{Z}/2\mathbb{Z})^4$ dans $ (\mathbb{Z}/2\mathbb{Z})^7$, telle que les images de deux vecteurs quelconques diffèrent en $ 3$ coordonnées au moins.

Dans toute la suite, les espaces vectoriels considérés sont munis de leur base canonique. Considérons l'application linéaire $ f$, de $ (\mathbb{Z}/2\mathbb{Z})^4$ dans $ (\mathbb{Z}/2\mathbb{Z})^7$, définie par la matrice $ A$ suivante.

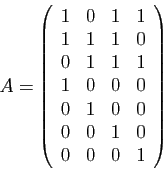
\begin{displaymath} A=\left( \begin{array}{cccc} 1&0&1&1\\ 1&1&1&0\\ 0&1&1&1\\ 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}\right) \end{displaymath}

Notons $ a_1,a_2,a_3,a_4$ les $ 4$ vecteurs colonnes de $ A$. Pour vérifier que $ f$ est injective, c'est-à-dire que son noyau est réduit au seul vecteur nul, il suffit de montrer que son image est de dimension $ 4$, ou encore que les vecteurs $ a_1,a_2,a_3,a_4$ forment une famille libre. On voit immédatement que c'est le cas en examinant leurs $ 4$ dernières coordonnées. Les 4 vecteurs $ a_1,a_2,a_3,a_4$ codent les 4 vecteurs de la base canonique de $ (\mathbb{Z}/2\mathbb{Z})^4$. Pour obtenir le code (l'image par $ f$) d'un autre vecteur de $ (\mathbb{Z}/2\mathbb{Z})^4$, il suffit de le multiplier par la matrice $ A$ (toutes les opérations se font dans $ \mathbb{Z}/2\mathbb{Z}$, c'est-à-dire modulo $ 2$). Voici par exemple le calcul de $ f(v)$, avec $ v=(1,1,0,1)$.

\begin{displaymath} \begin{array}{cc} & \left( \begin{array}{c} 1\\ 1\\ 0\\ 1... ... 0\\ 0\\ 0\\ 1\\ 1\\ 0\\ 1 \end{array}\right) \end{array}\end{displaymath}

Observons que les $ 4$ dernières lignes de la matrice $ A$ sont celles de la matrice identité en dimension $ 4$. Donc l'image par $ f$ d'un vecteur de $ 4$ bits quelconque se termine par ces mêmes $ 4$ bits. Les trois bits de tête sont des «bits de correction». Nous laissons au lecteur le soin de calculer les images par $ f$ des $ 16$ vecteurs de $ (\mathbb{Z}/2\mathbb{Z})^4$ et de vérifier que ces images diffèrent deux à deux en au moins $ 3$ bits. Pour comprendre comment fonctionne la correction d'erreur, il faut considérer l'application linéaire $ g$, de $ (\mathbb{Z}/2\mathbb{Z})^7$ dans $ (\mathbb{Z}/2\mathbb{Z})^3$, dont la matrice $ B$ est la suivante.

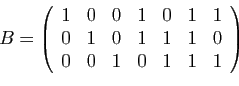
\begin{displaymath} B=\left( \begin{array}{ccccccc} 1&0&0&1&0&1&1\\ 0&1&0&1&1&1&0\\ 0&0&1&0&1&1&1 \end{array}\right) \end{displaymath}

Remarquez que les colonnes de $ B$ sont les écritures en base $ 2$ des entiers de $ 1$ à $ 7$.

Proposition 10   Le noyau de l'application $ g$ de matrice $ B$ et l'image de l'application $ f$ de matrice $ A$ sont le même sous-espace vectoriel de dimension $ 4$ de $ (\mathbb{Z}/2\mathbb{Z})^7$.

Démonstration : Il est facile de vérifier que l'image par $ g$ des 4 vecteurs $ a_1,a_2,a_3,a_4$ est le vecteur nul. Ceci entraîne que $ \mathrm{Im}(f)\subset \mathrm{Ker}(g)$. Il suffit alors de montrer que les dimensions de $ \mathrm{Im}(f)$ et $ \mathrm{Ker}(g)$ sont toutes deux égales à $ 4$. Nous l'avons déjà fait pour $ \mathrm{Im}(f)$. Pour $ \mathrm{Ker}(g)$, observons que les trois premiers vecteurs colonnes de $ B$ sont les $ 3$ vecteurs de la base canonique en dimension $ 3$. Donc $ \mathrm{Im}(g)$ a pour dimension $ 3$, et donc $ \mathrm{Ker}(g)$ a pour dimension $ 7-3=4$, d'après le théorème du rang. $ \square$

Par la proposition précédente, l'image par $ f$ d'un vecteur quelconque est dans le noyau de $ g$. Donc si un code a été correctement transmis, son image par $ g$ doit être nulle. Reprenons le vecteur $ v=(1,1,0,1)$ et supposons maintenant qu'une erreur a été commise sur son codage : au lieu de transmettre le vecteur $ f(v)=(0,0,0,1,1,0,1)$, on a transmis $ (0,0,0,1,0,0,1)$, c'est-à-dire que le cinquième bit a été changé : c'est $ f(v)+e_5$ qui a été transmis, avec $ e_5=(0,0,0,0,1,0,0)$. Puisque $ g(f(v))$ est le vecteur nul, l'image par $ g$ de $ f(v)+e_5$ est $ g(e_5)$, à savoir la cinquième colonne de $ B$. Etant donné un vecteur de $ 7$ bits reçu, on commence par prendre son image par $ g$ (en le multipliant par la matrice $ B$). Si cette image est nulle, alors il n'y a pas eu d'erreur de transmission, et il suffit de lire les $ 4$ derniers bits du vecteur transmis. Si l'image est égale à l'un des vecteurs colonnes de $ B$, disons le $ i$-ième, alors le $ i$-ième bit du vecteur reçu est faux : on le corrige et on lit ensuite les $ 4$ derniers bits du vecteur corrigé.


Section : Compléments
Avant : Dualité


         © UJF Grenoble, 2011                              Mentions légales