Relaxations Package for E-MicroM contains classes to compute the relaxation process linked with its stepper calls Times Package for E-MicroM . More...

Relaxations Package for E-MicroM contains classes to compute the relaxation process linked with its stepper calls Times Package for E-MicroM .

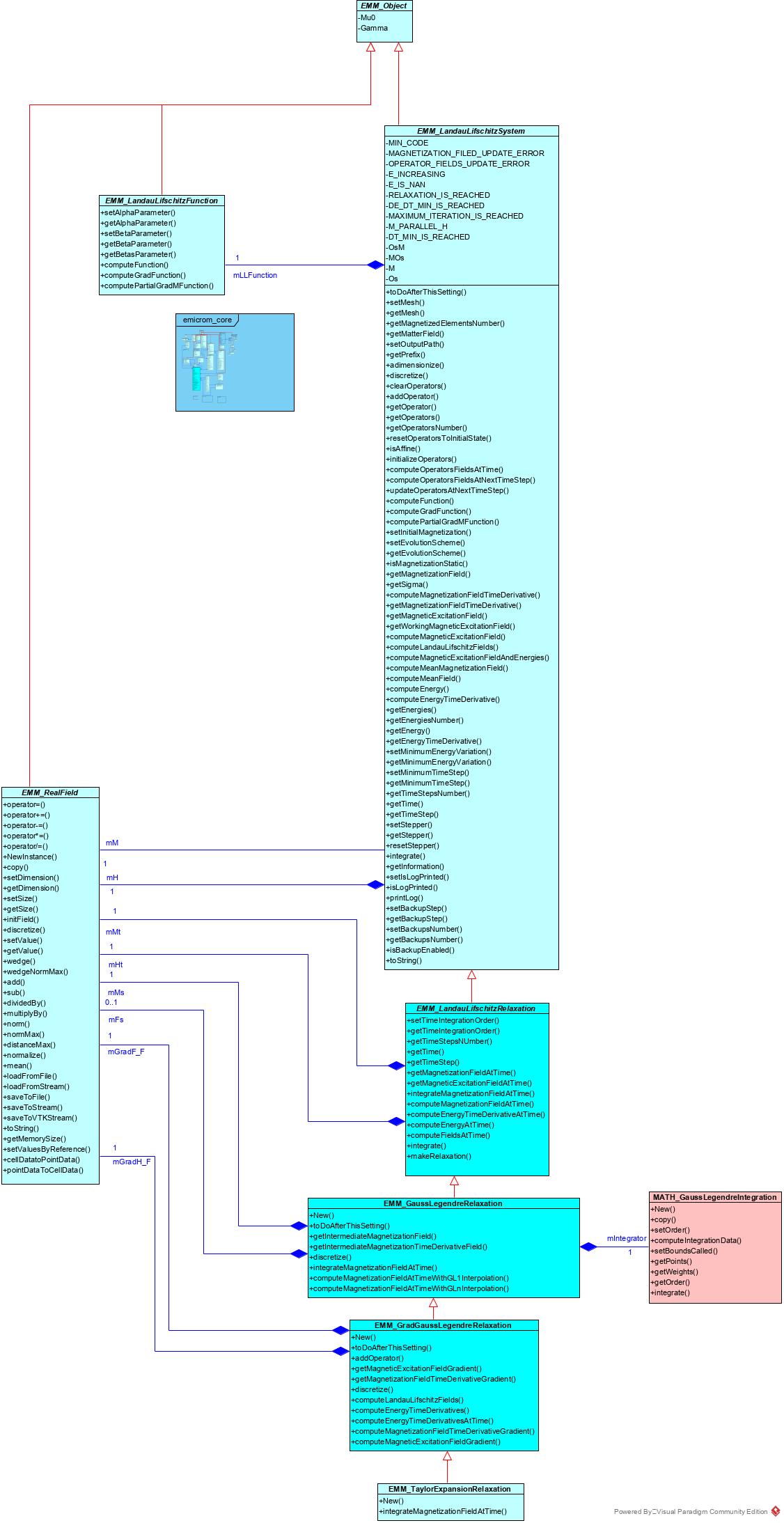
All systems inherit classes from EMM_LandauLifschitzRelaxation which implements the resolution of EMM_LandauLifschitzSystem

EMM_GaussLegendreRelaxation for general systems: the integral over time is computed with a Gauss-Legendre integration (see MATH_GaussLegendreIntegration from Mathematical Integration Package for E-MicroM )
EMM_GradGaussLegendreRelaxation for systems whose gradient of each operator with respect to M can be computed
EMM_TaylorExpansionRelaxation for affine systems: the integral with respect of time is computed thanks to a taylor expansion of 2 order.

There is 3 types of relaxation process depending on the operators. Each relaxation implements different ways to:

compute new time step of the interface method EMM_Stepper::computeNewDt() and
compute the new field M in the interface method EMM_LandauLifschitzRelaxation::computeMagnetizationFieldAtTime() which are specialized in inherited classes from EMM_LandauLifschitzRelaxation

EMM_TaylorExpansionRelaxation class makes a limited developpement at order 2 of the landau lifstchitz function to compute 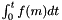$\int_0^t f(m) dt$ .

EMM_GaussLegendreRelaxation class makes the Gauss Legendre approximation of order k with many computations of the Landau Lifschitz function to compute 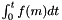$\int_0^t f(m) dt$

EMM_GradGaussLegendreRelaxation makes the Gauss Legendre approximation of order k with many computations of the Landau Lifschitz function to compute 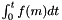$\int_0^t f(m) dt$ but it uses Gradient of H for computing the new time step.

If all excitation magnetic operators H are affines, computing the time step can be done by maximizing the energy variation (see EMM_OptimalTimeStep::computeNewTimeStep() )

If one excitation magnetic operator H is not affine, computing the time step can only be done by iterative method using the golden number iterative method or quadratic method to compute the time step which maximize the energy variation (see EMM_IterativeTimeStep::computeNewTimeStep() )

The systems package organization of this package is as follow: