Voici une autre situation où l'on rencontre des suites adjacentes
comme approximations numériques d'un réel. Nous allons construire par
récurrence une suite de rationnels 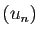 qui encadrent un réel
qui encadrent un réel 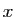 de manière optimale,
en un sens qui sera
précisé plus loin.
de manière optimale,
en un sens qui sera
précisé plus loin.
On construit d'abord une suite d'entiers 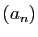 de la façon
suivante. Soit
de la façon
suivante. Soit 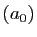 la partie entière de
la partie entière de 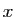 . On calcule
l'inverse de la partie décimale,
. On calcule
l'inverse de la partie décimale, 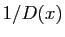 qui est un réel
supérieur à
qui est un réel
supérieur à 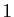 . On note
. On note 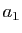 sa partie entière. On itère
ensuite le procédé, en prenant pour chaque entier la partie
entière de l'inverse de la partie décimale.
Voici ce que cela donne pour
sa partie entière. On itère
ensuite le procédé, en prenant pour chaque entier la partie
entière de l'inverse de la partie décimale.
Voici ce que cela donne pour 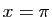 .
.
Vous pourrez vérifier que la suite 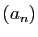 associée à
associée à
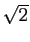 est
est
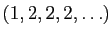 .
La suite associée au nombre d'or
.
La suite associée au nombre d'or
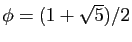 est
est
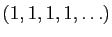 .
La suite des entiers
.
La suite des entiers
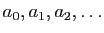 étant donnée, on
fabrique une suite de rationnels
étant donnée, on
fabrique une suite de rationnels  en reprenant le processus à
l'envers.
en reprenant le processus à
l'envers.
Le terme général  est
est
Le terme «fraction continue» est assez clair. Il n'y a pourtant pas
de rapport direct avec les fonctions continues. Il vaudrait mieux dire, comme
en anglais, «fraction continuée».
Voici les premiers termes de la suite 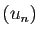 pour
pour 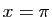 , et la valeur numérique de
, et la valeur numérique de
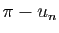 .
Le premier terme
.
Le premier terme 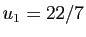 était déjà connu d'Archimède
comme approximation de
était déjà connu d'Archimède
comme approximation de 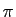 . Le troisième,
. Le troisième, 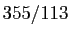 a été proposé
par Adrien Métius en 1624. Les Chinois, tel Zu Zhong Chi au Ve
siècle, connaissaient ces deux approximations. L'exemple tel que
nous le présentons, figure dans un texte écrit par
Leonhard Euler (1707-1783) en 1748.
a été proposé
par Adrien Métius en 1624. Les Chinois, tel Zu Zhong Chi au Ve
siècle, connaissaient ces deux approximations. L'exemple tel que
nous le présentons, figure dans un texte écrit par
Leonhard Euler (1707-1783) en 1748.
Les  s'approchent rapidement de
s'approchent rapidement de 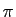 , et de plus ils encadrent
la valeur exacte : les deux sous-suites
, et de plus ils encadrent
la valeur exacte : les deux sous-suites 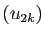 et
et
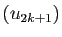 sont adjacentes. On démontre le résultat suivant.
sont adjacentes. On démontre le résultat suivant.
Cet encadrement montre que l'erreur commise en
approchant 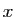 par
par  est majoré par l'inverse du
carré du dénominateur.
La taille du dénominateur est en quelque sorte le prix que l'on
accepte de payer
pour une approximation rationnelle de
est majoré par l'inverse du
carré du dénominateur.
La taille du dénominateur est en quelque sorte le prix que l'on
accepte de payer
pour une approximation rationnelle de 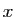 . On démontre que parmi les
rationnels dont le dénominateur est inférieur ou égal à
. On démontre que parmi les
rationnels dont le dénominateur est inférieur ou égal à 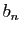 ,
c'est
,
c'est  qui est le plus proche de
qui est le plus proche de 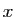 . L'approximation par
fractions continues est donc la meilleure possible.
. L'approximation par
fractions continues est donc la meilleure possible.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() qui encadrent un réel
qui encadrent un réel ![]() de manière optimale,
en un sens qui sera
précisé plus loin.
de manière optimale,
en un sens qui sera
précisé plus loin.
![]() de la façon
suivante. Soit
de la façon
suivante. Soit ![]() la partie entière de
la partie entière de ![]() . On calcule
l'inverse de la partie décimale,
. On calcule
l'inverse de la partie décimale, ![]() qui est un réel
supérieur à
qui est un réel
supérieur à ![]() . On note
. On note ![]() sa partie entière. On itère
ensuite le procédé, en prenant pour chaque entier la partie
entière de l'inverse de la partie décimale.
Voici ce que cela donne pour
sa partie entière. On itère
ensuite le procédé, en prenant pour chaque entier la partie
entière de l'inverse de la partie décimale.
Voici ce que cela donne pour ![]() .
.
![\begin{displaymath}
\begin{array}{lll}
a_0 = \lfloor \pi \rfloor &= 3 & d_0=\pi-...
...x]
a_5 = \lfloor 1/d_4 \rfloor &= 1 & d_5=1/d_4-a_5
\end{array}\end{displaymath}](img769.gif)
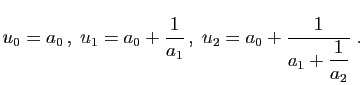
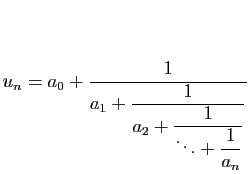
![\begin{displaymath}
\begin{array}{\vert c\vert cr\vert}
\hline
n&u_n&\multicolum...
...frac{104348}{33215}& -0.0000000003\ [1.5ex]
\hline
\end{array}\end{displaymath}](img780.gif)
![]() , notons
, notons ![]() et
et ![]() les deux
entiers premiers entre eux tels que
les deux
entiers premiers entre eux tels que
![]() . Alors :
. Alors :
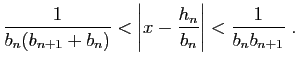
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales