Nous utilisons à nouveau les déterminants.
La définition 5 semble dépendre du choix
d'une base particulière. Nous ne considérons ici que des bases
orthonormées. Observons que
Det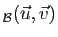 est
le produit scalaire du vecteur
est
le produit scalaire du vecteur  par le vecteur
par le vecteur 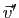 , de coordonnées
, de coordonnées
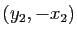 . Or
. Or
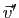 est l'un des deux vecteurs orthogonaux à
est l'un des deux vecteurs orthogonaux à
 , de même norme que
, de même norme que  . La
proposition 8 montre que le produit scalaire,
et donc l'orthogonalité et la norme ne dépendent pas de la base
orthonormée dans laquelle on écrit les vecteurs. Ceci entraîne
que le calcul de
Det
. La
proposition 8 montre que le produit scalaire,
et donc l'orthogonalité et la norme ne dépendent pas de la base
orthonormée dans laquelle on écrit les vecteurs. Ceci entraîne
que le calcul de
Det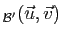 donnera soit le même résultat, soit l'opposé,
si on exprime les vecteurs dans une autre base
orthonormée
donnera soit le même résultat, soit l'opposé,
si on exprime les vecteurs dans une autre base
orthonormée 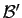 .
Ceci permet de définir l'orientation du
plan, à partir d'une seule base de référence.
Nous supposons désormais que le plan est muni d'une base
orthonormée
.
Ceci permet de définir l'orientation du
plan, à partir d'une seule base de référence.
Nous supposons désormais que le plan est muni d'une base
orthonormée 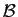 , et nous omettons l'indice
, et nous omettons l'indice 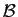 dans l'écriture des déterminants.
dans l'écriture des déterminants.
Définition 15
Soient  et
et  deux
vecteurs non colinéaires. On dit du couple
deux
vecteurs non colinéaires. On dit du couple
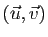 qu'il
est une base directe si
qu'il
est une base directe si
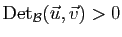 .
.
Observons que si
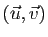 est une base directe, alors
est une base directe, alors
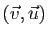 ne l'est pas, d'après le point b) de
la proposition 2.
ne l'est pas, d'après le point b) de
la proposition 2.
La valeur du déterminant s'interprète
géométriquement grâce à la formule suivante, qui se déduit
immédiatement de (9).
Det
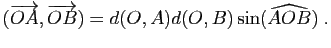
 (figure
6).
(figure
6).
Figure 6:
La valeur absolue du déterminant
est l'aire du parallélogramme.
|
|
Nous avons déjà rencontré des déterminants pour établir
l'équation implicite d'un plan dans l'espace.
Pour calculer le produit vectoriel
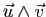 , retenez que sa première
coordonnée est le déterminant des deux dernières coordonnées
de
, retenez que sa première
coordonnée est le déterminant des deux dernières coordonnées
de  et
et  , puis écrivez les
deux coordonnées suivantes en permutant deux fois circulairement
, puis écrivez les
deux coordonnées suivantes en permutant deux fois circulairement
 .
.
Les propriétés du produit vectoriel en dimension 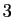 rappellent
celles du déterminant en dimension
rappellent
celles du déterminant en dimension 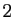 .
.
Proposition 12
- Le produit vectoriel est changé en son opposé
si on permute les deux vecteurs
- le produit vectoriel est bilinéaire
- Le produit vectoriel
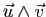 est le vecteur nul
si et seulement si
est le vecteur nul
si et seulement si  et
et  sont
colinéaires.
sont
colinéaires.
Nous avons déjà observé que le vecteur
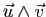 est orthogonal à
est orthogonal à
 et
et  (lemme 1).
Sa norme est la
surface du parallélogramme construit à partir des deux vecteurs
(cf. figure 6).
Passons maintenant à la dimension
(lemme 1).
Sa norme est la
surface du parallélogramme construit à partir des deux vecteurs
(cf. figure 6).
Passons maintenant à la dimension 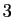 .
Soit
.
Soit  un espace vectoriel de dimension
un espace vectoriel de dimension 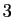 muni
d'une base orthonormée
muni
d'une base orthonormée
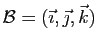 . Nous continuons
à omettre l'indice
. Nous continuons
à omettre l'indice 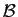 dans l'écriture des déterminants.
La proposition suivante consiste simplement à écrire la
définition 6 à l'aide des produits scalaire et vectoriel.
dans l'écriture des déterminants.
La proposition suivante consiste simplement à écrire la
définition 6 à l'aide des produits scalaire et vectoriel.
L'expression
Det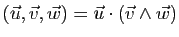 permet de donner une
interprétation géométrique du déterminant en dimension
permet de donner une
interprétation géométrique du déterminant en dimension 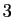 ,
analogue à la dimension
,
analogue à la dimension 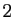 : la valeur absolue du
déterminant de
: la valeur absolue du
déterminant de 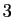 vecteurs
vecteurs
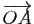 ,
,
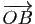 ,
,
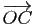 est le volume du parallélépipède de sommets
est le volume du parallélépipède de sommets 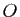 ,
,  ,
, 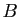 ,
, 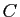 ,
,
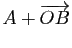 ,
,
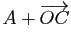 ,
,
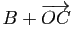 ,
,
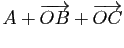 (figure
7). Le signe est positif si les
(figure
7). Le signe est positif si les 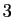 vecteurs sont
orientés dans le sens direct (comme sur la figure
7), négatif s'il est orienté dans
le sens indirect (rappelons que le déterminant change de signe si on
permute
vecteurs sont
orientés dans le sens direct (comme sur la figure
7), négatif s'il est orienté dans
le sens indirect (rappelons que le déterminant change de signe si on
permute 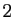 des
des 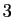 vecteurs). Le signe du déterminant permet donc
d'orienter une base quelconque, par rapport à une base de
référence. L'orientation de la base de référence se fait selon
la règle du bonhomme d'Ampère, autrement nommé
tire-bouchon de Maxwell.
vecteurs). Le signe du déterminant permet donc
d'orienter une base quelconque, par rapport à une base de
référence. L'orientation de la base de référence se fait selon
la règle du bonhomme d'Ampère, autrement nommé
tire-bouchon de Maxwell.
Définition 17
Soit  un espace vectoriel de dimension
un espace vectoriel de dimension 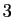 , muni d'une base
, muni d'une base
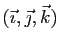 . Soient
. Soient
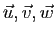 trois
vecteurs non coplanaires. On dit du triplet
trois
vecteurs non coplanaires. On dit du triplet
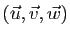 qu'il est une base directe si
qu'il est une base directe si
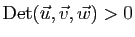 .
.
Figure 7:
La valeur absolue du déterminant
est le volume du parallélépipède.
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() rappellent
celles du déterminant en dimension
rappellent
celles du déterminant en dimension ![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales