Commençons par la définition d'un produit scalaire.
Observez que si 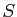 est symétrique, et linéaire par rapport à
l'une des composantes, elle est nécessairement linéaire par
rapport à l'autre.
est symétrique, et linéaire par rapport à
l'une des composantes, elle est nécessairement linéaire par
rapport à l'autre.
Soit  un espace vectoriel de dimension
un espace vectoriel de dimension 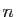 , muni d'une
base
, muni d'une
base
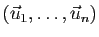 . Soient
. Soient  et
et  deux vecteurs de
deux vecteurs de  .
.
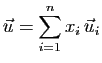
et
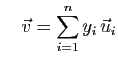
On
appelle produit scalaire de  et
et  relatif à la base
relatif à la base
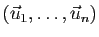 , et on note
, et on note
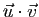 la somme des produits deux à
deux des coordonnées.
la somme des produits deux à
deux des coordonnées.
Il est immédiat de vérifier que le produit scalaire relatif à une
base, vérifie bien la définition
9. On démontre que si 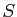 est un produit scalaire au sens de la définition
9, sur un espace de dimension finie,
alors il existe une base
est un produit scalaire au sens de la définition
9, sur un espace de dimension finie,
alors il existe une base 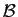 telle que
telle que
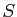 soit le produit scalaire relatif à la base
soit le produit scalaire relatif à la base 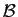 . En
dimension finie, quitte à changer de base, on se ramène donc
toujours au cas où le produit scalaire est la
somme des produits deux à deux des coordonnées. Nous noterons donc
désormais
. En
dimension finie, quitte à changer de base, on se ramène donc
toujours au cas où le produit scalaire est la
somme des produits deux à deux des coordonnées. Nous noterons donc
désormais
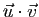 le produit
scalaire de deux vecteurs, comme vous en avez l'habitude.
Dans un espace vectoriel, la donnée d'un
produit scalaire induit les notions d'orthogonalité, et
de norme.
le produit
scalaire de deux vecteurs, comme vous en avez l'habitude.
Dans un espace vectoriel, la donnée d'un
produit scalaire induit les notions d'orthogonalité, et
de norme.
Comme conséquence du fait qu'un produit scalaire est défini
positif, la norme d'un vecteur ne peut être nulle que si ce vecteur
est nul. De même, si deux vecteurs sont à la fois orthogonaux et
colinéaires alors l'un d'entre eux est le vecteur nul ; ou de
manière équivalente, si deux vecteurs non nuls sont orthogonaux,
ils ne sont pas colinéaires.
Considérons un espace vectoriel de dimension 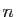 , muni d'une base
, muni d'une base
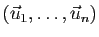 et notons
et notons
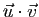 le produit scalaire
relatif à cette base.
le produit scalaire
relatif à cette base.
Dans la base
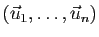 , le vecteur
, le vecteur
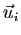 a toutes ses coordonnées nulles, sauf la
a toutes ses coordonnées nulles, sauf la 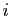 -ième qui
vaut
-ième qui
vaut 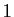 . On vérifie donc
immédiatement que
. On vérifie donc
immédiatement que 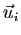 a pour norme
a pour norme 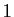 et que
et que 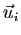 et
et
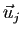 sont orthogonaux pour
sont orthogonaux pour 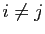 .
On dit que la base est orthonormée.
.
On dit que la base est orthonormée.
Tel que nous l'avons défini, le produit scalaire semble dépendre
de la base. La proposition suivante montre que si on remplace la
base initiale par une autre base orthonormée, le produit scalaire
garde la même écriture.
Démonstration : En utilisant la bilinéarité:
car puisque la base est orthonormée,

Voici un résultat souvent utile, l'inégalité de
Cauchy-Schwarz.
Démonstration : Soit 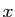 un réel quelconque. Calculons le produit scalaire du
vecteur
un réel quelconque. Calculons le produit scalaire du
vecteur
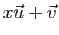 par lui-même, en
utilisant la bilinéarité et la symétrie:
par lui-même, en
utilisant la bilinéarité et la symétrie:
Cette expression est un polynôme du second degré en 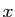 . Or pour
tout
. Or pour
tout 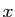 , il prend une valeur positive ou nulle. Son discriminant ne
peut pas être strictement positif,
car sinon le polynôme aurait deux racines
réelles entre lesquelles il prendrait des valeurs
négatives. Ecrire que le discriminant est négatif ou nul donne:
, il prend une valeur positive ou nulle. Son discriminant ne
peut pas être strictement positif,
car sinon le polynôme aurait deux racines
réelles entre lesquelles il prendrait des valeurs
négatives. Ecrire que le discriminant est négatif ou nul donne:
soit
ce qui entraîne (8). L'égalité a lieu
si et seulement si le trinôme admet une racine double 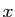 ,
valeur pour laquelle
,
valeur pour laquelle
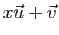 est le vecteur nul.
est le vecteur nul. 
Passons maintenant à l'espace affine. Rappelons qu'un repère est
constitué d'une origine 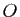 et d'une base de l'espace vectoriel
associé.
Dire qu'on munit l'espace d'un
repère orthonormé, c'est supposer
implicitement qu'on dispose d'un produit scalaire, pour lequel les
vecteurs de la base sont orthogonaux deux à deux, et de norme
et d'une base de l'espace vectoriel
associé.
Dire qu'on munit l'espace d'un
repère orthonormé, c'est supposer
implicitement qu'on dispose d'un produit scalaire, pour lequel les
vecteurs de la base sont orthogonaux deux à deux, et de norme 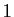 .
Ceci permet de définir la distance euclidienne.
.
Ceci permet de définir la distance euclidienne.
Définition 12
Soit  un espace affine, muni d'un repère orthonormé.
On appelle distance euclidienne
de deux points
un espace affine, muni d'un repère orthonormé.
On appelle distance euclidienne
de deux points  et
et 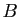 , et on note
, et on note 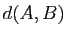 ,
la norme du vecteur
,
la norme du vecteur
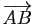 .
.
Vous apprendrez plus tard qu'il existe de multiples manières de
définir une distance dans un espace. Pour l'instant, nous
n'utiliserons que celle-ci, et nous omettrons
l'adjectif «euclidienne».
L'inégalité de Cauchy-Schwarz montre que le rapport entre le
produit scalaire de deux vecteurs non nuls
et le produit de leurs normes est
compris entre 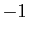 et
et 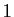 . Ce rapport est interprété comme
le cosinus de l'angle
que forment les deux vecteurs.
. Ce rapport est interprété comme
le cosinus de l'angle
que forment les deux vecteurs.
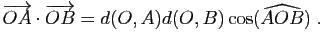 |
(9) |
Cette interprétation permet de retrouver
tous les résultats classiques de la géométrie plane ;
par exemple le théorème suivant, dit théorème d'Al-Kashi
(figure 4).
Le cas particulier où le triangle est rectangle en  (
(
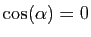 ) est le théorème du regretté Pythagore.
Démonstration : La relation de Chasles donne :
) est le théorème du regretté Pythagore.
Démonstration : La relation de Chasles donne :
En utilisant la bilinéarité du produit scalaire, on écrit:

Figure:
Le théorème d'Al-Kashi:
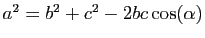 .
.
|
|
Définir rigoureusement la notion d'angle de deux
vecteurs pose un problème de choix d'orientation.
En dimension 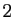 les angles sont mesurés de 0
à
les angles sont mesurés de 0
à 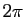 , dans le sens trigonométrique. En dimension
, dans le sens trigonométrique. En dimension 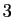 ,
parler d'angle dans un plan suppose qu'on a défini
une orientation du plan, ce qui peut se faire si on a défini
une orientation de l'espace, et une orientation normale du
plan.
Deux ensembles de vecteurs sont dits orthogonaux si tout vecteur de
l'un est orthogonal à tout vecteur de l'autre. Nous examinons le cas
particulier de deux droites vectorielles dans un plan. Observons que, du
fait de la bilinéarité, si deux vecteurs sont orthogonaux, tout
vecteur colinéaire à l'un est orthogonal à tout vecteur
colinéaire à l'autre.
,
parler d'angle dans un plan suppose qu'on a défini
une orientation du plan, ce qui peut se faire si on a défini
une orientation de l'espace, et une orientation normale du
plan.
Deux ensembles de vecteurs sont dits orthogonaux si tout vecteur de
l'un est orthogonal à tout vecteur de l'autre. Nous examinons le cas
particulier de deux droites vectorielles dans un plan. Observons que, du
fait de la bilinéarité, si deux vecteurs sont orthogonaux, tout
vecteur colinéaire à l'un est orthogonal à tout vecteur
colinéaire à l'autre.
Réciproquement, l'ensemble des vecteurs du plan,
orthogonaux à un vecteur
donné est une droite vectorielle.
Définition 13
On dit que deux droites du plan affine sont orthogonales (ou
perpendiculaires) si tout vecteur
directeur de l'une est orthogonal à tout vecteur directeur de l'autre.
La projection orthogonale utilise le fait qu'il existe une seule
perpendiculaire à une droite donnée passant par un point
extérieur à cette droite (figure
5).
Définition 14
Soit 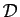 une droite et
une droite et  un point du plan, n'appartenant pas
à
un point du plan, n'appartenant pas
à 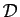 .
on appelle projection orthogonale de
.
on appelle projection orthogonale de  sur
sur 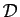 le point d'intersection de
le point d'intersection de 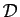 avec la droite orthogonale à
avec la droite orthogonale à
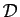 passant par
passant par  .
On appelle distance du point
.
On appelle distance du point  à la droite
à la droite 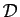 la distance du
point à sa projection orthogonale sur la droite.
la distance du
point à sa projection orthogonale sur la droite.
On étend cette définition de façon évidente aux points de
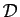 : la projection orthogonale d'un point de
: la projection orthogonale d'un point de 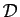 sur
sur 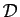 est le point lui-même, et sa distance à
est le point lui-même, et sa distance à 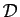 est nulle.
Le théorème de Pythagore entraîne que la distance d'un point
à une droite est la plus petite des distances de ce point à un
point de la droite. Dans le cas où la droite est définie par une
équation implicite, la distance d'un point à cette droite se
calcule très simplement.
est nulle.
Le théorème de Pythagore entraîne que la distance d'un point
à une droite est la plus petite des distances de ce point à un
point de la droite. Dans le cas où la droite est définie par une
équation implicite, la distance d'un point à cette droite se
calcule très simplement.
Démonstration : Si
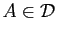 la distance est nulle, et la formule est vraie. Supposons
maintenant que le point
la distance est nulle, et la formule est vraie. Supposons
maintenant que le point  n'appartienne pas à la droite
n'appartienne pas à la droite 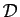 (figure
5).
Le vecteur de coordonnées
(figure
5).
Le vecteur de coordonnées 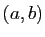 , que nous
noterons
, que nous
noterons 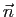 , est orthogonal au vecteur de
coordonnées
, est orthogonal au vecteur de
coordonnées 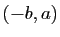 , qui est un vecteur directeur de la droite
(
, qui est un vecteur directeur de la droite
(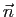 pour «normal» : un autre synonyme
d'orthogonal). Notons
pour «normal» : un autre synonyme
d'orthogonal). Notons 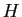 la projection orthogonale
de
la projection orthogonale
de  sur
sur 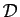 . Tout point
. Tout point 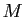 de la droite vérifie :
de la droite vérifie :
car
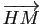 et
et 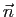 sont
orthogonaux. Comme
sont
orthogonaux. Comme
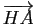 et
et 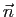 sont
colinéaires, la valeur absolue de leur produit scalaire est le
produit des normes. On obtient donc :
sont
colinéaires, la valeur absolue de leur produit scalaire est le
produit des normes. On obtient donc :
Par définition,
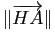 est la distance de
est la distance de  à
la droite, et
à
la droite, et
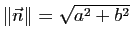 . Il reste à
évaluer le produit scalaire de
. Il reste à
évaluer le produit scalaire de
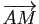 par
par
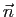 .
.
car
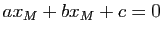 . D'où le résultat.
. D'où le résultat.
Figure 5:
Projection orthogonale d'un point sur une droite.
|
|
Les notions de projection orthogonale et de distance sont définies
de la même façon en dimension  . Soient deux vecteurs
. Soient deux vecteurs
 et
et  , non colinéaires, et
, non colinéaires, et
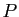 le plan vectoriel qu'ils engendrent.
le plan vectoriel qu'ils engendrent.
Nous avons introduit à la section précédente les trois
coefficients :
Ce sont trois déterminants.
Puisque  et
et  ne sont pas colinéaires, la proposition 1 entraîne
que
ne sont pas colinéaires, la proposition 1 entraîne
que 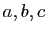 ne sont pas tous les trois nuls.
Les deux relations :
ne sont pas tous les trois nuls.
Les deux relations :
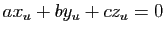
et
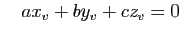
montrent que le vecteur 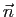 de coordonnées
de coordonnées
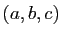 est orthogonal à
est orthogonal à  et
à
et
à  (voir lemme 1).
La bilinéarité du produit scalaire
entraîne que
(voir lemme 1).
La bilinéarité du produit scalaire
entraîne que 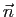 est orthogonal à tout vecteur
de
est orthogonal à tout vecteur
de 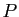 . Réciproquement, tout vecteur orthogonal à
. Réciproquement, tout vecteur orthogonal à
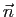 est combinaison linéaire de
est combinaison linéaire de  et
et
 , et donc appartient à
, et donc appartient à
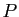 .
.
Soit 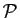 un plan affine dans un espace de dimension
un plan affine dans un espace de dimension 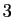 ,
et
,
et  un point n'appartenant pas à
un point n'appartenant pas à 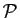 . La
projection orthogonale de
. La
projection orthogonale de  sur
sur 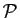 est
l'intersection avec
est
l'intersection avec 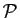 de la droite
passant par
de la droite
passant par  et de vecteur directeur
et de vecteur directeur 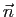 (la
perpendiculaire à
(la
perpendiculaire à 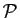 passant par
passant par  ).
La distance d'un point à un plan défini par une équation
implicite se calcule par une formule analogue à celle de la
proposition 9.
).
La distance d'un point à un plan défini par une équation
implicite se calcule par une formule analogue à celle de la
proposition 9.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
 ,
,  ,
,
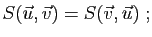
 ,
,  ,
,
 et tous réels
et tous réels  ,
, 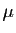 ,
,
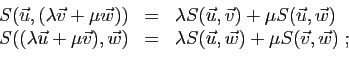
 ,
,
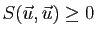 et
et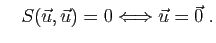
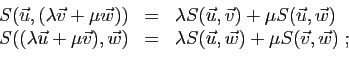
![]() un espace vectoriel de dimension
un espace vectoriel de dimension ![]() , muni d'une
base
, muni d'une
base
![]() . Soient
. Soient ![]() et
et ![]() deux vecteurs de
deux vecteurs de ![]() .
.
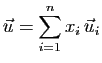 et
et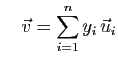
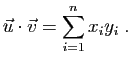
![]() , le vecteur
, le vecteur
![]() a toutes ses coordonnées nulles, sauf la
a toutes ses coordonnées nulles, sauf la ![]() -ième qui
vaut
-ième qui
vaut ![]() . On vérifie donc
immédiatement que
. On vérifie donc
immédiatement que ![]() a pour norme
a pour norme ![]() et que
et que ![]() et
et
![]() sont orthogonaux pour
sont orthogonaux pour ![]() .
On dit que la base est orthonormée.
.
On dit que la base est orthonormée.
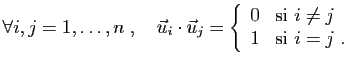
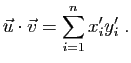
![\begin{displaymath}
\begin{array}{lcl}
\vec{u}\cdot\vec{v}&=&
\displaystyle{\lef...
... [2ex]
&=&
\displaystyle{
\sum_{i=1}^n x'_iy'_i\;,}
\end{array}\end{displaymath}](img296.gif)
![]() et d'une base de l'espace vectoriel
associé.
Dire qu'on munit l'espace d'un
repère orthonormé, c'est supposer
implicitement qu'on dispose d'un produit scalaire, pour lequel les
vecteurs de la base sont orthogonaux deux à deux, et de norme
et d'une base de l'espace vectoriel
associé.
Dire qu'on munit l'espace d'un
repère orthonormé, c'est supposer
implicitement qu'on dispose d'un produit scalaire, pour lequel les
vecteurs de la base sont orthogonaux deux à deux, et de norme ![]() .
Ceci permet de définir la distance euclidienne.
.
Ceci permet de définir la distance euclidienne.
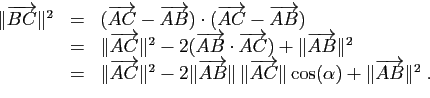
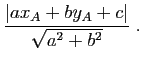
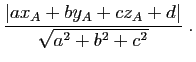
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales