En dimension 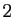 ,
il faut voir un système de coordonnées comme une
application de
l'ensemble des couples de réels
,
il faut voir un système de coordonnées comme une
application de
l'ensemble des couples de réels
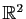 (ou un de ses
sous-ensembles) vers l'ensemble des points
du plan: à un couple de réels l'application associe un point
du plan et un seul.
Moyennant le choix d'un repère orthonormé
(ou un de ses
sous-ensembles) vers l'ensemble des points
du plan: à un couple de réels l'application associe un point
du plan et un seul.
Moyennant le choix d'un repère orthonormé
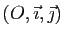 , l'application qui à un
couple de réels
, l'application qui à un
couple de réels 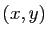 associe le point
associe le point 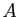 du plan tel que :
du plan tel que :
est une application de
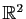 vers le plan. Cette application est
bijective: à tout point du
plan correspond un unique couple de réels.
vers le plan. Cette application est
bijective: à tout point du
plan correspond un unique couple de réels.
De même dans un espace de dimension 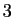 muni d'un repère
muni d'un repère
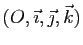 ,
l'application qui à un triplet de
réels
,
l'application qui à un triplet de
réels 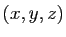 associe le point
associe le point 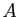 tel que :
tel que :
est une bijection de
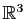 vers l'espace. Ces applications sont les
systèmes de coordonnées cartésiennes.
vers l'espace. Ces applications sont les
systèmes de coordonnées cartésiennes.
On rencontre souvent en physique des situations où les calculs
s'effectuent plus simplement en utilisant d'autres systèmes de
coordonnées. Nous allons présenter les plus courants: les
coordonnées polaires dans le plan, les coordonnées cylindriques
et sphériques en dimension 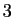 .
Elles sont définies par référence
aux coordonnées cartésiennes.
Les coordonnées polaires sont la traduction géométrique de la forme
trigonométrique des nombres complexes. Supposons le plan muni d'un repère
.
Elles sont définies par référence
aux coordonnées cartésiennes.
Les coordonnées polaires sont la traduction géométrique de la forme
trigonométrique des nombres complexes. Supposons le plan muni d'un repère
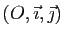 . Voici l'application qui
aux coordonnées polaires associe les coordonnées cartésiennes
(figure 8).
. Voici l'application qui
aux coordonnées polaires associe les coordonnées cartésiennes
(figure 8).
Les réels 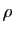 et
et 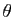 sont le module et l'argument de l'affixe
du point de coordonnées cartésiennes
sont le module et l'argument de l'affixe
du point de coordonnées cartésiennes 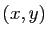 :
: 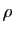 est la distance
de l'origine au point et
est la distance
de l'origine au point et 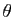 est l'angle orienté entre le
vecteur
est l'angle orienté entre le
vecteur
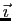 et le vecteur
et le vecteur
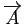 .
Observons que l'application ainsi définie n'est pas
(tout à fait) bijective: tout couple
.
Observons que l'application ainsi définie n'est pas
(tout à fait) bijective: tout couple 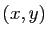 a
un antécédent unique, sauf
a
un antécédent unique, sauf 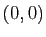 qui a pour antécédents tous
les couples
qui a pour antécédents tous
les couples
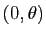 . Si on la restreint aux valeurs de
. Si on la restreint aux valeurs de 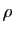 strictement positives, l'application définie ci-dessus est
bien une bijection de
strictement positives, l'application définie ci-dessus est
bien une bijection de
![$ ]0,+\infty[\times [0,2\pi[$](img379.gif) vers le
plan privé de l'origine.
vers le
plan privé de l'origine.
Figure 8:
Coordonnées polaires d'un point du plan.
|
|
Les coordonnées
cylindriques remplacent les deux premières
des trois coordonnées cartésiennes
par les coordonnées polaires correspondantes, en
conservant la troisième (figure
9)
Cette application n'est toujours pas une bijection, puisque l'image
réciproque de 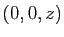 est l'ensemble des triplets de la forme
est l'ensemble des triplets de la forme
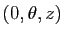 ,
,
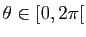 .
.
Figure 9:
Coordonnées cylindriques d'un point de l'espace.
|
|
Les coordonnées sphériques suivent la même logique que
les coordonnées polaires: la première des trois
est la distance de l'origine au point. Les deux autres sont
deux angles, correspondant à la
longitude et la co-latitude terrestres (figure
10).
Figure 10:
Coordonnées sphériques d'un point de l'espace.
|
|
Cette application n'est pas plus bijective que les précédentes
(la latitude et la longitude ne sont pas définies de façon
unique au centre de la terre).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() muni d'un repère
muni d'un repère
![]() ,
l'application qui à un triplet de
réels
,
l'application qui à un triplet de
réels ![]() associe le point
associe le point ![]() tel que :
tel que :
![]() .
Elles sont définies par référence
aux coordonnées cartésiennes.
Les coordonnées polaires sont la traduction géométrique de la forme
trigonométrique des nombres complexes. Supposons le plan muni d'un repère
.
Elles sont définies par référence
aux coordonnées cartésiennes.
Les coordonnées polaires sont la traduction géométrique de la forme
trigonométrique des nombres complexes. Supposons le plan muni d'un repère
![]() . Voici l'application qui
aux coordonnées polaires associe les coordonnées cartésiennes
(figure 8).
. Voici l'application qui
aux coordonnées polaires associe les coordonnées cartésiennes
(figure 8).
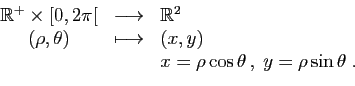
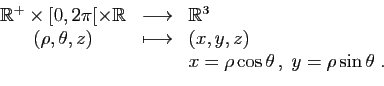
![\begin{displaymath}
\begin{array}{ccl}
\mathbb{R}^+\times [0,2\pi[\times [0,\pi]...
...phi ,\;y=r\sin\theta\sin\phi
,\;z=r\cos\theta\;.
\end{array}\end{displaymath}](img386.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales