Dans cette section, nous définissons la notion de déterminant,
puis nous en déduisons un critère pratique pour
reconnaître une base, dans un espace
vectoriel de dimension 2 ou 3. Nous commençons par la dimension 2.
Démonstration : Soient 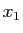 et
et 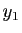 deux réels.
deux réels.
Donc, pour tout  de
de  ,
,
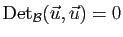 , ce qui démontre a).
De même, la relation
, ce qui démontre a).
De même, la relation
entraîne l'assertion b).
Soient 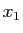 ,
, 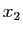 ,
, 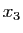 ,
, 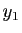 ,
, 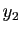 ,
, 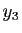 ,
,
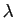 et
et 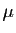 des nombres réels. L'assertion
c) découle des égalités :
des nombres réels. L'assertion
c) découle des égalités :
Reprenons les notations de l'assertion d).
Soient 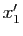 ,
, 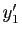 (resp.
(resp. 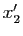 ,
, 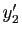 )
les coordonnées de
)
les coordonnées de  (resp.
(resp.  )
dans la base
)
dans la base 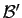 .
.
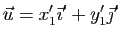
et
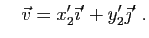
En appliquant c), b) et a) on obtient :

Corollaire 1
Soit
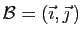 une base de
une base de  .
Pour tous
.
Pour tous  ,
,  de
de  ,
,
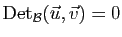 si et seulement si
si et seulement si
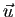 et
et 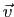 sont colinéaires.
sont colinéaires.
Démonstration : Si 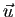 et
et 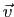 sont colinéaires, alors
il existe
sont colinéaires, alors
il existe
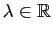 tel que
tel que
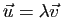 ou
ou
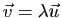 . Dans les deux cas, il résulte
des assertions a) et c) de la proposition que
. Dans les deux cas, il résulte
des assertions a) et c) de la proposition que
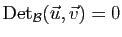 .
.
Si 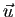 et
et 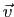 ne sont pas colinéaires,
alors la famille
ne sont pas colinéaires,
alors la famille
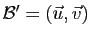 est une base
de
est une base
de  . Par la relation d), on obtient que :
. Par la relation d), on obtient que :
Par conséquent,
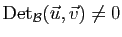 .
.
Passons maintenant à la dimension 3. Soit  un espace vectoriel de dimension
un espace vectoriel de dimension 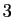 (par exemple
(par exemple
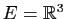 ).
Soient
).
Soient 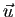 ,
, 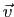 et
et 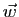 des vecteurs de
des vecteurs de  .
La famille
.
La famille
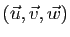 est liée si et seulement
si les trois vecteurs sont coplanaires, ou encore si et
seulement si un de ces vecteurs
est une combinaison linéaire des deux autres.
est liée si et seulement
si les trois vecteurs sont coplanaires, ou encore si et
seulement si un de ces vecteurs
est une combinaison linéaire des deux autres.
Définition 6
Soit
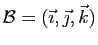 une base
de l'espace vectoriel
une base
de l'espace vectoriel  . Soient
. Soient 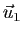 ,
, 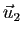 et
et 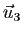 des vecteurs de
des vecteurs de  . Pour
. Pour
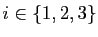 ,
on note
,
on note
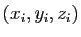 des coordonnées de
des coordonnées de 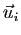 dans la base
dans la base 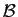 . On appelle
déterminant de
. On appelle
déterminant de
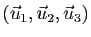 dans
la base
dans
la base 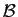 le nombre réel :
le nombre réel :
Pour calculer le déterminant de trois vecteurs,
on peut utiliser la règle de Sarrus:
on réécrit les deux premières lignes du déterminant
en dessous de celui-ci, puis on effectue tous les
produits en diagonale. On affecte du signe 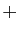 les diagonales
descendantes, du signe
les diagonales
descendantes, du signe  les diagonales montantes, et on ajoute le
tout (figure 2). Par exemple:
les diagonales montantes, et on ajoute le
tout (figure 2). Par exemple:
Figure 2:
Règle de Sarrus.
|
|
Démonstration : Ces assertions se montrent par des calculs élémentaires
comme dans le cas du déterminant de deux vecteurs.
Corollaire 2
Soit
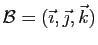 une base de
une base de  .
Pour tout triplet
.
Pour tout triplet
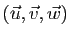 de vecteurs de
de vecteurs de  ,
,
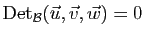 si et seulement si
les vecteurs
si et seulement si
les vecteurs 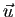 ,
, 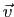 et
et 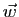 sont coplanaires.
sont coplanaires.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
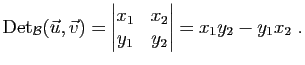
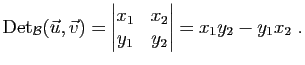
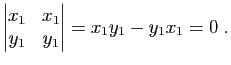
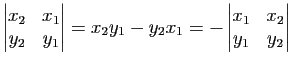
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() et
et ![]() des nombres réels. L'assertion
c) découle des égalités :
des nombres réels. L'assertion
c) découle des égalités :
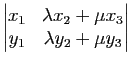
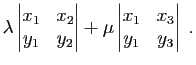
![]() ,
, ![]() (resp.
(resp. ![]() ,
, ![]() )
les coordonnées de
)
les coordonnées de ![]() (resp.
(resp. ![]() )
dans la base
)
dans la base ![]() .
.
![]() et
et ![]() ne sont pas colinéaires,
alors la famille
ne sont pas colinéaires,
alors la famille
![]() est une base
de
est une base
de ![]() . Par la relation d), on obtient que :
. Par la relation d), on obtient que :
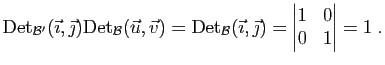
![]() un espace vectoriel de dimension
un espace vectoriel de dimension ![]() (par exemple
(par exemple
![]() ).
Soient
).
Soient ![]() ,
, ![]() et
et ![]() des vecteurs de
des vecteurs de ![]() .
La famille
.
La famille
![]() est liée si et seulement
si les trois vecteurs sont coplanaires, ou encore si et
seulement si un de ces vecteurs
est une combinaison linéaire des deux autres.
est liée si et seulement
si les trois vecteurs sont coplanaires, ou encore si et
seulement si un de ces vecteurs
est une combinaison linéaire des deux autres.
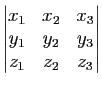
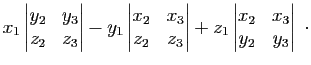
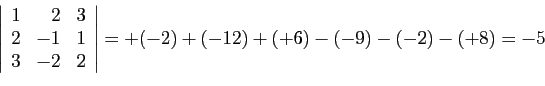
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales