Cette section rappelle les équations des droites et des plans. Nous
commençons par la dimension 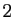 , et considérons un plan affine
, et considérons un plan affine
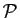 et son plan vectoriel associé
et son plan vectoriel associé 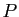 .
.
Soit  un point de
un point de 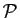 et
et  un vecteur non nul
de
un vecteur non nul
de 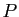 .
La droite de vecteur directeur
.
La droite de vecteur directeur  passant par
passant par  est l'ensemble des points
est l'ensemble des points
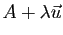 , où
, où 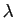 parcourt
parcourt
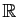 .
.
Supposons le plan muni d'un repère
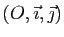 . Notons
. Notons 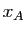 et
et 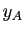 les
coordonnées de
les
coordonnées de  dans le repère
dans le repère
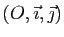 ,
,
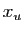 et
et 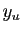 les coordonnées
de
les coordonnées
de  dans la base
dans la base
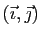 . Les coordonnées
. Les coordonnées 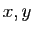 de
de
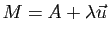 sont :
sont :
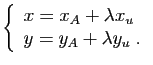 |
(2) |
Les équations ci-dessus sont les équations paramétriques
de la droite 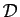 .
On obtient son équation implicite (on dit
aussi «cartésienne»)
en notant que le point
.
On obtient son équation implicite (on dit
aussi «cartésienne»)
en notant que le point 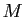 appartient à la droite
appartient à la droite
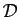 si et seulement si les vecteurs
si et seulement si les vecteurs
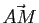 et
et 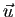 sont colinéaires, ce qui se traduit,
à l'aide du déterminant par l'équation :
sont colinéaires, ce qui se traduit,
à l'aide du déterminant par l'équation :
c'est-à-dire :
La proposition suivante montre que, réciproquement, toute
équation de ce type définit bien une droite.
Démonstration : Sans perte de généralité, nous pouvons supposer 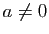 .
Soit
.
Soit  un point dont les coordonnées
un point dont les coordonnées 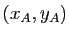 vérifient
(3) (par
exemple
vérifient
(3) (par
exemple 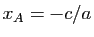 et
et 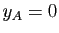 ).
Nous devons démontrer que, pour tout point
).
Nous devons démontrer que, pour tout point 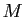 dont les
coordonnées vérifient (3), le vecteur
dont les
coordonnées vérifient (3), le vecteur
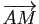 et le vecteur
et le vecteur  de
coordonnées
de
coordonnées 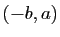 sont colinéaires.
Ecrivons :
sont colinéaires.
Ecrivons :
et soustrayons les deux équations. On obtient:
Les coordonnées du vecteur
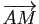 sont
sont
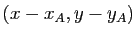 . Posons
. Posons
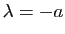 et
et 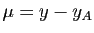 . On vérifie que
. On vérifie que
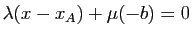
et
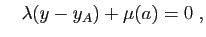
soit
Réciproquement, soit 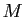 un point tel que
un point tel que
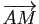 et
et
 sont colinéaires. Soient
sont colinéaires. Soient 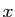 et
et 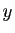 les
coordonnées de
les
coordonnées de 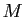 : il existe un réel
: il existe un réel
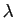 tel que,
tel que,
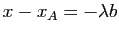
et
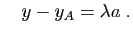
Ceci entraîne:
et donc :

En dimension 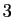 un plan est déterminé par un point
un plan est déterminé par un point  et deux
vecteurs
et deux
vecteurs
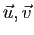 non colinéaires.
non colinéaires.
Soit
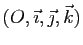 un repère de l'espace. Les trois coordonnées d'un
point du plan
un repère de l'espace. Les trois coordonnées d'un
point du plan 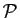 s'écrivent :
s'écrivent :
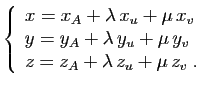 |
(4) |
Ce sont les équations paramétriques du plan 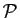 . Pour
obtenir son équation implicite, il faut éliminer
. Pour
obtenir son équation implicite, il faut éliminer 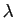 et
et 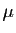 dans les équations paramétriques. C'est moins facile
qu'en dimension
dans les équations paramétriques. C'est moins facile
qu'en dimension 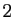 . L'expression des trois coefficients
. L'expression des trois coefficients 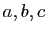 ci-dessous peut paraître arbitraire, mais vous y reconnaîtrez
en fait trois déterminants. Nous expliquerons plus loin leur sens
mathématique.
ci-dessous peut paraître arbitraire, mais vous y reconnaîtrez
en fait trois déterminants. Nous expliquerons plus loin leur sens
mathématique.
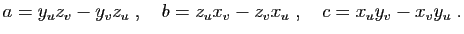 |
(5) |
Démonstration : La vérification, laissée au lecteur, est un peu
fastidieuse, mais elle ne présente aucune difficulté.
Multiplions les équations paramétriques
(4) respectivement par 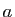 ,
, 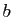 et
et 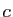 , et ajoutons les
trois: d'après le lemme 1
, et ajoutons les
trois: d'après le lemme 1
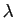 et
et 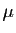 disparaissent et on obtient :
disparaissent et on obtient :
Réciproquement, toute
équation du type
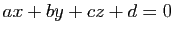 définit bien un plan, que nous
caractériserons à la section suivante.
définit bien un plan, que nous
caractériserons à la section suivante.
En dimension 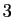 , les équations paramétriques
de la droite
, les équations paramétriques
de la droite
sont sans surprise:
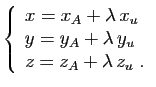 |
(7) |
Pour éliminer 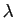 et obtenir des équations implicites,
nous pouvons appliquer la technique déjà utilisée en dimension
et obtenir des équations implicites,
nous pouvons appliquer la technique déjà utilisée en dimension 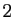 ,
par exemple aux deux premières équations, ensuite aux deux
dernières. Voici le résultat.
,
par exemple aux deux premières équations, ensuite aux deux
dernières. Voici le résultat.
Les deux équations obtenues sont les équations de deux plans dont
la droite 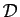 est l'intersection. Evidemment elles n'ont rien
d'uniques. Il existe une infinité de manières d'exprimer une droite
comme intersection de deux plans.
est l'intersection. Evidemment elles n'ont rien
d'uniques. Il existe une infinité de manières d'exprimer une droite
comme intersection de deux plans.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() un point de
un point de ![]() et
et ![]() un vecteur non nul
de
un vecteur non nul
de ![]() .
La droite de vecteur directeur
.
La droite de vecteur directeur ![]() passant par
passant par ![]() est l'ensemble des points
est l'ensemble des points
![]() , où
, où ![]() parcourt
parcourt
![]() .
.
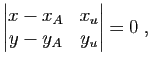
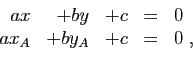
![]() un plan est déterminé par un point
un plan est déterminé par un point ![]() et deux
vecteurs
et deux
vecteurs
![]() non colinéaires.
non colinéaires.
![]() ,
, ![]() et
et ![]() , et ajoutons les
trois: d'après le lemme 1
, et ajoutons les
trois: d'après le lemme 1
![]() et
et ![]() disparaissent et on obtient :
disparaissent et on obtient :
![]() , les équations paramétriques
de la droite
, les équations paramétriques
de la droite
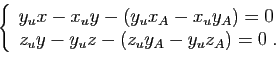
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales