Une fonction  est continue en
est continue en  quand elle admet
quand elle admet
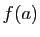 comme limite en
comme limite en  .
.
Définition 5
Soit  un réel et
un réel et  une fonction définie au voisinage de
une fonction définie au voisinage de
 . On dit que
. On dit que  est :
est :
- continue en
 si
si
soit :
- continue à gauche en
 si
si
soit :
- continue à droite en
 si
si
soit :
Par exemple la fonction partie entière
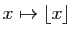 est continue en
est continue en  si
si  n'est pas un entier. Elle est continue à
droite (mais pas à gauche) en
n'est pas un entier. Elle est continue à
droite (mais pas à gauche) en  si
si  est entier : voir figure
2.
est entier : voir figure
2.
On déduit du théorème 1 une
caractérisation de la continuité en termes de suites.
Théorème 9
La fonction  est continue en
est continue en  , si et seulement si pour toute
suite de réels
, si et seulement si pour toute
suite de réels 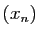 telle que
telle que
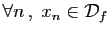 et
convergeant vers
et
convergeant vers  , la suite
, la suite 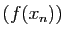 converge vers
converge vers 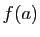 .
.
Observons que si une fonction est continue en un point, elle est
nécessairement définie en ce point. Nous avons vu qu'une fonction
 pouvait admettre une limite en
pouvait admettre une limite en  , sans être définie en
, sans être définie en  .
Si c'est le cas, on appelle prolongement par continuité de
.
Si c'est le cas, on appelle prolongement par continuité de
 en
en  , la fonction
, la fonction
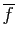 , définie sur
, définie sur
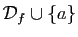 , et telle que
, et telle que
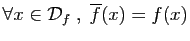
et
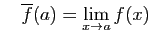
Par exemple,
Cette fonction peut être prolongée par continuité en 0 :
Des théorèmes 2 et
3, on déduit que la somme, le produit, la
composée de deux fonctions continues sont continues.
Théorème 10
Soient  et
et 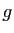 deux fonctions. Soit
deux fonctions. Soit  un réel.
un réel.
- Si
 et
et 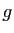 sont continues en
sont continues en  , alors
, alors 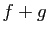 et
et 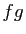 sont
continues en
sont
continues en  .
.
- Si
 est continue en
est continue en  et
et 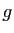 est continue en
est continue en 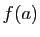 , alors
, alors
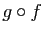 est continue en
est continue en  .
.
Ce théorème permet de démontrer la continuité de toutes les
fonctions que vous aurez à examiner, à condition d'admettre la
continuité des «briques de base» que sont les fonctions usuelles.
Toutes les fonctions usuelles sont continues en tout
point où elles sont définies
Ceci concerne les fonctions puissances, exponentielle, logarithme,
sinus, cosinus, mais exclut bien sûr la partie entière et la
partie décimale.
À titre d'exemple, nous allons le démontrer pour la fonction
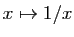 .
.
Proposition 7
La fonction  qui à
qui à  associe
associe 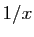 est continue en tout point
de
est continue en tout point
de
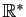 .
.
Démonstration : Soit  un réel non nul. Soit
un réel non nul. Soit
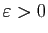 . Notons
. Notons
Si
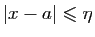 , alors
, alors
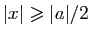 .
Donc :
.
Donc :
Donc,
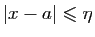 entraîne
entraîne
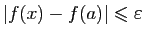 .
. Les fonctions constantes, ainsi que la fonction identité
Les fonctions constantes, ainsi que la fonction identité
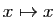 sont évidemment continues en tout point de
sont évidemment continues en tout point de
 .
Du théorème 10, on déduit qu'il
en est de même pour les fonctions polynômes.
En utilisant la proposition
7, on obtient que toute fraction
rationnelle (quotient de deux fonctions
polynômes) est continue en tout point
où son dénominateur ne
s'annule pas.
.
Du théorème 10, on déduit qu'il
en est de même pour les fonctions polynômes.
En utilisant la proposition
7, on obtient que toute fraction
rationnelle (quotient de deux fonctions
polynômes) est continue en tout point
où son dénominateur ne
s'annule pas.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
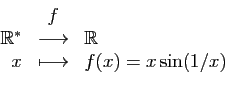
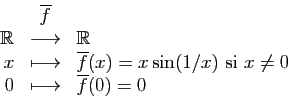
![]() .
.
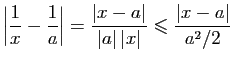
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales