Comme pour les suites, «la monotonie entraîne l'existence de
limites».
Démonstration : Supposons d'abord que  est minorée :
est minorée : ![$ f(]a,b[)$](img158.gif) est une partie
minorée de
est une partie
minorée de
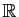 , elle admet donc une borne inférieure finie,
notons-la
, elle admet donc une borne inférieure finie,
notons-la  . Soit
. Soit
 un réel positif fixé. Par
définition de la borne inférieure, il existe
un réel positif fixé. Par
définition de la borne inférieure, il existe ![$ c\in]a,b[$](img159.gif) tel que
tel que
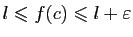 . Mais alors, puisque
. Mais alors, puisque  est croissante,
est croissante,
Donc  admet
admet 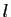 pour limite à droite en
pour limite à droite en  .
Si
.
Si  n'est pas minorée, pour tout
n'est pas minorée, pour tout 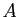 , il existe
, il existe ![$ c\in]a,b[$](img159.gif) , tel
que
, tel
que
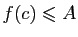 . Puisque
. Puisque  est croissante :
est croissante :
Donc la limite à droite de  en
en  est
est 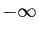 .
.
Pour la limite à gauche en 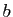 , on procède de manière
analogue, en distinguant le cas où
, on procède de manière
analogue, en distinguant le cas où  est majorée, du cas
où elle ne l'est pas.
est majorée, du cas
où elle ne l'est pas. L'énoncé du théorème 4, reste vrai si
L'énoncé du théorème 4, reste vrai si
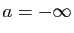 , ou
, ou 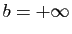 .
Evidemment, le même résultat vaut pour une fonction
décroissante, en inversant le rôle de
.
Evidemment, le même résultat vaut pour une fonction
décroissante, en inversant le rôle de 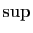 et
et 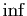 . On
retiendra que
. On
retiendra que
toute fonction monotone sur un intervalle admet une
limite à gauche
et une limite à droite en tout point de cet
intervalle.
La limite à gauche peut très bien ne pas être égale à la
limite à droite. Par exemple, la
fonction «partie entière» est croissante
sur
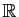 , et pour tout
, et pour tout
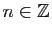 ,
,
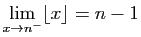
et
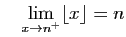
Figure:
Graphe de la fonction partie entière
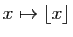 .
.
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() , on procède de manière
analogue, en distinguant le cas où
, on procède de manière
analogue, en distinguant le cas où ![]() est majorée, du cas
où elle ne l'est pas.
est majorée, du cas
où elle ne l'est pas.![]() L'énoncé du théorème 4, reste vrai si
L'énoncé du théorème 4, reste vrai si
![]() , ou
, ou ![]() .
Evidemment, le même résultat vaut pour une fonction
décroissante, en inversant le rôle de
.
Evidemment, le même résultat vaut pour une fonction
décroissante, en inversant le rôle de ![]() et
et ![]() . On
retiendra que
. On
retiendra que
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales