Nous commençons par la convergence en un point, vers une limite
finie. Afin d'éviter les cas pathologiques, nous supposerons
toujours que les fonctions étudiées sont définies au
voisinage du point considéré (cf. définition
2).
Tout intervalle centré en 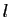 contient toutes les valeurs
contient toutes les valeurs 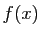 ,
pour
,
pour  suffisamment proche de
suffisamment proche de  .
Observez que
.
Observez que  peut très bien ne pas être
définie en
peut très bien ne pas être
définie en  , et admettre quand même une limite en
, et admettre quand même une limite en  .
Voici un premier exemple (figure 1).
.
Voici un premier exemple (figure 1).
Figure:
Graphe de la fonction
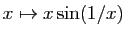 .
.
|
|
Pour tout
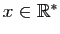 ,
,
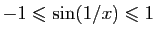 . Donc si
. Donc si
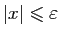 et
et 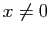 , alors
, alors
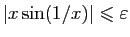 :
:
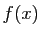 tend vers
0 quand
tend vers
0 quand  tend vers 0.
tend vers 0.
La convergence peut se caractériser en termes de suites.
Théorème 1
Soit  un réel et
un réel et  une fonction définie au voisinage de
une fonction définie au voisinage de  ,
sauf peut-être en
,
sauf peut-être en  , et à valeurs dans
, et à valeurs dans
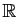 . Soit
. Soit 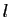 un réel. La fonction
un réel. La fonction  tend vers
tend vers 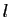 quand
quand  tend vers
tend vers  , si et seulement si, pour toute
suite
, si et seulement si, pour toute
suite 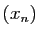 , à valeurs dans
, à valeurs dans
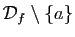 et convergeant vers
et convergeant vers  , la
suite
, la
suite 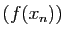 converge vers
converge vers 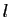 .
.
Démonstration : Montrons d'abord la condition nécessaire : si  tend vers
tend vers 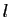 au
sens de la définition 3, alors pour toute
suite
au
sens de la définition 3, alors pour toute
suite 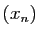 convergeant vers
convergeant vers  , la suite
, la suite 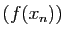 tend vers
tend vers 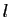 .
.
Soit
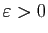 , et
, et 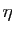 tel que si
tel que si
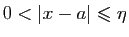 , alors
, alors
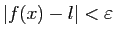 . Soit
. Soit 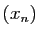 une suite de
une suite de
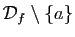 convergeant vers
convergeant vers  . Il existe
. Il existe 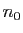 tel que pour tout
tel que pour tout
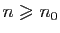 ,
,
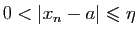 . Mais
. Mais
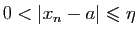 entraîne
entraîne
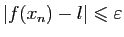 , par
hypothèse. Donc la suite
, par
hypothèse. Donc la suite 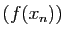 converge vers
converge vers 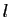 .
.
Voici maintenant la condition suffisante, dont nous allons démontrer
la contraposée : si  ne tend pas vers
ne tend pas vers 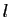 , alors il existe une suite
, alors il existe une suite
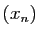 convergeant vers
convergeant vers  telle que la suite
telle que la suite 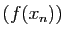 ne tend
pas vers
ne tend
pas vers 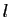 . Ecrivons donc que
. Ecrivons donc que  ne tend pas vers
ne tend pas vers 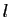 .
.
Posons 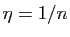 :
:
Notons 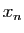 un des réels dont l'existence est affirmée ci-dessus. La
suite
un des réels dont l'existence est affirmée ci-dessus. La
suite 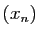 converge vers
converge vers  car
car
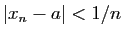 , pourtant la suite
, pourtant la suite
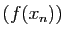 ne tend pas vers
ne tend pas vers 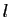 , car
, car
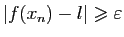 .
. Voici deux conséquences faciles de la définition.
Voici deux conséquences faciles de la définition.
Proposition 1
Soit  une fonction de
une fonction de
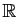 dans
dans
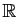 et
et  un réel.
un réel.
- Si
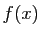 converge quand
converge quand  tend vers
tend vers  , alors la limite est unique.
, alors la limite est unique.
- Si
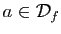 et si
et si
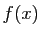 converge vers
converge vers
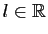 quand
quand  tend vers
tend vers  ,
alors
,
alors  est bornée au voisinage de
est bornée au voisinage de  .
.
Démonstration :
- Supposons que
 vérifie la définition 3
pour deux réels
vérifie la définition 3
pour deux réels 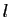 et
et 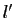 distincts. Posons
distincts. Posons
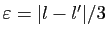 . Alors
les intervalles
. Alors
les intervalles
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) et
et
![$ [l'-\varepsilon ,l'+\varepsilon ]$](img85.gif) sont
disjoints. Pour
sont
disjoints. Pour  suffisamment proche de
suffisamment proche de  ,
le réel
,
le réel 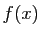 devrait appartenir
aux deux intervalles à la fois : c'est impossible.
devrait appartenir
aux deux intervalles à la fois : c'est impossible.
- Fixons
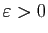 , et
, et 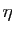 tel que
tel que 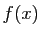 reste dans l'intervalle
reste dans l'intervalle
![$ ]l-\varepsilon ,l+\varepsilon [$](img86.gif) pour tout
pour tout
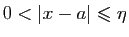 . Alors :
. Alors :
et
Donc  est majorée et minorée au voisinage de
est majorée et minorée au voisinage de  .
.

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
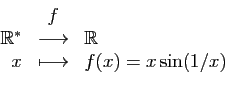
![]() , et
, et ![]() tel que si
tel que si
![]() , alors
, alors
![]() . Soit
. Soit ![]() une suite de
une suite de
![]() convergeant vers
convergeant vers ![]() . Il existe
. Il existe ![]() tel que pour tout
tel que pour tout
![]() ,
,
![]() . Mais
. Mais
![]() entraîne
entraîne
![]() , par
hypothèse. Donc la suite
, par
hypothèse. Donc la suite ![]() converge vers
converge vers ![]() .
.
![]() ne tend pas vers
ne tend pas vers ![]() , alors il existe une suite
, alors il existe une suite
![]() convergeant vers
convergeant vers ![]() telle que la suite
telle que la suite ![]() ne tend
pas vers
ne tend
pas vers ![]() . Ecrivons donc que
. Ecrivons donc que ![]() ne tend pas vers
ne tend pas vers ![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales