La notion de limite se combine avec les opérations
sur les fonctions comme on l'attend. Nous énoncerons les résultats
dans le théorème 2. Ils peuvent se
déduire des résultats analogues sur les suites numériques, via
le théorème 1. Nous conseillons au lecteur de le
vérifier, puis de comparer cette approche
avec les démonstrations directes qui suivent. Elles sont
basées sur le lemme suivant.
Lemme 1
Soit  un réel.
Soient
un réel.
Soient  et
et 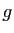 deux fonctions de
deux fonctions de
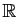 dans
dans
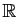 , définies au
voisinage de
, définies au
voisinage de  , sauf peut-être en
, sauf peut-être en  .
.
- Si
alors
- Si
 est bornée au voisinage de
est bornée au voisinage de  et
et
alors
Démonstration :
- Fixons
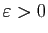 . Soit
. Soit 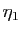 tel que pour
tel que pour
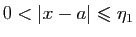 ,
,
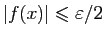 . De même, soit
. De même, soit 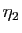 tel que pour
tel que pour
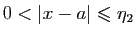 ,
,
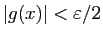 . Alors, pour
. Alors, pour
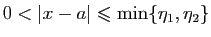 ,
,
d'où le résultat.
- Soit
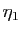 et
et 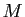 deux réels tels que
deux réels tels que
Fixons
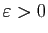 . Soit
. Soit 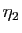 tel que pour
tel que pour
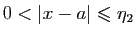 ,
,
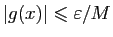 . Alors, pour
. Alors, pour
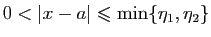 ,
,
d'où le résultat.

Théorème 2
Soit  un réel.
Soient
un réel.
Soient  et
et 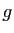 deux fonctions de
deux fonctions de
 dans
dans
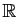 , définies sur
un intervalle ouvert autour de
, définies sur
un intervalle ouvert autour de  .
.
- Si
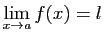
et
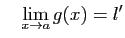
alors
- Si
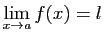
et
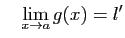
alors
Démonstration : Pour nous ramener au lemme 1,
observons d'abord que 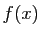 tend vers
tend vers 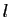 quand
quand  tend
vers
tend
vers  , si et seulement si
, si et seulement si 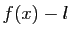 tend vers 0.
tend vers 0.
- Quand
 tend vers
tend vers  ,
, 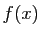 tend vers
tend vers 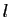 et
et 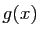 tend vers
tend vers 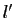 , donc
, donc 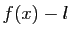 et
et 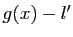 tendent vers 0.
Donc
tendent vers 0.
Donc
tend vers 0 d'après le point 1. du lemme
1. D'où le résultat.
- Nous voulons montrer que
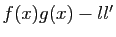 tend vers 0. Ecrivons :
tend vers 0. Ecrivons :
Il suffit de montrer séparément que les deux fonctions
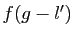 et
et 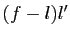 tendent vers 0, d'après le premier
point du lemme 1.
Mais chacune de ces deux fonctions
est le produit d'une fonction convergeant vers 0 par une fonction
bornée au voisinage de 0 (
tendent vers 0, d'après le premier
point du lemme 1.
Mais chacune de ces deux fonctions
est le produit d'une fonction convergeant vers 0 par une fonction
bornée au voisinage de 0 ( est bornée au voisinage de 0
car elle converge). D'où le résultat, par le point 2.
du lemme 1.
est bornée au voisinage de 0
car elle converge). D'où le résultat, par le point 2.
du lemme 1.
 Si une application est constante, sa limite en tout point est égale
à cette constante.
Comme cas particulier du théorème
2, si
Si une application est constante, sa limite en tout point est égale
à cette constante.
Comme cas particulier du théorème
2, si 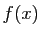 tend vers
tend vers 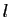 quand
quand  tend vers
tend vers  , et
, et 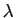 est un réel quelconque, alors
la limite en
est un réel quelconque, alors
la limite en  de
de
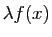 est
est 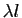 .
.
Le résultat attendu sur la composition des limites se vérifie, à
un détail près.
Démonstration : Soit
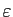 un réel strictement positif. Il existe
un réel strictement positif. Il existe 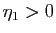 tel que
tel que
Il existe 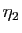 tel que
tel que
Donc :

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
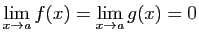
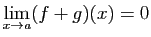
 est bornée au voisinage de
est bornée au voisinage de  et
alors
et
alors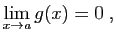
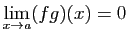
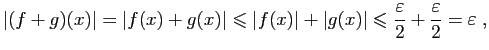
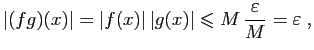
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales