Exercice 1
On appelle médianes d'un triangle non aplati 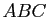 les trois droites
les trois droites 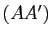 ,
, 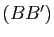 ,
, 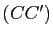 joignant un sommet de ce triangle au milieu du côté opposé.
joignant un sommet de ce triangle au milieu du côté opposé.
- Écrire l'isobarycentre
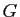 d'un triangle
d'un triangle 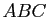 comme barycentre des points
comme barycentre des points  et
et 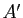 (resp.
(resp.  et
et 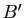 ,
, 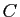 et
et 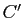 ), où
), où 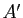 ,
, 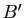 ,
, 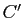 sont les milieux respectifs de
sont les milieux respectifs de ![$ [BC]$](img629.gif) ,
, ![$ [CA]$](img630.gif) ,
, ![$ [AB]$](img271.gif) . Montrer que
. Montrer que
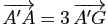 ,
,
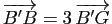 ,
,
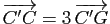 .
.
- En déduire que l'isobarycentre d'un triangle non aplati appartient aux trois médianes de ce triangle, qui sont donc concourantes.
Exercice 2
Soient  et
et  deux points d'un espace affine
deux points d'un espace affine  et
et 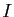 le milieu du segment
le milieu du segment ![$ [AB]$](img271.gif) . Pour tout point
. Pour tout point 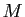 de
de  , on note
, on note 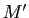 l'isobarycentre des trois points
l'isobarycentre des trois points  ,
,  ,
, 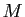 .
.
- Comparer les vecteurs
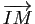 et
et
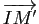 .
.
- En déduire la nature géométrique de l'application de
 dans
dans  qui à tout point
qui à tout point 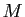 associe le point
associe le point 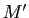 .
.
Exercice 3
Triangle des milieux
Soit 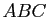 un triangle,
un triangle, 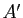 ,
, 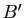 ,
, 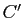 les milieux des segments
les milieux des segments ![$ [BC]$](img629.gif) ,
, ![$ [CA]$](img630.gif) ,
, ![$ [AB]$](img271.gif) ,
, 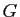 l'isobarycentre des points
l'isobarycentre des points  ,
,  ,
, 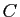 .
.
- Montrer que
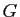 est l'isobarycentre des trois points
est l'isobarycentre des trois points 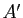 ,
, 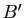 ,
, 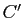 .
.
- En déduire que le triangle
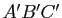 (qu'on appellera triangle des milieux du triangle
(qu'on appellera triangle des milieux du triangle 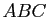 ) est l'image du triangle
) est l'image du triangle  par une homothétie dont on précisera le centre et le rapport.
par une homothétie dont on précisera le centre et le rapport.
- Montrer que
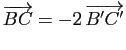 ,
,
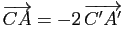 ,
,
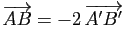 .
.
- Étant donné un triangle
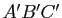 , montrer qu'il existe un triangle
, montrer qu'il existe un triangle 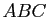 et un seul dont il est le triangle des milieux. Donner, dans le cas où le triangle
et un seul dont il est le triangle des milieux. Donner, dans le cas où le triangle 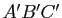 n'est pas aplati, une construction du triangle
n'est pas aplati, une construction du triangle 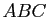 ne faisant intervenir que des tracés de parallèles.
ne faisant intervenir que des tracés de parallèles.
Exercice 4
Quadrilatère des milieux
Soit, dans un plan affine  ,
, 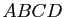 un quadrilatère,
un quadrilatère, 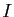 ,
, 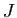 ,
, 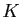 ,
, 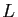 ,
, 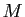 ,
, 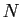 les milieux respectifs des segments
les milieux respectifs des segments ![$ [AB]$](img271.gif) ,
, ![$ [BC]$](img629.gif) ,
, ![$ [CD]$](img643.gif) ,
, ![$ [DA]$](img644.gif) ,
, ![$ [AC]$](img645.gif) ,
, ![$ [BD]$](img646.gif) .
.
- Montrer que les segments
![$ [IK]$](img647.gif) ,
, ![$ [JL]$](img648.gif) et
et ![$ [MN]$](img649.gif) ont tous pour milieu l'isobarycentre des quatre points
ont tous pour milieu l'isobarycentre des quatre points  ,
,  ,
, 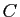 ,
, 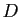 .
.
- En déduire que
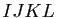 ,
, 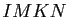 et
et 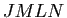 sont des parallélogrammes.
sont des parallélogrammes.
- Retrouver ces résultats en exprimant les vecteurs
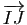 ,
,
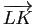 ,
,
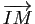 ,
,
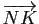 ,
,
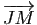 ,
,
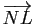 en fonction des vecteurs
en fonction des vecteurs
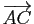 ,
,
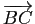 ,
,
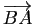 .
.
Exercice 5
Soit dans l'espace 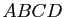 un tétraèdre non aplati. On appelle bimédianes de ce tétraèdre les trois segments joignant les milieux de deux arêtes opposées et médianes les quatre segments
un tétraèdre non aplati. On appelle bimédianes de ce tétraèdre les trois segments joignant les milieux de deux arêtes opposées et médianes les quatre segments ![$ [AA']$](img661.gif) ,
, ![$ [BB']$](img662.gif) ,
, ![$ [CC']$](img663.gif) ,
, ![$ [DD']$](img664.gif) joignant un sommet à l'isobarycentre des trois autres sommets. Montrer que l'isobarycentre
joignant un sommet à l'isobarycentre des trois autres sommets. Montrer que l'isobarycentre 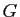 des points
des points  ,
,  ,
, 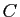 ,
, 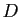 est le milieu des trois bimédianes et qu'il appartient aux quatre médianes. Comparer les vecteurs
est le milieu des trois bimédianes et qu'il appartient aux quatre médianes. Comparer les vecteurs
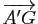 et
et
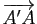 (resp.
(resp.
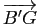 et
et
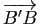 ,
,
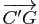 et
et
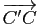 ,
,
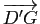 et
et
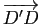 ).
).
Exercice 6
Soit, dans l'espace affine de dimension 3, 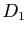 une droite définie par un point
une droite définie par un point  et un vecteur directeur
et un vecteur directeur 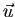 et
et 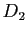 une droite définie par un point
une droite définie par un point  et un vecteur directeur
et un vecteur directeur 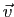 .
Montrer que
.
Montrer que 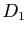 et
et 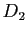 sont coplanaires si et seulement si les trois vecteurs
sont coplanaires si et seulement si les trois vecteurs 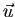 ,
, 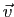 et
et
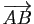 sont liés.
sont liés.
Exercice 7
Soit, dans l'espace affine de dimension 3 rapporté à un repère cartésien, 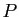 un plan d'équation
un plan d'équation
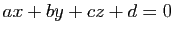 et
et 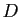 une droite de vecteur directeur
une droite de vecteur directeur
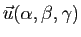 . Donner une condition pour que
. Donner une condition pour que 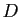 soit parallèle à
soit parallèle à 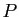 .
.
Exercice 8
L'espace de dimension 3 est rapporté à un repère cartésien. Écrire l'équation du plan passant par le point 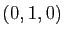 et parallèle au plan d'équation
et parallèle au plan d'équation 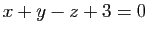 .
.
Exercice 9
Soit, dans l'espace affine de dimension 3 rapporté à un repère cartésien, 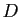 la droite d'équations
la droite d'équations 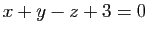 ,
, 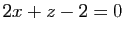 .
Donner l'équation du plan
.
Donner l'équation du plan 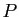 contenant
contenant 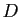 et passant par le point
et passant par le point 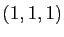 .
.
Exercice 10
Soient 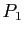 ,
, 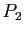 ,
, 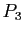 trois plans de l'espace de dimension trois, deux à deux non parallèles. Montrer que les trois droites
trois plans de l'espace de dimension trois, deux à deux non parallèles. Montrer que les trois droites
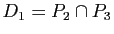 ,
,
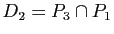 ,
,
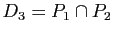 sont parallèles ou concourantes.
sont parallèles ou concourantes.
Exercice 11
Dans l'espace affine de dimension 3 rapporté à un repère cartésien, soit 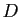 la droite de vecteur directeur
la droite de vecteur directeur 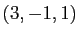 passant par le point de coordonnées
passant par le point de coordonnées 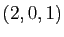 ,
, 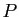 le plan passant par le point
le plan passant par le point 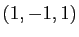 et de vecteurs directeurs
et de vecteurs directeurs 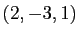 et
et 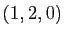 ,
, 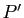 le plan passant par le point
le plan passant par le point 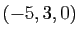 et de vecteurs directeurs
et de vecteurs directeurs 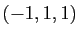 et
et 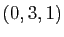 . Déterminer
. Déterminer 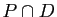 et
et 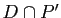 .
.
Exercice 12
- Montrer que trois droites
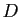 ,
, 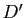 ,
, 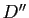 du plan affine, d'équations respectives
du plan affine, d'équations respectives 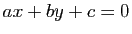 ,
,
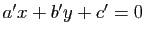 ,
,
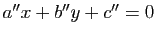 dans un repère cartésien, sont concourantes ou parallèles si et seulement si
dans un repère cartésien, sont concourantes ou parallèles si et seulement si
- En déduire le théorème de Céva : soit
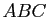 un triangle,
un triangle, 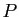 ,
, 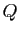 ,
, 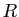 trois points situés respectivement sur les droites
trois points situés respectivement sur les droites 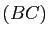 ,
, 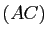 ,
, 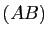 , distincts des sommets de ce triangle ; alors les droites
, distincts des sommets de ce triangle ; alors les droites 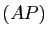 ,
, 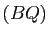 ,
, 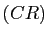 sont concourantes ou parallèles si et seulement si
sont concourantes ou parallèles si et seulement si
Exercice 14
Soient  ,
,  ,
, 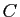 trois points distincts d'une droite affine. Montrer que l'un, et l'un seulement, de ces points appartient au segment défini par les deux autres.
trois points distincts d'une droite affine. Montrer que l'un, et l'un seulement, de ces points appartient au segment défini par les deux autres.
Exercice 16
- Soit
 un espace affine,
un espace affine, 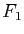 et
et 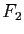 deux sous-espaces affines de
deux sous-espaces affines de  et
et 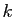 un réel.
Montrer que l'ensemble
un réel.
Montrer que l'ensemble 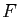 des points
des points
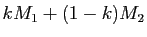 , pour
, pour 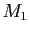 parcourant
parcourant 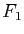 et
et 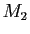 parcourant
parcourant 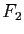 , est un sous-espace affine de
, est un sous-espace affine de  .
.
- Préciser la nature de
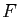 quand
quand 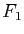 et
et 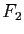 sont deux droites de l'espace affine de dimension 3 (on discutera selon la position de ces droites).
sont deux droites de l'espace affine de dimension 3 (on discutera selon la position de ces droites).
Exercice 17
Montrer que l'enveloppe convexe de trois points  ,
,  ,
, 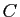 non alignés du plan est la réunion des segments
non alignés du plan est la réunion des segments ![$ [A,M]$](img733.gif) pour
pour 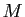 parcourant le segment
parcourant le segment ![$ [B,C]$](img734.gif) . Représenter cette enveloppe convexe sur un dessin.
. Représenter cette enveloppe convexe sur un dessin.
Exercice 18
Soient 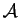 et
et 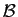 deux parties non vides d'un espace affine
deux parties non vides d'un espace affine  . On appelle jonction de
. On appelle jonction de 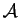 et
et 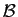 , et on note
, et on note
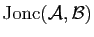 la réunion de tous les segments joignant un point quelconque de
la réunion de tous les segments joignant un point quelconque de 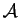 à un point quelconque de
à un point quelconque de 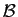 , i. e. l'ensemble des
, i. e. l'ensemble des 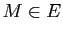 tels qu'il existe
tels qu'il existe
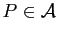 et
et
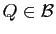 tels que
tels que
![$ M \in [PQ]$](img741.gif) .
.
- Soit
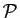 une partie non vide de
une partie non vide de  . Comparer
. Comparer
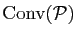 et
et
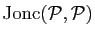 . Dessiner
. Dessiner
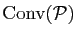 et
et
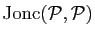 lorsque
lorsque 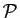 est un ensemble de trois points non alignés.
est un ensemble de trois points non alignés.
- Soit
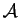 et
et 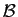 deux convexes d'un espace affine
deux convexes d'un espace affine  . Comparer
. Comparer
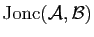 et
et
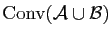 .
.
- Dans
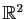 , déterminer
, déterminer
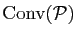 lorsque
lorsque 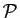 est la réunion de la droite d'équation
est la réunion de la droite d'équation
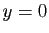 et du point
et du point 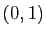 .
.
Exercice 22
Montrer que l'image d'un parallélogramme par une transformation affine est un parallélogramme. L'image par une transformation affine d'un quadrilatère qui n'est pas un parallélogramme peut-elle être un parallélogramme ?
Exercice 23
Soient  et
et 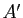 deux points d'un espace affine
deux points d'un espace affine  .
.
- Montrer qu'il existe une unique symétrie centrale qui envoie
 sur
sur 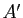 . Déterminer son centre.
. Déterminer son centre.
- Montrer que, pour tout
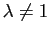 , il existe une unique homothétie de rapport
, il existe une unique homothétie de rapport 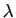 qui envoie
qui envoie  sur
sur 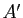 .
Déterminer son centre.
.
Déterminer son centre.
Exercice 24
Soit, dans le plan affine, 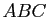 un triangle,
un triangle, 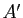 ,
, 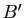 ,
, 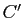 les milieux respectifs de
les milieux respectifs de ![$ [BC]$](img629.gif) ,
, ![$ [CA]$](img630.gif) et
et ![$ [AB]$](img271.gif) ,
, 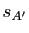 ,
, 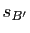 ,
, 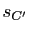 les symétries centrales de centres ces points. Déterminer la nature géométrique des transformations
les symétries centrales de centres ces points. Déterminer la nature géométrique des transformations
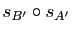 et
et
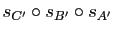 (on pourra déterminer l'image de
(on pourra déterminer l'image de  par ces deux transformations).
par ces deux transformations).
Exercice 25
Déterminer le sous-groupe du groupe affine 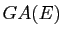 d'un espace affine
d'un espace affine  engendré par les symétries centrales.
engendré par les symétries centrales.
Exercice 26
Soit, dans le plan affine, 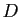 et
et 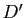 deux droites sécantes en un point
deux droites sécantes en un point  , et
, et 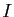 un point n'appartenant à aucune de ces droites. Construire un triangle
un point n'appartenant à aucune de ces droites. Construire un triangle 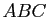 tel que
tel que  appartienne à
appartienne à 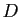 ,
, 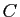 appartienne à
appartienne à 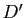 et
et 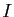 soit le milieu de
soit le milieu de ![$ [BC]$](img629.gif) :
:
- a)
- en considérant les parallèles à
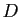 et
et 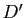 menées par
menées par 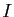 ;
;
- b)
- en considérant la droite symétrique de
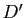 par rapport à
par rapport à 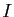 .
.
Exercice 27
Conjuguée d'une translation
- Soit
 un espace affine,
un espace affine, 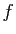 une transformation affine de
une transformation affine de  et
et 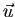 un vecteur de
un vecteur de
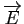 . Montrer que
. Montrer que
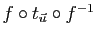 est la translation de vecteur
est la translation de vecteur
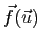 .
.
- En déduire que le centre du groupe affine est réduit à l'identité.
Exercice 29
Soit 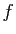 une transformation affine d'un espace affine
une transformation affine d'un espace affine  dont la partie linéaire
dont la partie linéaire 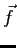 est une homothétie vectorielle de rapport
est une homothétie vectorielle de rapport
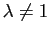 .
.
- Soit
 un point quelconque de
un point quelconque de  . Montrer que le barycentre
. Montrer que le barycentre 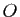 du système de points pondérés
du système de points pondérés
![$ [(A,\lambda),(f(A),-1)]$](img765.gif) est fixe par
est fixe par 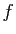 .
.
- En déduire (sans utiliser la proposition 35) que
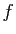 est l'homothétie affine de centre
est l'homothétie affine de centre 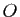 et de rapport
et de rapport 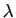 .
.
Exercice 30
- Déterminer les droites globalement invariantes par une translation de vecteur non nul (resp. par une homothétie de rapport différent de
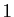 ).
).
- En déduire que la composée de deux homothéties de centres
distincts
 et
et  est
est
- soit une translation de vecteur proportionnel à
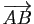 ;
;
- soit une homothétie dont le centre appartient à la droite
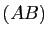 .
.
Exercice 32
Soit, dans le plan affine,
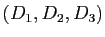 et
et
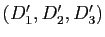 deux triplets constitués chacun de trois droites distinctes concourantes en un point
deux triplets constitués chacun de trois droites distinctes concourantes en un point 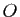 (resp.
(resp. 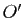 ). Le but de l'exercice est de montrer qu'il existe une transformation affine du plan transformant le premier triplet en le second.
). Le but de l'exercice est de montrer qu'il existe une transformation affine du plan transformant le premier triplet en le second.
- Soit
 (resp.
(resp. 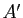 ) un point de
) un point de 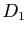 (resp.
(resp. 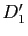 ) distinct de
) distinct de 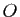 (resp.
(resp. 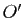 ),
),  (resp.
(resp. 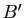 ) son projeté sur
) son projeté sur 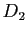 (resp.
(resp. 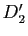 ) dans la direction de
) dans la direction de 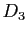 (resp.
(resp. 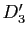 ),
), 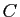 (resp.
(resp. 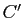 ) son projeté sur
) son projeté sur 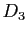 (resp.
(resp. 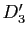 ) dans la direction de
) dans la direction de 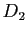 (resp.
(resp. 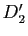 ).
Montrer que
).
Montrer que
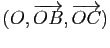 (resp.
(resp.
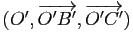 ) est un repère cartésien du plan. Donner les coordonnées du point
) est un repère cartésien du plan. Donner les coordonnées du point  (resp.
(resp. 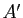 ) dans ce repère.
) dans ce repère.
- En déduire qu'il existe une transformation affine
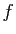 et une seule du plan vérifiant
et une seule du plan vérifiant 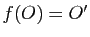 ,
, 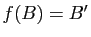 ,
, 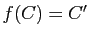 ,
, 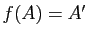 .
.
- Montrer que
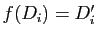 pour
pour 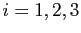 .
.
- Si
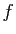 et
et 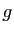 sont deux transformations affines du plan vérifiant
sont deux transformations affines du plan vérifiant
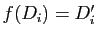 et
et
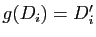 pour
pour 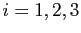 , montrer que
, montrer que
 est une homothétie de centre
est une homothétie de centre 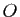 (on pourra considérer les images des points
(on pourra considérer les images des points 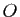 ,
,  ,
,  ,
, 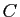 par
par 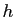 ).
).
Exercice 33
Soit
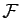 une partie d'un espace affine possédant deux centres de symétrie distincts
une partie d'un espace affine possédant deux centres de symétrie distincts  et
et  .
.
- Montrer qu'il existe une translation de vecteur non nul laissant
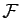 globalement invariante, puis qu'il existe une infinité de telles translations.
globalement invariante, puis qu'il existe une infinité de telles translations.
- En déduire que
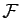 ne peut être bornée.
ne peut être bornée.
- Montrer que
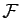 possède une infinité de centres de symétrie.
possède une infinité de centres de symétrie.
Exercice 34
Soit 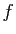 une application affine d'un espace affine
une application affine d'un espace affine  dans lui-même et
dans lui-même et
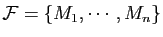 un ensemble fini de points de
un ensemble fini de points de  .
On suppose que
.
On suppose que
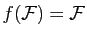 . Montrer que
. Montrer que 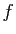 admet au moins un point fixe.
admet au moins un point fixe.
Exercice 35
Soit 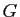 un sous-groupe fini de
un sous-groupe fini de 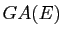 . Montrer qu'il existe au
moins un point de
. Montrer qu'il existe au
moins un point de  qui est fixe par tout élément de
qui est fixe par tout élément de 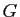 . (On pourra considérer l'isobarycentre de la famille
. (On pourra considérer l'isobarycentre de la famille 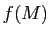 où
où 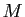 est un point de
est un point de  et
et 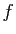 parcourt
parcourt 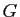 .)
.)
Exercice 37
Un cas particulier du théorème de Desargues
Montrer que deux triangles non aplatis du plan affine se déduisent l'un de l'autre par une homothétie ou une translation si et seulement si leurs côtés sont deux à deux parallèles.
On verra en compléments (section 3.4) le théorème de Desargues dans toute sa généralité.
Exercice 39
Deux cas particuliers du théorème de Pappus
- Soient
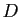 et
et 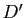 deux droites parallèles du plan affine,
deux droites parallèles du plan affine,  ,
,  ,
, 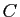 trois points de
trois points de 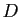 ,
, 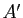 ,
, 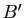 ,
, 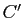 trois points de
trois points de 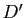 . On suppose
. On suppose 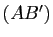 et
et 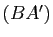 parallèles, ainsi que
parallèles, ainsi que 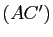 et
et 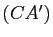 . Montrer que
. Montrer que 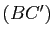 et
et 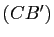 sont parallèles. (On pourra comparer les vecteurs
sont parallèles. (On pourra comparer les vecteurs
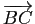 et
et
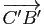 .)
.)
- Même question en supposant les droites
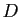 et
et 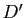 sécantes en un point
sécantes en un point 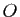 (distinct des points
(distinct des points  ,
,  ,
, 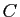 ,
, 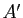 ,
, 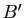 ,
, 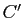 ). (On pourra utiliser le théorème de Thalès.)
). (On pourra utiliser le théorème de Thalès.)
Exercice 45
Soit, dans le plan affine  ,
, 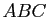 un triangle non aplati,
un triangle non aplati, 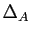 ,
, 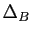 ,
, 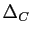 les médianes de ce triangle issues de
les médianes de ce triangle issues de  ,
,  et
et 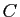 . On note
. On note
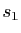 la symétrie par rapport à
la symétrie par rapport à 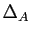 dans la direction de
dans la direction de 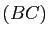
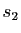 la symétrie par rapport à
la symétrie par rapport à 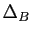 dans la direction de
dans la direction de 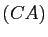
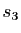 la symétrie par rapport à
la symétrie par rapport à 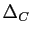 dans la direction de
dans la direction de 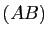
-
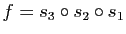 la composée de ces trois symétries.
la composée de ces trois symétries.
- Déterminer les images par
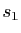 ,
, 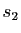 ,
, 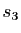 et
et 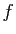 des points
des points  ,
,  ,
, 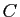 .
.
- En déduire la nature géométrique de
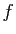 .
.
Exercice 46
Soit, dans un plan affine  rapporté à un repère cartésien
rapporté à un repère cartésien
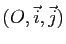 ,
, 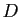 la droite d'équation
la droite d'équation 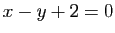 et
et 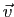 le vecteur de composantes
le vecteur de composantes  . Exprimer les coordonnées
. Exprimer les coordonnées 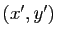 du projeté
du projeté 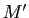 d'un point
d'un point 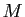 de
de  sur la droite
sur la droite 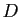 dans la direction du vecteur
dans la direction du vecteur 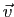 en fonction des coordonnées
en fonction des coordonnées 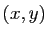 de
de 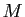 .
.
Exercice 47
Le plan affine est rapporté à un repère cartésien. Déterminer la nature géométrique des applications affines données en coordonnées par les formules :
-
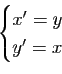
-
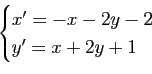
-
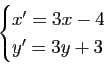
Exercice 48
Le plan affine est rapporté à un repère cartésien
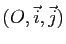 . Donner l'expression en coordonnées des applications affines suivantes :
. Donner l'expression en coordonnées des applications affines suivantes :
- la symétrie centrale de centre
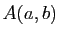 ;
;
- la symétrie par rapport à la droite d'équation
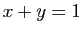 , dans la direction du vecteur
, dans la direction du vecteur 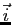 ;
;
- l'affinité de base la droite d'équation
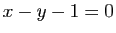 , de direction
, de direction 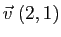 et de rapport
et de rapport 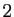 .
.
Exercice 49
Soit, dans l'espace affine  de dimension 3 rapporté à un repère cartésien
de dimension 3 rapporté à un repère cartésien
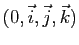 ,
, 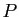 le plan d'équation
le plan d'équation
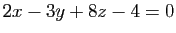 et
et
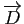 la droite vectorielle de vecteur directeur
la droite vectorielle de vecteur directeur
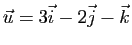 . Donner l'expression en coordonnées de la projection sur
. Donner l'expression en coordonnées de la projection sur 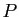 dans la direction
dans la direction
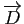 , puis, pour tout réel
, puis, pour tout réel 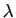 , de l'affinité de base
, de l'affinité de base 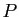 , de direction
, de direction
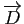 et de rapport
et de rapport 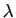 .
.
Exercice 50
Soit 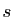 une application affine d'un espace affine
une application affine d'un espace affine  dans lui-même vérifiant
dans lui-même vérifiant
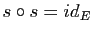 .
.
- Montrer que
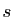 est bijective.
est bijective.
- Montrer que pour tout point
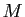 de
de  , le milieu du segment
, le milieu du segment ![$ [Ms(M)]$](img857.gif) est fixe par
est fixe par 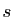 .
.
- Montrer que la partie linéaire
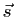 de
de 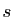 est une symétrie vectorielle de
est une symétrie vectorielle de
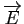 .
.
- Conclure que
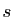 est une symétrie affine de
est une symétrie affine de  .
.
- Montrer par un contre-exemple qu'une transformation affine de
 dont la partie linéaire est une symétrie vectorielle de
dont la partie linéaire est une symétrie vectorielle de
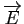 n'est pas nécessairement une symétrie affine.
n'est pas nécessairement une symétrie affine.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
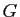 d'un triangle
d'un triangle 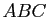 comme barycentre des points
comme barycentre des points  et
et 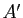 (resp.
(resp.  et
et 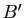 ,
, 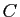 et
et 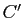 ), où
), où 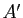 ,
, 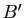 ,
, 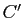 sont les milieux respectifs de
sont les milieux respectifs de ![$ [BC]$](img629.gif) ,
, ![$ [CA]$](img630.gif) ,
, ![$ [AB]$](img271.gif) . Montrer que
. Montrer que
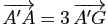 ,
,
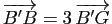 ,
,
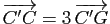 .
.
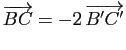
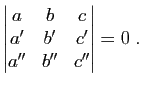
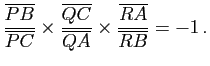
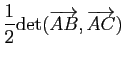
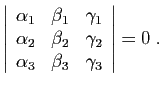
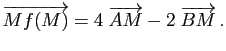
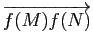
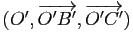
![\includegraphics[width=0.6\textwidth]{figures/trapeze}](img786.gif)
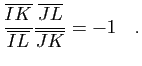
![\includegraphics[width=0.45\textwidth]{figures/desargues1}](img796.gif)
![\includegraphics[width=0.45\textwidth]{figures/desargues2}](img797.gif)
![\includegraphics[width=0.6\textwidth]{figures/desargues3}](img799.gif)
![\includegraphics[width=0.45\textwidth]{figures/pappus1}](img800.gif)
![\includegraphics[width=0.45\textwidth]{figures/pappus2}](img801.gif)
![\includegraphics[width=0.8\textwidth]{figures/tourniquet_triangle}](img811.gif)
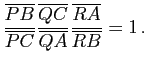
![\includegraphics[width=0.6\textwidth]{figures/menelaus}](img815.gif)
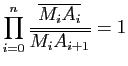
![\includegraphics[width=0.45\textwidth]{figures/ceva}](img823.gif)
![\includegraphics[width=0.45\textwidth]{figures/ceva2}](img824.gif)
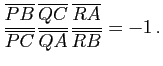
![\includegraphics[width=0.6\textwidth]{figures/triangles}](img826.gif)
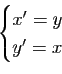
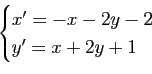
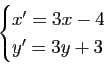
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales