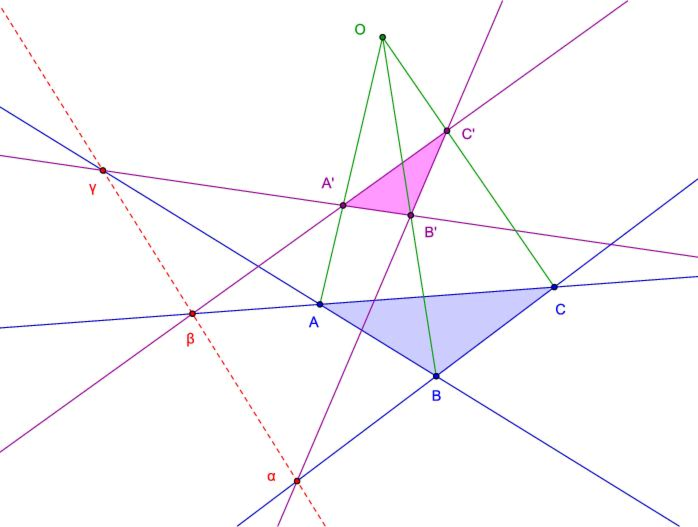
Desargues dans le plan et dans l'espace
Le théorème de Desargues peut s'énoncer dans le plan affine sous la forme suivante :
Théorème 5
Soient 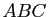 et
et 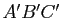 deux triangles non aplatis d'un même plan affine. On suppose
deux triangles non aplatis d'un même plan affine. On suppose  et
et 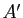 (resp.
(resp. 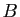 et
et 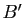 , resp.
, resp. 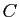 et
et 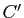 ) distincts. Alors les droites
) distincts. Alors les droites 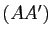 ,
, 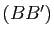 et
et 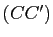 sont concourantes ou parallèles si et seulement si l'une des conditions suivantes est satisfaite :
sont concourantes ou parallèles si et seulement si l'une des conditions suivantes est satisfaite :
- les trois couples de droites
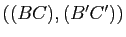 ,
,
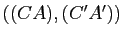 et
et
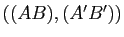 sont constitués de droites sécantes en des points
sont constitués de droites sécantes en des points 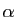 ,
, 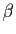 ,
, 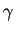 et les trois points
et les trois points 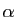 ,
, 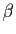 ,
, 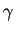 sont alignés (figure 7) ;
sont alignés (figure 7) ;
- les trois couples de droites
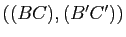 ,
,
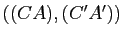 et
et
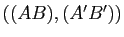 sont constitués de droites parallèles ;
sont constitués de droites parallèles ;
- l'un des trois couples de droites
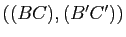 ,
,
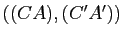 et
et
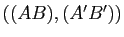 est constitué de droites parallèles, les deux autres de droites sécantes et la droite joignant les deux points d'intersection définis par ces couples est parallèle à la direction commune des droites du premier couple.
est constitué de droites parallèles, les deux autres de droites sécantes et la droite joignant les deux points d'intersection définis par ces couples est parallèle à la direction commune des droites du premier couple.
Les triangles 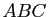 et
et 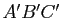 sont alors dits homologiques.
sont alors dits homologiques.
Figure 7:
Le théorème de Desargues
|
|
On a étudié le cas particulier où les trois couples considérés sont constitués de droites parallèles à l'exercice 37 .
Le cas général peut également s'étudier avec les théorèmes classiques de la géométrie plane, mais une façon plus agréable de procéder est de considérer la figure 7 comme une projection plane d'une figure de l'espace.
Considérons pour cela, dans l'espace affine de dimension 3, un tétraèdre 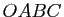 , et un plan
, et un plan 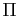 ne passant pas par
ne passant pas par 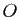 coupant les trois droites
coupant les trois droites 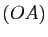 ,
, 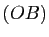 et
et 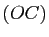 en
en 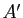 ,
, 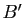 et
et 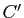 distincts de
distincts de  ,
, 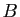 ,
, 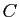 . Les droites
. Les droites 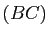 et
et 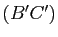 (resp.
(resp. 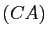 et
et 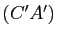 ,
, 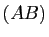 et
et 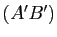 ) sont coplanaires. Supposons-les sécantes en des points
) sont coplanaires. Supposons-les sécantes en des points 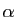 ,
, 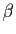 et
et 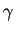 (le cas de droites parallèles se traiterait de manière analogue). Les trois points
(le cas de droites parallèles se traiterait de manière analogue). Les trois points  ,
, 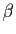 et
et 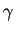 sont alors alignés.
En effet, les plans
sont alors alignés.
En effet, les plans 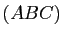 et
et 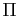 se coupent suivant une droite
se coupent suivant une droite 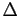 et les points
et les points 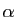 ,
, 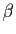 et
et 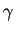 appartiennent tous trois à
appartiennent tous trois à 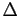 .
.
La figure GeoGebra permet de déplacer les points 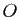 ,
,  ,
, 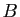 ,
, 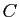 librement et de déplacer les points
librement et de déplacer les points 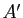 ,
, 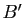 ,
, 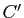 sur les segments
sur les segments ![$ [OA]$](img1045.gif) ,
, ![$ [OB]$](img1046.gif) et
et ![$ [OC]$](img1047.gif) .
.
Pour obtenir la partie directe du théorème de Desargues dans le plan, il suffit alors de considérer la figure plane 7 comme la projection sur le plan d'une figure de l'espace.
En fait, cette démonstration traduit le fait que le théorème de Desargues est fondamentalement un théorème de géométrie projective. Dans un plan projectif, deux droites distinctes se coupent toujours en un point et un seul (des droites parallèles dans le plan affine se coupent en un point à l'infini) et l'énoncé du théorème prend alors la forme beaucoup plus simple suivante :
Théorème 6
Soient 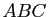 et
et 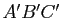 deux triangles non aplatis d'un même plan projectif. On suppose
deux triangles non aplatis d'un même plan projectif. On suppose  et
et 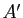 (resp.
(resp. 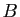 et
et 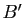 , resp.
, resp. 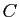 et
et 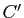 ) distincts et les droites
) distincts et les droites 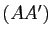 ,
, 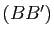 et
et 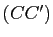 distinctes. Alors les droites
distinctes. Alors les droites 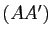 ,
, 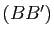 et
et 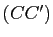 sont concourantes ou parallèles si et seulement si les points d'intersection des trois couples de droites
sont concourantes ou parallèles si et seulement si les points d'intersection des trois couples de droites
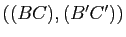 ,
,
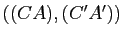 et
et
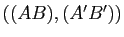 sont alignés.
sont alignés.
Girard Desargues (1591-1661) était un mathématicien et architecte lyonnais. C'est à lui que revient le mérite d'avoir développé pour la première fois d'une manière cohérente la géométrie projective en étudiant la perspective centrale (Exemple de l'une des manières universelles du S.G.D.L. touchant la pratique de la perspective sans employer aucun tiers point, de distance ny d'autre nature, qui soit hors du champ de l'ouvrage, 1636) et les sections planes des cônes de révolution (Brouillon Project d'une Atteinte aux Evènemens des Rencontres du Cone avec un Plan, par L.S.G.D.L., paru à Paris en 1639, avec Privilège).
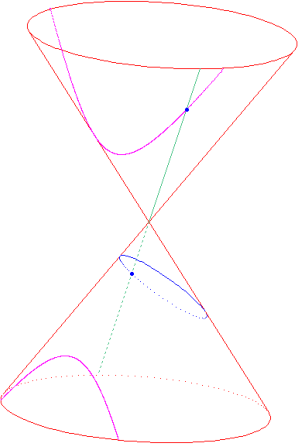
Si la définition des coniques comme sections planes d'un cône ou d'un cylindre de révolution était en effet connue depuis l'antiquité (les Coniques, d'Apollonius de Perge (v.262-v.190 av. J.-C.), qui leur a donné leurs noms), il lui revient l'idée que cette définition permet de mettre en correspondance point par point une ellipse et une hyperbole : si on considère les sections d'un même cône par deux plans (figure 8), toute génératrice de ce cône coupe chacune de ces sections en un point et un seul (à l'exception peut-être d'une ou deux d'entre elles) et il suffit d'associer à tout point de la première section le point correspondant de la seconde.
Figure 8:
Sections planes d'un cône de révolution.
|
|
Ainsi, d'un point de vue projectif, toutes les coniques sont les mêmes.
Les conséquences en sont importantes, puisque certains théorèmes démontrés par exemple pour le cercle (ceux qui ne font intervenir que des propriétés de concours ou d'incidence) restent vrais pour toutes les coniques. C'est ainsi qu'il suffit de démontrer le théorème de Pascal (voir l'hexagramme mystique, dans le chapitre sur les coniques) pour un cercle, le résultat s'en déduisant pour toutes les autres coniques.
Pour définir le plan projectif, il ajoutait au plan ordinaire des points à l'infini, si bien que deux droites distinctes se coupaient toujours en un point et un seul (deux droites parallèles se coupant en un point à l'infini, comme leurs images dans une perspective centrale se coupent en le point de fuite de leur direction).
Il était connu et apprécié des plus grands mathématiciens de son époque (Descartes, Pascal, Fermat), mais son  uvre, rédigée le plus souvent sous forme de brouillons, qu'il signait S.G.D.L. (le Sieur Girard Desargues, Lyonnais), dans un style jugé parfois obscur par ses contemporains, n'a pas connu la postérité qu'elle méritait.
uvre, rédigée le plus souvent sous forme de brouillons, qu'il signait S.G.D.L. (le Sieur Girard Desargues, Lyonnais), dans un style jugé parfois obscur par ses contemporains, n'a pas connu la postérité qu'elle méritait.
Il est l'auteur de deux autres «Brouillons Projects» : l'un concernant la coupe des pierres, l'autre la gnomonique (l'art de construire les cadrans solaires). Il faut remarquer que, d'un point de vue mathématique, un cadran solaire fournit un autre exemple de projection centrale : c'est dans ce cas la pointe du style (la tige dont l'ombre indique l'heure en se déplaçant) qui joue le rôle de l'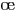 il de l'observateur, le plan de projection étant celui du cadran et l'objet le soleil.
il de l'observateur, le plan de projection étant celui du cadran et l'objet le soleil.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
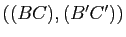 ,
,
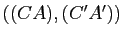 et
et
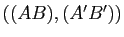 sont constitués de droites sécantes en des points
sont constitués de droites sécantes en des points 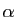 ,
, 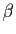 ,
, 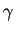 et les trois points
et les trois points  ,
, 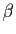 ,
, 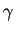 sont alignés (figure 7) ;
sont alignés (figure 7) ;
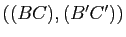 ,
,
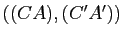 et
et
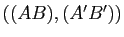 sont constitués de droites parallèles ;
sont constitués de droites parallèles ;
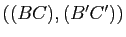 ,
,
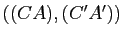 et
et
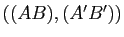 est constitué de droites parallèles, les deux autres de droites sécantes et la droite joignant les deux points d'intersection définis par ces couples est parallèle à la direction commune des droites du premier couple.
est constitué de droites parallèles, les deux autres de droites sécantes et la droite joignant les deux points d'intersection définis par ces couples est parallèle à la direction commune des droites du premier couple.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales