 Pour tout vecteur
Pour tout vecteur 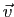 de
de
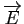 , il existe un couple
, il existe un couple 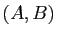 de points de
de points de  et un seul tel que
et un seul tel que
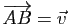 .
.
-
 Pour tout vecteur
Pour tout vecteur 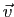 de
de  , il existe un couple
, il existe un couple 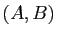 de points de
de points de  tel que
tel que
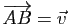 .
.
-
 Pour tout point
Pour tout point  de
de  et tout vecteur
et tout vecteur 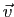 de
de
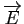 , il existe un point
, il existe un point  de
de  et un seul tel que
et un seul tel que
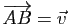 .
.
-
 Pour tout couple
Pour tout couple 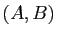 de points de
de points de  , il existe un unique vecteur
, il existe un unique vecteur 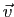 de
de
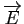 tel que
tel que
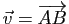 .
.
 Pour tout triplet
Pour tout triplet 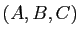 de points de
de points de  , on a
, on a
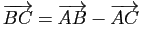 .
.
-
 Pour tout point
Pour tout point  de
de  et tout vecteur
et tout vecteur 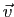 de
de
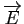 , il existe un unique point
, il existe un unique point  de
de  tel que
tel que
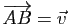 .
.
 Pour tout couple
Pour tout couple 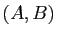 de points de
de points de  , il existe un unique point
, il existe un unique point 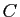 de
de  tel que
tel que
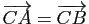 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales