-
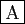
-
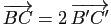 .
.
-
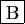
- Les droites
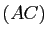 et
et 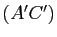 sont parallèles.
sont parallèles.
-
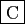
- Il existe une homothétie de rapport 1/2 transformant le triangle
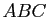 en le triangle
en le triangle 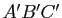 .
.
-
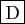
- Les segments
![$ [A'B']$](img864.gif) et
et ![$ [CC']$](img663.gif) ont même milieu.
ont même milieu.
-
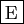
- Les segments
![$ [AA']$](img661.gif) et
et ![$ [BB']$](img662.gif) ont même milieu.
ont même milieu.
![% latex2html id marker 22176
\includegraphics[width=0.9\textwidth]{figures/QCM}](img890.gif)
Il existe une transformation affine du plan transformant le carré ![]() en :
en :
![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales