Soient
![]() des chemin de classe
des chemin de classe
![]() par
morceaux dans
par
morceaux dans
![]() d'image respectives
d'image respectives
![]() et
et
![]() . On définit la chaîne
. On définit la chaîne
![]() comme la somme formelle
comme la somme formelle
![]() et on pose pour toute fonction
et on pose pour toute fonction
![]() continue sur
continue sur ![]()
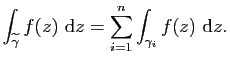
Si chacun des ![]() est fermé, on dit que
est fermé, on dit que
![]() est un
cycle.
est un
cycle.
Notons qu'une chaîne peut être représentée de plusieurs manières comme somme de chemins :
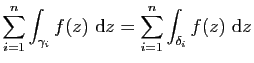
Si
![]() est un cycle et si
est un cycle et si
![]() , on définit
l'indice de
, on définit
l'indice de
![]() par rapport à
par rapport à ![]() par
par
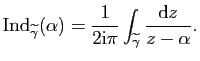
Si dans la définition de
![]() on remplace chacun des chemins
on remplace chacun des chemins
![]() par le chemin opposé on obtient une nouvelle chaîne notée
par le chemin opposé on obtient une nouvelle chaîne notée
![]() et on a
et on a
![]() pour toute fonction
pour toute fonction ![]() continue sur
continue sur ![]() et en
particulier
et en
particulier
![]() .
.
De plus si
![]() et
et
![]() sont deux chaînes on définit de
manière naturelle
sont deux chaînes on définit de
manière naturelle
![]() par
par
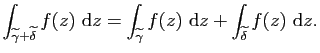
Nous sommes maintenant en mesure d'énoncer le Théorème de Cauchy sous sa forme globale :
Nous allons donner les grandes lignes de la démonstration. Nous n'utiliserons pas la théorie des intégrales dépendant d'un paramètre holomorphe étudiée dans la section 1.3 et qui s'appuyait sur les inégalités de Cauchy, nous démontrerons les résultats liés à cette théorie si nécessaire en utilisant le théorème de Morera.
Démonstration : La fonction ![]() définie sur
définie sur ![]() par
par
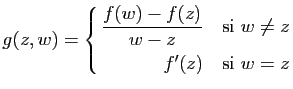 |
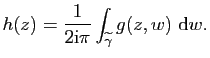
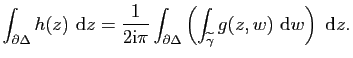
De plus
![]() .
.
Notons
![]() . On pose
. On pose
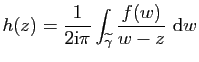
Comme ![]() contient
contient
![]() , on définit une fonction
, on définit une fonction
![]() holomorphe sur
holomorphe sur
![]() en posant
en posant
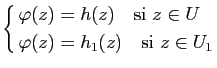 |
D'après les propriétés de l'indice, ![]() contient la composante
connexe non bornée du complémentaire de
contient la composante
connexe non bornée du complémentaire de ![]() , donc
, donc
![]() et en
appliquant le Théorème de Liouville à
et en
appliquant le Théorème de Liouville à ![]() on obtient
on obtient
![]() pour tout
pour tout
![]() , d'où
, d'où ![]() et (i) est
démontré.
et (i) est
démontré.
On déduit (ii) de (i) de la manière suivante : choisissons
![]() et posons
et posons
![]() , alors
, alors
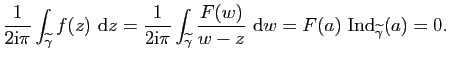
Finalement pour prouver (iii), il suffit d'appliquer (ii) au cycle
![]() .
.![]()
Exemple.
1- Soit ![]() un ouvert convexe ou étoilé,
un ouvert convexe ou étoilé, ![]() un chemin fermé de
classe
un chemin fermé de
classe
![]() par morceaux dans
par morceaux dans ![]() et
et
![]() . La
fonction
. La
fonction
![]() est holomorphe dans
est holomorphe dans ![]() et
d'après le Théorème de Cauchy pour un ouvert convexe ou étoilé
et
d'après le Théorème de Cauchy pour un ouvert convexe ou étoilé
![]() . L'hypothèse du
Théorème 21 est donc satisfaite pour tout cycle
lorsque
. L'hypothèse du
Théorème 21 est donc satisfaite pour tout cycle
lorsque ![]() est convexe ou étoilé.
est convexe ou étoilé.
2- Un compact ![]() de
de ![]() d'intérieur non vide et tel que
d'intérieur non vide et tel que
![]() est un compact à bord si sa
frontière est formée par les images
est un compact à bord si sa
frontière est formée par les images
![]() d'un
nombre fini de chemins
d'un
nombre fini de chemins
![]() , chaque
, chaque
![]() étant un chemin fermé de classe
étant un chemin fermé de classe
![]() par
morceaux sans point stationnaire (i.e. pour tout
par
morceaux sans point stationnaire (i.e. pour tout
![]() en
lequel
en
lequel ![]() est dérivable
est dérivable
![]() ) et sans point
double (i.e. si
) et sans point
double (i.e. si
![]() vérifie
vérifie
![]() alors
alors
![]() ) et les images des
) et les images des ![]() étant
deux à deux disjointes. L'orientation des chemins
étant
deux à deux disjointes. L'orientation des chemins ![]() ,
,
![]() , de telle sorte que lorsque l'on se déplace sur
, de telle sorte que lorsque l'on se déplace sur
![]() dans le sens de l'orientation le compact
dans le sens de l'orientation le compact ![]() se situe à
gauche de
se situe à
gauche de ![]() .
.
Le bord orienté
![]() d'un compact à bord
d'un compact à bord ![]() est un cycle tel
que
est un cycle tel
que
![]() si
si
![]() et
et
![]() si
si
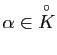 .
Si
.
Si
![]() désignent les composantes connexes de
désignent les composantes connexes de
![]() , le cycle
, le cycle
![]() s'écrit
s'écrit
![]() , où les chemins
, où les chemins
![]() désignent respectivement les bords des composantes
connexes
désignent respectivement les bords des composantes
connexes ![]() . On suppose que
. On suppose que ![]() désigne la composante connexe
non bornée de
désigne la composante connexe
non bornée de
![]() . Si
. Si
![]() ,
,
![]() pour tout
pour tout
![]() . Si
. Si
![]() ,
,
![]()
Soit
![]() une suite de nompbres complexes indexée par
une suite de nompbres complexes indexée par
![]() .
.
Le série entière
![]() converge dans un
disque de rayon
converge dans un
disque de rayon
![]() ,
,
![]() . La série
. La série
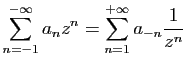
Si ![]() , la série de fonctions
, la série de fonctions
![]() converge
absolument dans la couronne
converge
absolument dans la couronne
![]() et normalement
sur tout compact de cette couronne. Cette série de fonction
s'appelle la série de Laurent associée à la suite
et normalement
sur tout compact de cette couronne. Cette série de fonction
s'appelle la série de Laurent associée à la suite
![]() .
.
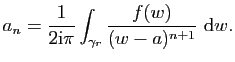
Démonstration : Soient
![]() ,
, ![]() et
et ![]() des réels tels que
des réels tels que
![]() et
et ![]() une fonction holomorphe dans la
couronne
une fonction holomorphe dans la
couronne
![]() . Si
. Si
![]() , on
considère la couronne compacte
, on
considère la couronne compacte
![]() ,
c'est un compact à bord dont le cycle constitué par son bord est
noté
,
c'est un compact à bord dont le cycle constitué par son bord est
noté
![]() . Pour tout
. Pour tout
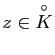 , on a
, on a
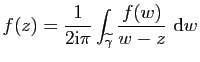
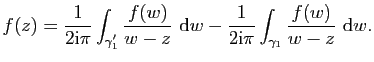
En reprenant la démonstration du Théorème d'analyticité des
fonctions holomorphes, on montre que la première intégrale a pour
valeur
![]() avec
avec
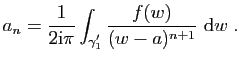
Pour la seconde intégrale, on remarque que si
![]() , on
a
, on
a
![]() . On peut donc écrire
. On peut donc écrire
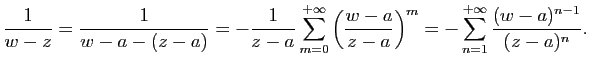
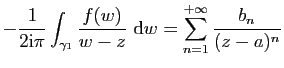
Pour calculer ![]() et
et ![]() on peut remplacer les chemins
on peut remplacer les chemins
![]() et
et ![]() par n'importe quel cercle
par n'importe quel cercle ![]() de
centre
de
centre ![]() et de rayon
et de rayon ![]() ,
, ![]() , orienté dans le sens direct
car si
, orienté dans le sens direct
car si ![]() n'est pas contenu dans la couronne
n'est pas contenu dans la couronne
![]()
Terminons en montrant l'unicité du développement de Laurent de ![]() .
Soient
.
Soient ![]() et
et ![]() deux nombres réels tels que
deux nombres réels tels que
![]() , supposons que
, supposons que
![]() pour tout
pour tout ![]() tel que
tel que
![]() . Puisque les
séries de Laurent convergent normalement sur tout compact de leur
couronne de définition, on peut échanger l'intégrale et la sommation
lors de l'intégration de la fonction
. Puisque les
séries de Laurent convergent normalement sur tout compact de leur
couronne de définition, on peut échanger l'intégrale et la sommation
lors de l'intégration de la fonction
![]() sur
le cercle
sur
le cercle ![]() de centre
de centre ![]() et de rayon r,
et de rayon r,
![]() . On
obtient alors pour tout
. On
obtient alors pour tout
![]()
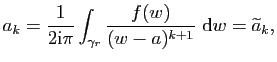
Singularités isolées et développement de Laurent
Soient
![]() ,
, ![]() et
et ![]() une fonction holomorphe dans le
disque épointé
une fonction holomorphe dans le
disque épointé
![]() . Elle possède
un développement de Laurent
. Elle possède
un développement de Laurent
![]() si
si
![]() . Alors
. Alors
(i) Si ![]() pour tout
pour tout ![]() ,
, ![]() est une singularité illusoire
pour
est une singularité illusoire
pour ![]() et
et ![]() se prolonge holomorpiquement au disque de centre
se prolonge holomorpiquement au disque de centre ![]() et de rayon
et de rayon ![]() par la série
par la série
![]() .
.
(ii) S'il existe ![]() tel que
tel que
![]() et
et ![]() si
si ![]() ,
,
![]() est un pôle d'ordre
est un pôle d'ordre ![]() de
de ![]() et la partie principale de
et la partie principale de ![]() en
en
![]() est
est
![]() .
.
(iii) S'il existe une infinité d'indices ![]() strictement négatifs
tels que
strictement négatifs
tels que ![]() , la fonction
, la fonction ![]() a une singularité essentielle
en
a une singularité essentielle
en ![]() . On dit encore que
. On dit encore que
![]() est la partie
principale de
est la partie
principale de ![]() en
en ![]() .
.
Ces trois cas représentant l'ensemble des possibilités et s'excluant mutuellement on a ainsi une caractérisation des singularités isolées d'une fonction holomorphe en fonction de son développement de Laurent.
De plus le coefficient ![]() du développement de Laurent de
du développement de Laurent de ![]() sur
sur ![]() s'appelle le résidu de
s'appelle le résidu de ![]() en
en ![]() .
.
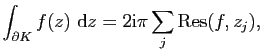
Soient
![]() les points singuliers de
les points singuliers de ![]() contenus dans
contenus dans
![]() . Pour
. Pour
![]() ,
,
![]() un disque fermé de centre
un disque fermé de centre ![]() et de rayon
et de rayon ![]() assez petit pour que
assez petit pour que
![]() soit contenu dans
soit contenu dans
![]() et
et
![]() si
si ![]() .
Soit
.
Soit ![]() le cercle orienté dans le sens direct bord de
le cercle orienté dans le sens direct bord de
![]() . Posons
. Posons
![]() ,
, ![]() est un
compact à bord dont le bord orienté est représenté par le cycle
est un
compact à bord dont le bord orienté est représenté par le cycle
![]() .
.
On peut appliquer le (ii) du Théorème 21 à la fonction
![]() et au cycle
et au cycle
![]() . On obtient
. On obtient
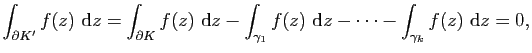
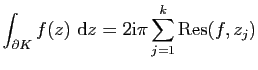
Le théorème de l'indice pour les fonctions méromorphes et le théorème de Rouché s'étendent également aux compacts à bord. On compte alors les zéros et les pôles contenu à l'intérieur du compact.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales