Soient
![]() et
et ![]() . On note
. On note
Si la fonction ![]() se prolonge en une fonction holomorphe sur
se prolonge en une fonction holomorphe sur ![]() (le prolongement est alors unique par le principe du prolongement
analytique), on dit que la singularité de
(le prolongement est alors unique par le principe du prolongement
analytique), on dit que la singularité de ![]() en
en ![]() est
illusoire ou éliminable ou encore que
est
illusoire ou éliminable ou encore que ![]() est une
fausse singularité ou un point régulier de
est une
fausse singularité ou un point régulier de ![]() .
.
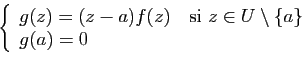
Puisque ![]() est holomorphe sur
est holomorphe sur
![]() et bornée au
voisinage de
et bornée au
voisinage de ![]() , la fonction
, la fonction ![]() est holomorphe sur
est holomorphe sur
![]() et continue sur
et continue sur ![]() donc holomorphe sur
donc holomorphe sur ![]() . Mais
si
. Mais
si ![]() est assez petit pour que
est assez petit pour que
![]() ,
, ![]() est
développable en série entière sur
est
développable en série entière sur ![]()
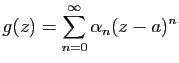 pour
pour
(i) La fonction ![]() a une singularité illusoire en
a une singularité illusoire en ![]() .
.
(ii) Il existe un entier
![]() , un réel
, un réel ![]() tel que
tel que
![]() et une fonction
et une fonction ![]() holomorphe sur le disque
holomorphe sur le disque
![]() vérifiant
vérifiant
![]() et
et
![]() pour
tout
pour
tout
![]() . On dit alors que
. On dit alors que ![]() a un pôle d'ordre
a un pôle d'ordre
![]() en
en ![]() .
.
(iii) Pour tout ![]() tel que
tel que
![]() , l'ensemble
, l'ensemble
![]() est dense dans
est dense dans
![]() . On dit alors que
. On dit alors que ![]() a une singularité essentielle en
a une singularité essentielle en ![]() .
.
Si
![]() ,
,
![]() a une fausse singularité en
a une fausse singularité en
![]() et (i) est vérifiée.
et (i) est vérifiée.
Si ![]() , notons
, notons ![]() la multiplicité du zéro
la multiplicité du zéro ![]() de
de ![]() . Il
existe alors une fonction
. Il
existe alors une fonction ![]() holomorphe sur
holomorphe sur ![]() vérifiant
vérifiant
![]() et telle que
et telle que
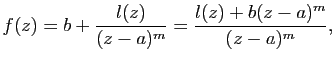
Fonctions méromorphes
Soient ![]() un ouvert connexe de
un ouvert connexe de
![]() et
et ![]() et
et ![]() deux fonctions
holomorphes sur
deux fonctions
holomorphes sur ![]() non identiquement nulles. D'après le principe
des zéros isolés, l'ensemble
non identiquement nulles. D'après le principe
des zéros isolés, l'ensemble ![]() des zéros de
des zéros de ![]() est une partie
localement finie de
est une partie
localement finie de ![]() . Considérons la fonction
. Considérons la fonction
![]() ,
elle est holomorphe sur
,
elle est holomorphe sur
![]() . Soient
. Soient ![]() et
et ![]() la
multiplicité du zéro
la
multiplicité du zéro ![]() de
de ![]() . Au voisinage de
. Au voisinage de ![]() on a
on a
Si
![]() , alors
, alors ![]() est un pôle de
est un pôle de ![]() . Si
. Si ![]() , on peut
écrire
, on peut
écrire
![]() avec
avec
![]() et
et ![]() holomorphe sur
holomorphe sur
![]() telle que
telle que
![]() puisque
puisque ![]() n'est pas identiquement
nulle. Ainsi
n'est pas identiquement
nulle. Ainsi
![]() , où
, où ![]() est une fonction
holomorphe au voisinage de
est une fonction
holomorphe au voisinage de ![]() . Si
. Si
![]() ,
, ![]() a une singularité
illusoire en
a une singularité
illusoire en ![]() et si
et si ![]() ,
, ![]() est un pôle d'ordre
est un pôle d'ordre ![]() de
de ![]() .
Dans tous les cas
.
Dans tous les cas ![]() est une fonction méromorphe sur
est une fonction méromorphe sur ![]() .
.
Remarque. En fait si ![]() est connexe, on peut prouver que toute fonction
est connexe, on peut prouver que toute fonction ![]() méromorphe sur
méromorphe sur ![]() s'écrit
s'écrit
![]() avec
avec ![]() et
et ![]() holomorphes dans
holomorphes dans ![]() et
et ![]() non identiquement nulle sur
non identiquement nulle sur ![]() .
.
Propriétés. Si ![]() est un ouvert de
est un ouvert de
![]() , la
réunion de deux parties localement finies de
, la
réunion de deux parties localement finies de ![]() est encore une
partie localement finie. On en déduit que la somme et le produit de
deux fonction méromorphes dans
est encore une
partie localement finie. On en déduit que la somme et le produit de
deux fonction méromorphes dans ![]() est encore une fonction
méromorphe dans
est encore une fonction
méromorphe dans ![]() et que
et que
![]() a une structure naturelle de
a une structure naturelle de
![]() -algèbre unitaire.
-algèbre unitaire.
(i) La dérivée ![]() de
de ![]() est méromorphe sur
est méromorphe sur ![]() et
et ![]() et
et ![]() ont
les mêmes pôles. Si
ont
les mêmes pôles. Si ![]() est un pôle d'ordre
est un pôle d'ordre ![]() de
de ![]() , c'est un
pôle d'ordre
, c'est un
pôle d'ordre ![]() de
de ![]() .
.
(ii) Supposons ![]() connexe et
connexe et ![]() non identiquement nulle sur
non identiquement nulle sur ![]() .
La fonction
.
La fonction
![]() est méromorphe sur
est méromorphe sur ![]() et les pôles de
et les pôles de
![]() sont simples.
sont simples.
Théorème des résidus
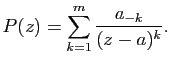
Démonstration : Puisque
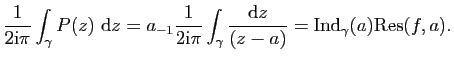
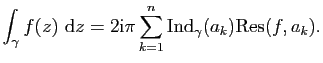
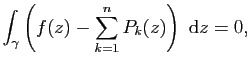
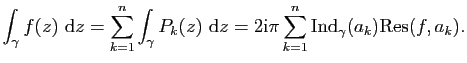
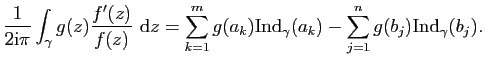
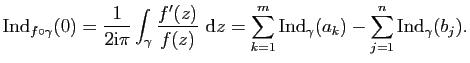
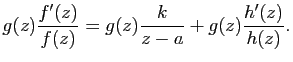
De même si ![]() est un pôle d'ordre
est un pôle d'ordre ![]() de
de ![]() , il existe alors
une fonction
, il existe alors
une fonction ![]() holomorphe au voisinage de
holomorphe au voisinage de ![]() telle que
telle que
![]() et
et
![]() et
et
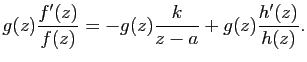
Le Théorème des résidus appliqué à la fonction ![]() donne alors le
résultat puisque les zéros et les pôles de
donne alors le
résultat puisque les zéros et les pôles de ![]() ont été comptés avec
leur ordre de multiplicité.
ont été comptés avec
leur ordre de multiplicité.![]() Remarque. On peut se passer de l'hypothèse de finitude sur l'ensemble des
zéros et des pôles de
Remarque. On peut se passer de l'hypothèse de finitude sur l'ensemble des
zéros et des pôles de ![]() , car on peut s'y ramener facilement. En
effet l'image
, car on peut s'y ramener facilement. En
effet l'image ![]() de
de ![]() est un compact de
est un compact de ![]() donc il
existe
donc il
existe
![]() et
et ![]() tels que
tels que
![]() .
Alors
.
Alors
![]() et
et ![]() étant un ouvert
relativement compact de
étant un ouvert
relativement compact de ![]() ,
, ![]() ne possède qu'un nombre fini
de zéros et de pôles dans
ne possède qu'un nombre fini
de zéros et de pôles dans ![]() . De plus si
. De plus si ![]() , on a
, on a
![]() car
car ![]() appartient alors à la composante connexe
non bornée de
appartient alors à la composante connexe
non bornée de
![]() car
car ![]() est étoilé.
est étoilé.
Le Théorème de l'indice permet d'obtenir de nouveaux résultats sur les suites de fonctions holomorphes.
(i) Si les fonctions ![]() ne s'annulent pas sur
ne s'annulent pas sur ![]() alors soit
alors soit ![]() est identiquement nulle sur
est identiquement nulle sur ![]() , soit
, soit ![]() ne s'annule pas sur
ne s'annule pas sur ![]() .
.
(ii) Si les fonctions ![]() sont injectives sur
sont injectives sur ![]() alors soit
alors soit ![]() est constante sur
est constante sur ![]() , soit
, soit ![]() est injective sur
est injective sur ![]() .
.
Montrons (i). Supposons que ![]() est n'est pas identiquement nulle et
que
est n'est pas identiquement nulle et
que ![]() est un zéro de
est un zéro de ![]() . D'après le principe des zéros
isolés il existe
. D'après le principe des zéros
isolés il existe ![]() tel que
tel que
![]() et
et
![]() , si
, si
![]() . Soit
. Soit ![]() le cercle de centre
le cercle de centre ![]() et de
rayon
et de
rayon ![]() parcouru dans le sens direct. D'après le Théorème de
l'indice, il existe
parcouru dans le sens direct. D'après le Théorème de
l'indice, il existe
![]() tel que
tel que
![]() et
et
![]() pour tout
pour tout
![]() car les
car les ![]() ne
s'annulent pas dans
ne
s'annulent pas dans ![]() .
.
Comme
![]() si
si ![]() , il existe
, il existe ![]() tel que
tel que
![]() si
si ![]() , soit encore
, soit encore
![]() si
si
![]() . De plus d'après le Théorème de Weierstraß, la suite
. De plus d'après le Théorème de Weierstraß, la suite
![]() converge uniformément sur tout compact de
converge uniformément sur tout compact de ![]() , en
particulier sur le cercle de centre
, en
particulier sur le cercle de centre ![]() et de rayon
et de rayon ![]() , image de
, image de
![]() , donc la suite
, donc la suite
![]() converge
uniformément vers
converge
uniformément vers
![]() sur le cercle de centre
sur le cercle de centre ![]() et de rayon
et de rayon ![]() .
.
Par conséquent
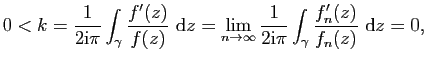
Prouvons (ii) maintenant. Supposons que ![]() n'est pas constante et
qu'il existe des points
n'est pas constante et
qu'il existe des points ![]() et
et ![]() de
de ![]() tels que
tels que ![]() .
Soient
.
Soient ![]() et
et ![]() des disque ouverts de centre respectif
des disque ouverts de centre respectif ![]() et
et
![]() , contenus dans
, contenus dans ![]() et disjoints. Puisque
et disjoints. Puisque ![]() n'est pas
identiquement nulle sur
n'est pas
identiquement nulle sur ![]() , car
, car ![]() n'est pas constante, il
résulte de (i) qu'il existe une suite extraite
n'est pas constante, il
résulte de (i) qu'il existe une suite extraite
![]() de la suite
de la suite
![]() telle que
telle que
![]() ait un zéro dans
ait un zéro dans ![]() pour tout
pour tout
![]() . De
même une nouvelle extraction donne l'existence d'une suite extraite
. De
même une nouvelle extraction donne l'existence d'une suite extraite
![]() de la suite
de la suite
![]() telle que
telle que
![]() ait un zéro dans
ait un zéro dans ![]() pour tout
pour tout
![]() . Comme
. Comme
![]() et
et ![]() sont disjoints, les fonctions
sont disjoints, les fonctions
![]() ne sont
donc pas injectives puisque
ne sont
donc pas injectives puisque ![]() , ce qui contredit
l'hypothèse.
, ce qui contredit
l'hypothèse.![]()
(i) la fonction ![]() (resp.
(resp. ![]() ) n'a qu'un nombre fini
) n'a qu'un nombre fini
![]() (resp.
(resp.
![]() ) de zéros dans
) de zéros dans ![]() comptés
avec leur ordre de multiplicité,
comptés
avec leur ordre de multiplicité,
(ii) pour tout
![]() , on a
, on a
![]() ,
,
alors
![]() .
.
Prouvons tout d'abord le lemme suivant :
Posons
![]() , alors
, alors
![]() .
L'hypothèse implique
.
L'hypothèse implique
![]() pour tout
pour tout
![]() et donc l'image de
et donc l'image de ![]() est contenue dans le
disque de centre
est contenue dans le
disque de centre ![]() et de rayon
et de rayon ![]() . Par conséquent 0 appartient
à la composante connexe non bornée de
. Par conséquent 0 appartient
à la composante connexe non bornée de
![]() et donc
et donc
![]() , d'où
, d'où
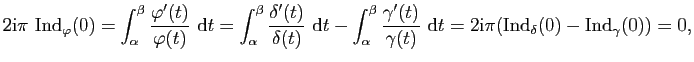
Démonstration : [du Théorème de Rouché]
L'hypothèse implique que si
![]() ,
,
![]() et
et
![]() et que si
et que si
![]() on a
on a
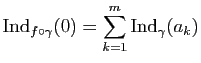
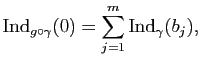
Nous en déduisons facilement le corollaire suivant :
Comme application de ce corollaire nous pouvons donner une nouvelle démonstration du Théorème de d'Alembert.
Soit
![]() , un polynôme de degré
, un polynôme de degré ![]() . On
pose
. On
pose
![]() et
et
![]() . Puisque
. Puisque ![]() est polynôme de
degré
est polynôme de
degré ![]() , il existe
, il existe ![]() tel que pour
tel que pour ![]() on ait
on ait
![]() . Par conséquent
. Par conséquent ![]() et
et ![]() ne s'annulent pas
pour
ne s'annulent pas
pour
![]() et d'après le corollaire 10
et d'après le corollaire 10 ![]() et
et ![]() ont le même nombre de zéros dans le disque de centre 0 et de rayon
ont le même nombre de zéros dans le disque de centre 0 et de rayon
![]() , soit
, soit ![]() . Le polynôme
. Le polynôme ![]() possède donc exactement
possède donc exactement ![]() racines
dans
racines
dans
![]() .
.
Étude locale des applications holomorphes
Dans cette partie nous allons préciser grâce au Théorème de l'indice les propriétés locales des fonctions holomorphes que nous avons déjà démontrées comme le Théorème de l'application ouverte et le Théorème d'inversion locale.
Comme les zéros de ![]() et de
et de ![]() sont isolés, il existe
sont isolés, il existe
![]() tel que le disque fermé
tel que le disque fermé
![]() de centre
de centre ![]() et de
rayon
et de
rayon ![]() soit contenu dans le domaine de définition de
soit contenu dans le domaine de définition de ![]() et tel
que
et tel
que
![]() et
et
![]() pour tout
pour tout
![]() . Soit
. Soit ![]() le cercle de
centre
le cercle de
centre ![]() et de rayon
et de rayon ![]() orienté dans le sens direct. D'après le
Théorème de l'indice on a
orienté dans le sens direct. D'après le
Théorème de l'indice on a
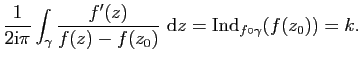
Puisque l'indice
![]() est constant
sur la composante connexe
est constant
sur la composante connexe ![]() de
de
![]() qui contient
qui contient ![]() , on a
, on a
![]() pour tout
pour tout ![]() . D'après le Théorème de
l'indice, l'équation
. D'après le Théorème de
l'indice, l'équation
Remarque.
Terminons en donnant une démonstration directe (sans passer par le calcul différentiel) du Théorème d'inversion locale pour les fonctions holomorphes.
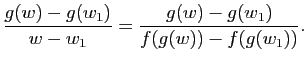
Grâce au Théorème de l'indice, sous les hypothèses du Théorème
19, on peut expliciter l'application ![]() inverse locale de
inverse locale de
![]() à l'aide d'une formule intégrale.
à l'aide d'une formule intégrale.
Formule d'inversion locale. Considérons ![]() et
et
![]() les voisinages de
les voisinages de ![]() et de
et de
![]() du Théorème 19
et supposons que
du Théorème 19
et supposons que ![]() (i.e.
(i.e.
![]() ). D'après le Théorème
de l'indice, la solution
). D'après le Théorème
de l'indice, la solution ![]() de l'équation
de l'équation ![]() , pour
, pour ![]() est donnée par
est donnée par
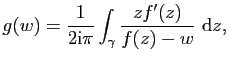
Plus généralement, pour toute fonction ![]() holomorphe sur
holomorphe sur ![]() , on a
, on a
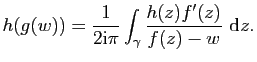
La formule intégrale donnant ![]() permet également de prouver
directement que
permet également de prouver
directement que
![]() est holomorphe sur
est holomorphe sur ![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales