Propriétés élémentaires des fonctions
holomorphes
Nous décrivons ici les propriétés des fonctions holomorphes qui sont
des conséquences directes de la formule de Cauchy pour les disques.
Inégalités de Cauchy
Le théorème suivant montre que, si  est une fonction holomorphe,
toutes les dérivées de
est une fonction holomorphe,
toutes les dérivées de  en un point sont contrôlées par les
valeurs de
en un point sont contrôlées par les
valeurs de  au voisinage de ce point.
au voisinage de ce point.
Démonstration : D'après le Corollaire 1, la fonction  étant holomorphe
dans le disque
étant holomorphe
dans le disque 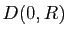 , elle est développable en série entière dans
ce disque et on a pour tout
, elle est développable en série entière dans
ce disque et on a pour tout 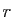 tel que
tel que 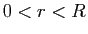 ,
,
Si on pose
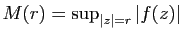 , on a alors pour
, on a alors pour
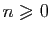

Démonstration : Puisque  est holomorphe dans
est holomorphe dans
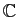 , il résulte du Corollaire
1 que
, il résulte du Corollaire
1 que  est développable en série entière, soit
est développable en série entière, soit
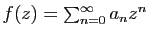 pour tout
pour tout
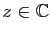 . De plus il
existe
. De plus il
existe 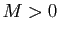 tel que
tel que
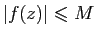 pour tout
pour tout
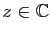 , puisque
, puisque  est bornée. Les inégalités de Cauchy donnent alors
est bornée. Les inégalités de Cauchy donnent alors
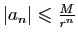 pour tout
pour tout 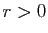 et tout
et tout
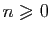 , ce qui implique
, ce qui implique
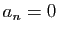 , si
, si
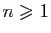 .
.
Corollaire 4 (Théorème de d'Alembert)
Tout polynôme à coefficients complexes
non constant possède au moins une racine.
Démonstration : Raisonnons par l'absurde. Soit
![$ P\in\mathbb{C}[X]$](img275.gif) un polynôme de degré
strictement supérieur à
un polynôme de degré
strictement supérieur à 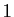 , supposons que
, supposons que 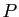 n'admet pas de racine
dans
n'admet pas de racine
dans
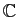 . La fonction
. La fonction
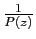 est alors entière et bornée
puisque
est alors entière et bornée
puisque
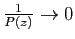 quand
quand
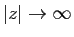 , elle est donc
constante par le Théorème de Liouville, d'où la contradiction.
, elle est donc
constante par le Théorème de Liouville, d'où la contradiction.
Suites et séries de fonctions
holomorphes
Nous allons voir comment les inégalités de Cauchy simplifient
l'étude des suites et séries de fonctions dans le cas des fonctions
holomorphes d'une variable complexe par rapport au cas des fonctions
de classe
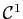 d'une ou plusieurs variables réelles.
d'une ou plusieurs variables réelles.
Rappels
1) Si une suite
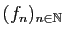 de fonctions continues sur
de fonctions continues sur  converge uniformément sur tout compact de
converge uniformément sur tout compact de  vers une fonction
vers une fonction  ,
alors la fonction
,
alors la fonction  est continue sur
est continue sur  .
.
2) Soient  un ouvert convexe de
un ouvert convexe de
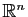 ,
,
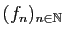 une
suite d'applications de classe
une
suite d'applications de classe
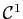 de
de  dans
dans
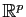 et
et 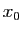 un point de
un point de  . Si la suite
. Si la suite
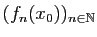 converge et si
la suite
converge et si
la suite
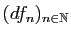 converge uniformément sur tout compact
de
converge uniformément sur tout compact
de  vers
vers
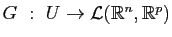 , alors la suite
, alors la suite
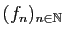 converge uniformément sur tout compact de
converge uniformément sur tout compact de  vers
une application
vers
une application  de classe
de classe
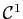 telle que
telle que 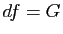 .
.
Démonstration : Montrons tout d'abord la seconde assertion du théorème. Soit 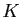 un
compact de
un
compact de  et
et
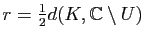 si
si
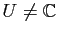 et
et  si
si
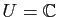 , alors pour tout
, alors pour tout 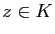 le disque fermé
le disque fermé
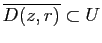 .
.
Soit
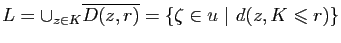 ,
,
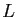 est une partie compacte de
est une partie compacte de  . Les inégalités de Cauchy
appliquées à la fonction
. Les inégalités de Cauchy
appliquées à la fonction 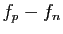 impliquent que pour tout
impliquent que pour tout 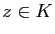
Puisque la suite
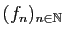 converge uniformément sur
converge uniformément sur 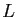 , on en déduit que les suites
, on en déduit que les suites
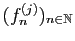 sont uniformément de Cauchy sur
sont uniformément de Cauchy sur 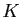 et par
conséquent convergent uniformément sur
et par
conséquent convergent uniformément sur 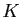 . Il suffit alors
d'appliquer à la suite
. Il suffit alors
d'appliquer à la suite
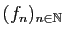 l'assertion 2) du rappel au
voisinage de chaque point de
l'assertion 2) du rappel au
voisinage de chaque point de  , car
, car
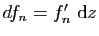 .
.
Démonstration : L'assertion (i) résulte du Théorème 4 en considérant
la suite des sommes partielles de la série
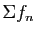 .
.
Montrons l'assertion (ii). Soit 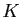 un compact de
un compact de  et
et 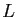 défini
comme dans la preuve du Théorème 4. Les inégalités de
Cauchy donnent alors
défini
comme dans la preuve du Théorème 4. Les inégalités de
Cauchy donnent alors
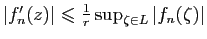 pour tout
pour tout 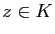 , soit
, soit
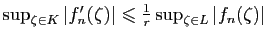 , ce
qui prouve (ii).
, ce
qui prouve (ii).
Intégrales dépendant d'un paramètre
Soient 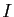 un intervalle de
un intervalle de
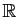 ,
, 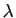 la mesure de Lebesgue
sur
la mesure de Lebesgue
sur 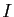 et
et  un ouvert de
un ouvert de
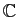 . On considère une fonction
. On considère une fonction  définie sur
définie sur 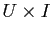 et à valeurs dans
et à valeurs dans
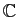 .
.
On suppose que, pour tout 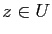 , l'application
, l'application
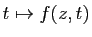 est
est 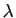 -intégrable. Soit alors
-intégrable. Soit alors 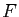 la fonction définie sur
la fonction définie sur  par
par
Remarque. L'existence de la fonction majorante 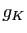 est trivialement vérifiée
si
est trivialement vérifiée
si  est continue sur
est continue sur 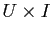 et si
et si 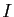 est compact (il suffit
alors de prendre pour
est compact (il suffit
alors de prendre pour 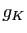 une fonction constante, la fonction
une fonction constante, la fonction  étant bornée sur le compact
étant bornée sur le compact 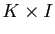 ).
Démonstration : Montrons tout d'abord que
).
Démonstration : Montrons tout d'abord que
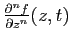 vérifie des
majorations analogues à celles vérifiées par
vérifie des
majorations analogues à celles vérifiées par 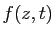 . Le compact
. Le compact
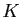 de
de  étant fixé, on considère le compact
étant fixé, on considère le compact 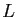 de
de  défini par
défini par
où
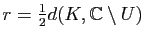 si
si
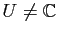 et
et  si
si
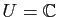 .
.
Les inégalités de Cauchy donnent
soit encore
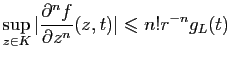 |
(4) |
pour tout 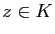 et tout
et tout 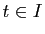 .
.
Par ailleurs on a pour tout 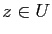
la fonction
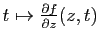 est donc
est donc 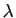 -mesurable comme limite simple
d'une suite de fonctions
-mesurable comme limite simple
d'une suite de fonctions 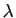 -mesurables. Par récurrence sur
-mesurables. Par récurrence sur
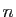 , on montre que
, on montre que
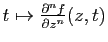 est
également
est
également 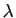 -mesurable. La majoration (4) prouve
alors que
-mesurable. La majoration (4) prouve
alors que
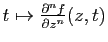 est
est
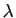 -intégrable, on peut donc considérer la fonction sur
-intégrable, on peut donc considérer la fonction sur  définie par
définie par
Montrons maintenant que 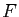 est holomorphe sur
est holomorphe sur  . Soit
. Soit 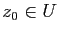 fixé et
fixé et 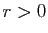 tel que le disque fermé
tel que le disque fermé
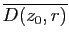 soit contenu
dans
soit contenu
dans  . Posons
. Posons
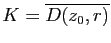 . Pour
. Pour
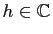 tel que
tel que
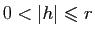 on a
on a
Si 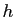 tend vers 0 en
restant non nul, la fonction
tend vers 0 en
restant non nul, la fonction
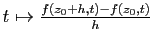 tend vers la fonction
tend vers la fonction
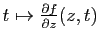 . D'autre part
. D'autre part
d'où
qui est une fonction 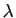 -intégrable indépendante de
-intégrable indépendante de 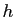 ,
d'après(4). On déduit alors du théorème convergence
dominée de Lebesgue que
,
d'après(4). On déduit alors du théorème convergence
dominée de Lebesgue que
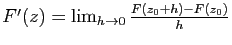 existe et que
existe et que
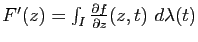 . Une récurrence élémentaire termine la
démonstration du théorème.
. Une récurrence élémentaire termine la
démonstration du théorème.
Exemple :
On considère la fonction 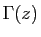 définie par l'intégrale
définie par l'intégrale
pour
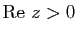 .
.
Soient
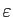 et
et 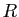 deux réels strictement positifs, sur
l'ensemble des
deux réels strictement positifs, sur
l'ensemble des
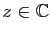 tels que
tels que
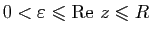 , la fonction
, la fonction
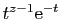 possède une fonction majorante
intégrable indépendante de
possède une fonction majorante
intégrable indépendante de 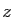 car
car
La fonction 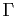 est donc holomorphe dans le demi-plan
est donc holomorphe dans le demi-plan
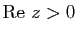 et dans ce demi-plan on a
et dans ce demi-plan on a
Propriété de la moyenne et
principe du maximum
Remarque. Si  possède la propriété de la moyenne, il en est de même de
possède la propriété de la moyenne, il en est de même de
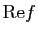 et
et
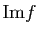 .
.
Proposition 5
Si  est holomorphe dans
est holomorphe dans  ,
,  a la propriété de la moyenne
dans
a la propriété de la moyenne
dans  .
.
Démonstration : Si 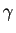 désigne le cercle de centre
désigne le cercle de centre 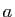 et de rayon
et de rayon 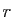 oriénté
dans le sens positif, la formule de Cauchy donne
oriénté
dans le sens positif, la formule de Cauchy donne

Théorème 7
Une fonction  définie et continue sur un ouvert
définie et continue sur un ouvert  de
de
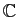 , qui
possède la propriété de la moyenne, vérifie le principe du maximum.
, qui
possède la propriété de la moyenne, vérifie le principe du maximum.
Démonstration : Soit 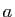 un maximum relatif de
un maximum relatif de  et
et 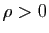 tel que
tel que
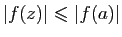 pour tout
pour tout
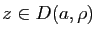 .
.
Si 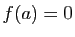 , le théorème est évident, en effet
, le théorème est évident, en effet 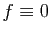 dans
dans
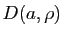 .
.
Si
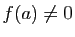 , quitte à multiplier
, quitte à multiplier  par une constante
convenable (
par une constante
convenable (
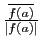 par exemple) on peut supposer
que
par exemple) on peut supposer
que
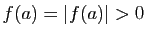 . Pour tout
. Pour tout 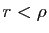 , la propriété de la moyenne
s'écrit
, la propriété de la moyenne
s'écrit
d'où
En particulier en prenant la partie réelle
![$\displaystyle \frac{1}{2\pi}\int_0^{2\pi}[\vert f(a)\vert-\mathrm{Re} f(a+r\mathrm{e}^{\mathrm{i}t})] \mathrm{d}t=0.$](img375.gif) |
(5) |
Mais puisque 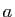 est un maximum relatif de
est un maximum relatif de  , la fonction continue
, la fonction continue
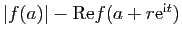 est positive ou nulle. La nullité de
(5) implique pour tout
est positive ou nulle. La nullité de
(5) implique pour tout 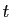 et tout
et tout 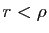 que
que
Or
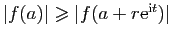 donc
donc
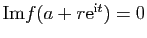 et
et
pour tout 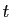 et tout
et tout 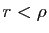 .
.
Corollaire 5
Si  est un ouvert connexe et
est un ouvert connexe et  une fonction holomorphe non
constante sur
une fonction holomorphe non
constante sur  ,
,  n'admet pas de maximum relatif dans
n'admet pas de maximum relatif dans  .
.
Démonstration : Raisonnons par l'absurde, supposons que  possède un maximum
relatif en
possède un maximum
relatif en 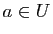 . Puisque
. Puisque  est holomorphe, elle satisfait la
propriété de la moyenne et d'après le Théorème 7 elle est
donc constante au voisinage de
est holomorphe, elle satisfait la
propriété de la moyenne et d'après le Théorème 7 elle est
donc constante au voisinage de 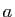 . L'analyticité de
. L'analyticité de  et la
connexité de
et la
connexité de  impliquent alors que
impliquent alors que  est constante, ce qui
contredit l'hypothèse.
est constante, ce qui
contredit l'hypothèse.
Corollaire 6
Si  est un ouvert connexe et
est un ouvert connexe et  une fonction holomorphe non
constante sur
une fonction holomorphe non
constante sur  telle que
telle que 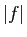 admet un minimum local dans
admet un minimum local dans  ,
alors ce minimum est nécessairement nul. En particulier
,
alors ce minimum est nécessairement nul. En particulier  s'annule
au moins une fois dans
s'annule
au moins une fois dans  .
.
Démonstration : Soit 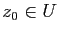 un minimum local pour
un minimum local pour 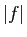 . Supposons que
. Supposons que
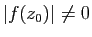 , alors
, alors
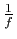 est définie et holomorphe au
voisinage de
est définie et holomorphe au
voisinage de 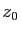 et possède un maximum local en
et possède un maximum local en 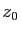 , donc
, donc  est constante d'après le principe du maximum (Corollaire
5, ce qui contredit l'hypothèse.
est constante d'après le principe du maximum (Corollaire
5, ce qui contredit l'hypothèse.
Nous donnons maintenant une formulation plus globale du principe du
maximum.
Proposition 6
Soit  un domaine (i.e. ouvert connexe) borné de
un domaine (i.e. ouvert connexe) borné de
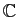 et
et  une
fonction continue sur
une
fonction continue sur
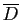 et holomorphe sur
et holomorphe sur  . Soit
. Soit
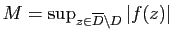 , alors
, alors
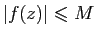 pour
tout
pour
tout 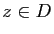 . De plus, s'il existe
. De plus, s'il existe 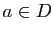 tel que
tel que 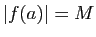 ,
alors
,
alors  est constante sur
est constante sur  .
.
Démonstration : Soit
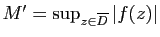 , comme
, comme  est continue sur
est continue sur
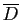 , qui est compact, cette borne supérieure est atteinte en au moins
un point de
, qui est compact, cette borne supérieure est atteinte en au moins
un point de
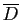 . Si elle est atteint en un point
. Si elle est atteint en un point 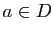 , alors
, alors
 est constante au voisinage de
est constante au voisinage de 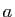 et donc constante sur l'ouvert
connexe
et donc constante sur l'ouvert
connexe  par prolongement analytique. Sinon
par prolongement analytique. Sinon 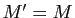 car la borne
supérieure est alors atteinte sur
car la borne
supérieure est alors atteinte sur
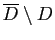 et pour tout
et pour tout
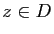 on a
on a
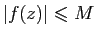 .
.
Démonstration : Dans 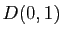 la fonction
la fonction  coïncide avec sa série de Taylor en
0, i.e.
coïncide avec sa série de Taylor en
0, i.e.
Or par hypothèse 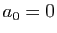 car
car 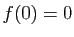 et par conséquent la fonction
et par conséquent la fonction
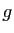 définie par
définie par
est holomorphe sur le disque 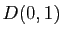 .
.
Puisque 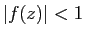 , on a
, on a
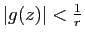 si
si 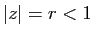 . Cette
inégalité est encore valable pour
. Cette
inégalité est encore valable pour
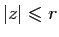 , d'après la variante
du principe du maximum, par conséquent en faisant tendre
, d'après la variante
du principe du maximum, par conséquent en faisant tendre 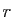 vers
vers
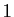 on a
on a 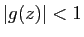 , soit
, soit
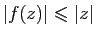 pour tout
pour tout
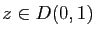 .
.
De plus s'il existe
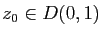 tel que
tel que 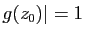 alors ,
d'après la Proposition 6, la fonction
alors ,
d'après la Proposition 6, la fonction 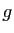 est constante
égale à
est constante
égale à 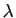 , où
, où
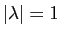 et
et
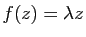 pour tout
pour tout
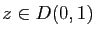 .
.
Terminons cette section en prouvant le théorème de l'application
ouverte pour les fonctions holomorphes à l'aide du principe du
maximum.
Démonstration : Soient 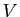 un ouvert de
un ouvert de  et
et 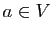 , nous devons prouver que
, nous devons prouver que
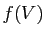 est un voisinage de
est un voisinage de 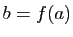 .
.
Comme  n'est pas constante, on peut trouver d'après le principe
des zéros isolés un disque ouvert
n'est pas constante, on peut trouver d'après le principe
des zéros isolés un disque ouvert  centré en
centré en 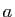 tel que
tel que
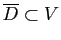 et
et 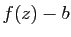 ne s'annule pas sur
ne s'annule pas sur
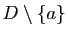 . Soit
. Soit
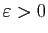 tel que
tel que
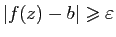 sur
sur
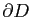 ( un
tel
( un
tel
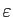 existe par compacité de
existe par compacité de
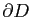 . On va montrer que
. On va montrer que
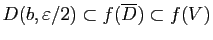 .
.
Fixons
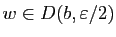 et considérons la fonction
et considérons la fonction 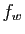 de
de
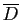 dans
dans
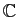 définie par
définie par
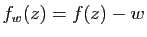 . La fonction
. La fonction 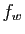 est continue donc la fonction
est continue donc la fonction 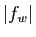 atteint sa borne inférieure
sur le compact
atteint sa borne inférieure
sur le compact
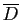 . Par ailleurs
. Par ailleurs
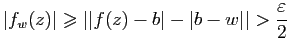
si

et
On en déduit que la borne inférieure de 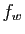 est atteinte en point
de
est atteinte en point
de  . Comme
. Comme  n'est pas constante dans dans
n'est pas constante dans dans  , puisque
, puisque  ne l'est pas, la fonction
ne l'est pas, la fonction
 s'annule au moins une fois
dans
s'annule au moins une fois
dans  d'après le Corollaire 6, ce qui signifie que
d'après le Corollaire 6, ce qui signifie que  .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est une fonction holomorphe,
toutes les dérivées de
est une fonction holomorphe,
toutes les dérivées de ![]() en un point sont contrôlées par les
valeurs de
en un point sont contrôlées par les
valeurs de ![]() au voisinage de ce point.
au voisinage de ce point.
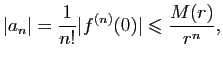
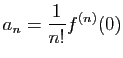
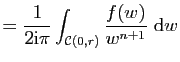
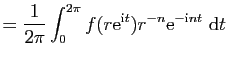
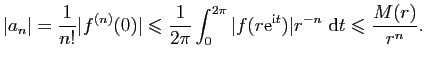
![]() d'une ou plusieurs variables réelles.
d'une ou plusieurs variables réelles.
![]() de fonctions continues sur
de fonctions continues sur ![]() converge uniformément sur tout compact de
converge uniformément sur tout compact de ![]() vers une fonction
vers une fonction ![]() ,
alors la fonction
,
alors la fonction ![]() est continue sur
est continue sur ![]() .
.
![]() un ouvert convexe de
un ouvert convexe de
![]() ,
,
![]() une
suite d'applications de classe
une
suite d'applications de classe
![]() de
de ![]() dans
dans
![]() et
et ![]() un point de
un point de ![]() . Si la suite
. Si la suite
![]() converge et si
la suite
converge et si
la suite
![]() converge uniformément sur tout compact
de
converge uniformément sur tout compact
de ![]() vers
vers
![]() , alors la suite
, alors la suite
![]() converge uniformément sur tout compact de
converge uniformément sur tout compact de ![]() vers
une application
vers
une application ![]() de classe
de classe
![]() telle que
telle que ![]() .
.
![]() ,
,
![]() est une partie compacte de
est une partie compacte de ![]() . Les inégalités de Cauchy
appliquées à la fonction
. Les inégalités de Cauchy
appliquées à la fonction ![]() impliquent que pour tout
impliquent que pour tout ![]()
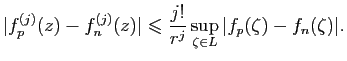
![]() est holomorphe sur
est holomorphe sur ![]() et la série
et la série
![]() converge uniformément sur tout compact de
converge uniformément sur tout compact de ![]() vers
vers ![]() ;
;
![]() est normalement convergente sur tout
compact de
est normalement convergente sur tout
compact de ![]() , il en est de même de la série
, il en est de même de la série
![]() .
.![]() un compact de
un compact de ![]() et
et ![]() défini
comme dans la preuve du Théorème 4. Les inégalités de
Cauchy donnent alors
défini
comme dans la preuve du Théorème 4. Les inégalités de
Cauchy donnent alors
![]() pour tout
pour tout ![]() , soit
, soit
![]() , ce
qui prouve (ii).
, ce
qui prouve (ii).![]()
![]() un intervalle de
un intervalle de
![]() ,
, ![]() la mesure de Lebesgue
sur
la mesure de Lebesgue
sur ![]() et
et ![]() un ouvert de
un ouvert de
![]() . On considère une fonction
. On considère une fonction ![]() définie sur
définie sur ![]() et à valeurs dans
et à valeurs dans
![]() .
.
![]() , l'application
, l'application
![]() est
est ![]() -intégrable. Soit alors
-intégrable. Soit alors ![]() la fonction définie sur
la fonction définie sur ![]() par
par
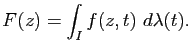
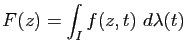
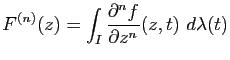
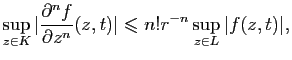
![]()
![$\displaystyle \frac{\partial f}{\partial z}(z,t)=\lim_{k\to\infty}
k[f(z+\frac{1}{k},t)-f(z,t)],$](img328.gif)
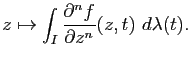
![]() est holomorphe sur
est holomorphe sur ![]() . Soit
. Soit ![]() fixé et
fixé et ![]() tel que le disque fermé
tel que le disque fermé
![]() soit contenu
dans
soit contenu
dans ![]() . Posons
. Posons
![]() . Pour
. Pour
![]() tel que
tel que
![]() on a
on a
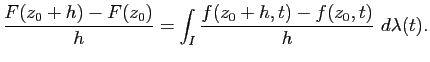
![$\displaystyle f(z_0+h,t)-f(z_0,t)=\int_{[z_0,z_0+h]} \frac{\partial f}{\partial z}
(\zeta,t) d\zeta,$](img340.gif)

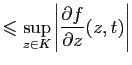
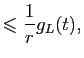
![]() définie par l'intégrale
définie par l'intégrale
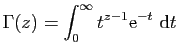
![]() et
et ![]() deux réels strictement positifs, sur
l'ensemble des
deux réels strictement positifs, sur
l'ensemble des
![]() tels que
tels que
![]() , la fonction
, la fonction
![]() possède une fonction majorante
intégrable indépendante de
possède une fonction majorante
intégrable indépendante de ![]() car
car
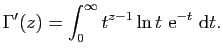
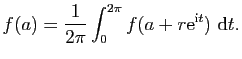
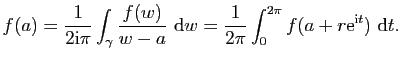
![]() vérifie le principe du maximum dans
vérifie le principe du maximum dans ![]() si
pour tout maximum relatif
si
pour tout maximum relatif ![]() de
de ![]() ,
, ![]() est constante au
voisinage de
est constante au
voisinage de ![]() .
.![]() , le théorème est évident, en effet
, le théorème est évident, en effet ![]() dans
dans
![]() .
.
![]() , quitte à multiplier
, quitte à multiplier ![]() par une constante
convenable (
par une constante
convenable (
![]() par exemple) on peut supposer
que
par exemple) on peut supposer
que
![]() . Pour tout
. Pour tout ![]() , la propriété de la moyenne
s'écrit
, la propriété de la moyenne
s'écrit
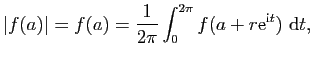
![$\displaystyle \frac{1}{2\pi}\int_0^{2\pi}[\vert f(a)\vert-f(a+r\mathrm{e}^{\mathrm{i}t})] \mathrm{d}t=0.$](img374.gif)
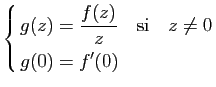
![]() , on a
, on a
![]() si
si ![]() . Cette
inégalité est encore valable pour
. Cette
inégalité est encore valable pour
![]() , d'après la variante
du principe du maximum, par conséquent en faisant tendre
, d'après la variante
du principe du maximum, par conséquent en faisant tendre ![]() vers
vers
![]() on a
on a ![]() , soit
, soit
![]() pour tout
pour tout
![]() .
.
![]() tel que
tel que ![]() alors ,
d'après la Proposition 6, la fonction
alors ,
d'après la Proposition 6, la fonction ![]() est constante
égale à
est constante
égale à ![]() , où
, où
![]() et
et
![]() pour tout
pour tout
![]() .
.![]()
![]() n'est pas constante, on peut trouver d'après le principe
des zéros isolés un disque ouvert
n'est pas constante, on peut trouver d'après le principe
des zéros isolés un disque ouvert ![]() centré en
centré en ![]() tel que
tel que
![]() et
et ![]() ne s'annule pas sur
ne s'annule pas sur
![]() . Soit
. Soit
![]() tel que
tel que
![]() sur
sur
![]() ( un
tel
( un
tel
![]() existe par compacité de
existe par compacité de
![]() . On va montrer que
. On va montrer que
![]() .
.
![]() et considérons la fonction
et considérons la fonction ![]() de
de
![]() dans
dans
![]() définie par
définie par
![]() . La fonction
. La fonction ![]() est continue donc la fonction
est continue donc la fonction ![]() atteint sa borne inférieure
sur le compact
atteint sa borne inférieure
sur le compact
![]() . Par ailleurs
. Par ailleurs
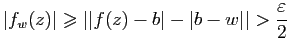 si
si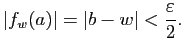
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales