Section : Cours
Avant : Théorie de Cauchy globale
Après : Entraînement

Topologie de $ \mathcal {H}(U)$ et représentation conforme

Rappels sur les espaces vectoriels topologiques

L'objet de cette section est de rappeler les propriétés basiques des espaces vectoriels topologiques, tout particulièrement lorsque la topologie est définie par une famille de semi-normes.

Soit $ E$ un espace vectoriel sur $ K=\mathbb{R}$ ou $ \mathbb{C}$, on dira qu'une partie $ A$ de $ E$ est absorbante si pour tout $ x\in E$ il existe $ \alpha>0$ tel que $ \lambda x\in A$ lorsque $ \lambda\in K$ et $ \vert\lambda\vert<\alpha$ et on dira qu'elle est équilibrée si $ \lambda A\subset A$ pour tout $ \lambda\in K$ tel que $ \vert\lambda\vert<1$. Remarquons que si une partie $ A$ de $ E$ est absorbante alors $ 0\in A$.

Définition 16   Un espace topologique $ E$ muni d'une structure algébrique d'espace vectoriel sur $ K=\mathbb{R}$ ou $ \mathbb{C}$ est un espace vectoriel topologique, en abbrégé evt, si les lois définissant la structure d'espace vectoriel sont continues, plus précisément si la loi de composition interne $ + : E\times E\to E$ est continue et si la loi externe $ K\times E\to E$ est elle aussi continue lorsqu'on munit $ K$ de sa topologie usuelle.

Puisque par définition dans un evt les translations sont des homéomorphismes, une topologie d'evt sur un espace vectoriel $ E$ est caractérisée par la donnée d'un système fondamental $ \widetilde{\mathcal{V}}(0)$ de voisinages de 0 et pour chaque point $ x\in E$ un système fondamental de voisinage $ \widetilde{\mathcal{V}}(x)$ est alors donné par $ \widetilde{\mathcal{V}}(x)=\{x+V \vert V\in\widetilde{\mathcal{V}}(0)\}$.

Les propriétés de continuité des deux lois définissant la structure algébrique d'espace vectoriel impliquent que l'ensemble $ \mathcal{V}(0)$ des voisinages de 0 d'une topologie d'evt satisfait l'ensemble de propiétes $ (V0)$ suivant :

(i) Si $ V\in\mathcal{V}(0)$ et si $ W\supset V$ alors $ W\in\mathcal{V}(0)$;

(ii) Si $ V_1,\dots,V_n\in\mathcal{V}(0)$ alors $ V_1\cap\dots\cap V_n\in\mathcal{V}(0)$;

(iii) Si $ V\in\mathcal{V}(0)$, il existe $ W\in\mathcal{V}(0)$ tel que $ W+W\subset V$;

(iv) Si $ V\in\mathcal{V}(0)$ et si $ \lambda\in K\setminus\{0\}$ alors $ \lambda V\in\mathcal{V}(0)$;

(v) Si $ V\in\mathcal{V}(0)$, $ V$ est absorbant;

(vi) $ \mathcal{V}(0)$ possède un système fondamental de voisinages équilibrés.

En fait cet ensemble de propriétés caractérise une topologie d'evt sur un espace vectoriel comme l'indique la proposition suivante :

Proposition 10   Soit E un espace vectoriel et $ \mathcal{V}(0)$ un ensemble de parties de $ E$ vérifiant les propriétés (V0), il existe alors une unique topologie sur $ E$ qui fait de $ E$ un espace vectoriel topologique, admettant pour tout $ x\in A$, $ x+\mathcal{V}(0)$ comme ensemble de voisinages de $ x$.

Définition 17   Une application $ p$ d'un espace vectoriel $ E$ sur $ K=\mathbb{R}$ ou $ \mathbb{C}$ à valeur dans $ \mathbb{R}$ est unesemi-norme si et seulement si

(1) $ p(x)\geqslant 0$ pour tout $ x\in E$ et $ p(0)=0$;

(2) $ p(\lambda x)=\vert\lambda\vert p(x)$ pour tout $ x\in E$ et tout $ \lambda\in K$;

(3) $ p(x+y)\leqslant p(x)+p(y)$ pour tout $ (x,y)\in E\times E$.

On obtient une topologie d'evt sur un espace vectoriel muni d'une famille de semi-normes $ (p_i)_{i\in I}$ en définissant un système fondamental de voisinages 0 en posant

$\displaystyle \widetilde{\mathcal{V}}(0)=\left\{V_{i,\varepsilon}\subset E \ver... ...\varepsilon}=\{x\in E \vert p_i(x)<\varepsilon\}, i\in I,\varepsilon>0\right\}.$

Topologie de $ \mathcal {H}(U)$

Soit $ U$ un ouvert de $ \mathbb{C}$, on note $ \mathcal{C}(U)$ le sous espace vectoriel des applications continues de $ U$ dans $ \mathbb{C}$. Si $ K$ est un compact de $ U$ et si $ f\in\mathcal{C}(U)$, on pose

$\displaystyle \Vert f\Vert _K=\sup_{z\in K} \vert f(z)\vert.$

On munit $ \mathcal{C}(U)$ de la topologie définie par la famille des semi-normes $ \Vert.\Vert _K$, où $ K$ décrit les parties compactes de $ U$. Un système fondamental de voisinages de 0 est alors fourni par les ensembles

$\displaystyle V(K,\varepsilon)=\{f\in\mathcal{C}(U) \vert \Vert f\Vert _K<\varepsilon\}$

avec $ \varepsilon>0$ et $ K$ compact de $ U$.

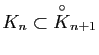Si $ (K_n)_{n\in\mathbb{N}}$ est une suite exhaustive de parties compactes de $ U$, c'est-à-dire une suite parties compactes telles que $ U=\cup_{n\in\mathbb{N}} K_n$ et $ K_n\subset\overset\circ K_{n+1}$ (il suffit par exemple de prendre $ K_n=\{z\in U \vert d(z,\mathbb{C}\setminus U)<\frac{1}{n}\}\cap D(0,n)$), la famille $ V(K_n,\frac{1}{n}), n\in\mathbb{N}^*,$ forme clairement un système fondamental dénombrable de voisinage de 0, la topologie définie par les semi-normes $ \Vert.\Vert _K$, où $ K$ décrit les parties compactes de $ U$ est donc une topologie métrisable et si $ f,g\in\mathcal{C}(U)$

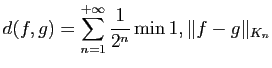
$\displaystyle d(f,g)=\sum_{n=1}^{+\infty} \frac{1}{2^n}\min{1,\Vert f-g\Vert _{K_n}}$

définit une distance compatible avec cette topologie.

Cette topologie est appelée topologie de la convergence uniforme sur tout compact de $ U$. Rappelons que $ \mathcal{C}(U)$, munit de cette topologie est complet.

Nous allons maintenant traduire les propriétés des suite de fonctions holomorphes que nous avons obtenues dans le théorème de Weierstraß en termes topologiques sur le sous espace vectoriel $ \mathcal {H}(U)$ de $ \mathcal{C}(U)$ constitué des fonctions holomorphes sur $ U$.

Théorème 24   Le sous espace $ \mathcal {H}(U)$ de $ \mathcal{C}(U)$ est fermé dans $ \mathcal{C}(U)$ et pour tout $ j\in\mathbb{N}$, l'application $ f\mapsto f^{(j)}$ de $ \mathcal {H}(U)$ dans lui-même est continue.

Le théorème d'Ascoli donne une caractérisation des parties compactes de $ \mathcal{C}(U)$. Nous allons nous intéresser maintenant aux parties compactes de $ \mathcal {H}(U)$.

Rappelons qu'une partie $ \mathcal{P}$ de $ \mathcal{C}(U)$ est bornée si et seulement si pour toute partie compacte $ K$ de $ U$, il existe une constante $ M_K$ telle que pour toute $ f\in\mathcal{P}$ on ait $ \Vert f\Vert _K<M_K$.

On déduit alors aisément des inégalités de Cauchy la proposition suivante :

Proposition 11   Soit $ K$ un compact de $ U$, $ r>0$ un nombre réel tel que pour tout $ a\in K$ le disque fermé $ \overline{D(a,r)}$ soit contenu dans $ U$ et $ X=\cup_{a\in K}\overline{D(a,r)}$. Alors, pour tout $ k\in\mathbb{N}$ et toute $ f\in\mathcal{H}(U)$, on a

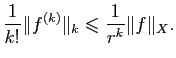
$\displaystyle \frac{1}{k!}\Vert f^{(k)}\Vert _k\leqslant \frac{1}{r^k}\Vert f\Vert _X.$

En particulier si $ \mathcal{P}$ est une partie bornée de $ \mathcal {H}(U)$, il en est de même de $ \{f^{(j)}, f\in\mathcal{P}\}$ pour tout $ j\in\mathbb{N}$.

On dit qu'une partie $ \mathcal{P}$ de $ \mathcal{C}(U)$ est équicontinue en un point $ z_0$ de $ U$ si et seulement si pour tout $ \varepsilon>0$ il existe $ \eta>0$ tel que pour toute $ f\in\mathcal{P}$ et tout $ z\in U$ tel que $ \vert z-z_0\vert<\eta$ on a $ \vert f(z)-f(z_0)\vert<\varepsilon$. La partie $ \mathcal{P}$ est équicontinue sur $ U$ si et seulement si elle est équicontinue en tout point de $ U$.

Ces définitions étant précisées nous pouvons rappeler l'énoncé du Théorème d'Ascoli.

Théorème 25 (d'Ascoli)   Pour qu'une partie $ \mathcal{P}$ de $ \mathcal{C}(U)$ soit relativement compacte pour la topologie de la convergence uniforme sur tout compact de $ U$ il suffit que $ \mathcal{P}$ soit équicontinue et bornée.

Le théorème de Montel va prouver qu'en raison des inégalités de Cauchy la caractérisation des parties compactes de $ \mathcal {H}(U)$ est plus simple que celle des parties compactes de $ \mathcal{C}(U)$ et comparable à la situation de la dimension finie.

Théorème 26 (de Montel)   Pour qu'une partie $ \mathcal{P}$ de $ \mathcal {H}(U)$ soit relativement compacte pour la topologie de la convergence uniforme sur tout compact de $ U$ il faut et il suffit que $ \mathcal{P}$ soit bornée.

Démonstration : Montrons tout d'abord la condition nécessaire. Raisonnons par l'absurde et supposons que $ \mathcal{P}$ n'est pas bornée. Il existe alors un compact $ K$ de $ U$ tel que, pour tout $ n\in\mathbb{N}$, il existe une fonction $ f_n\in\mathcal{P}$ telle que $ \Vert f_n\Vert\geqslant n$ et nous obtenons ainsi une suite de fonctions de $ \mathcal{P}$ qui ne possède aucune sous suite convergeant uniformément sur $ K$. La partie $ \mathcal{P}$ n'est donc pas relativement compacte dans $ \mathcal {H}(U)$.

Pour la condition suffisante, il suffit, par le Théorème d'Ascoli, de vérifier que si $ \mathcal{P}$ est bornée elle est aussi équicontinue. Supposons que $ \mathcal{P}$ est bornée et prouvons que $ \mathcal{P}$ est équicontinue au voisinage de tout point $ z_0$ de $ U$. Soient $ D=D(z_0,R)$ et $ \widetilde{D}=D(z_0,R+\delta)$, $ \delta>0$, deux disques de centre $ z_0$ tels que $ D\subset\subset\widetilde{D}\subset\subset U$. Grâce aux inégalités de Cauchy, pour toute $ f\in\mathcal{H}(U)$, on a

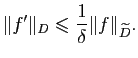
$\displaystyle \Vert f'\Vert _D\leqslant\frac{1}{\delta}\Vert f\Vert _{\widetilde{D}}.$

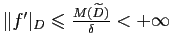Notons $ =\sup_{f\in\mathcal{P}} \Vert f\Vert _{\widetilde{D}}$. Alors, pour toute $ f\in\mathcal{P}$, on a $ \Vert f'\vert _D\leqslant\frac{M(\widetilde{D})}{\delta}<+\infty$, puisque $ \mathcal{P}$ est bornée.

Si $ z$ et $ z'$ sont deux points de $ D$ et si $ t\in[0,1]$ alors $ tz+(1-t)z'\in D$ car $ D$ est convexe. Pour $ f\in\mathcal{P}$, posons $ \varphi(t)=f(tz+(1-t)z')$, alors $ \varphi$ est de classe $ \mathcal {C}^1$ sur $ U$ et $ \varphi'(t)=(z-z')f'(tz+(1-t)z')$, de plus par le Théorème des accroissements finis

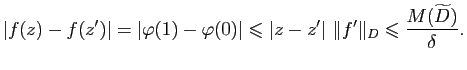
$\displaystyle \vert f(z)-f(z')\vert=\vert\varphi(1)-\varphi(0)\vert\leqslant \vert z-z'\vert \Vert f'\Vert _D\leqslant \frac{M(\widetilde{D})}{\delta}.$

On en déduit que $ f$ est lipschitzienne et que on remarque que la constante de Lipschitz ne dépend pas du choix de $ f$ dans $ \mathcal{P}$, par conséquent $ \mathcal{P}$ est équicontinue sur $ D$.$ \square$

Théorème de la représentation conforme de Riemann

Le but de cette section est de prouver que tout domaine étoilé de $ \mathbb{C}$ distinct de $ \mathbb{C}$ est biholomorphe au disque unité. Il s'agit d'un cas particulier du Théorème de la représentation conforme de Riemann qui affirme que tout domaine simplement connexe de $ \mathbb{C}$, c'est-à-dire sans trou ou plus précisément tel que son complémentaire ne possède aucune composante connexe bornée, distinct de $ \mathbb{C}$ est biholomorphe au disque unité.

On note $ D=D(0,1)$ le disque de centre 0 et de rayon $ 1$ de $ \mathbb{C}$.

Remarquons que $ \mathbb{C}$, bien qu'homéomorphe à $ D$ (par l'application $ z\mapsto \frac{z}{1+\vert z\vert}$), n'est par biholomorphe à $ D$. En effet si $ f$ est une application holomorphe de $ \mathbb{C}$ dans $ D$, $ f$ est bornée et donc constante par le Théorème de Liouville et par conséquent elle ne peut pas être injective.

Commençons par démontrer quelques propriétés des applications holomorphes de $ D$ dans $ D$. Si $ a\in\mathbb{C}$, on pose $ \varphi_a(z)=\frac{z-a}{1-\overline{a}z}$. Notons que si $ a\in D$, la fonction $ \varphi_a$ est définie et holomorphe sur $ D$.

Proposition 12   Une application $ \varphi$ de $ D$ dans $ D$ est un automorphisme de $ D$, c'est-à-dire une application bijective et biholomorphe de $ D$ dans lui-même, si et seulement si il existe $ a\in D$ tel que $ \varphi=\lambda\varphi_a$ avec $ \vert\lambda\vert=1$.

Démonstration : Montrons tout d'abord que $ \varphi_a(D)\subset D$. Pour $ z=\mathrm{e}^{\mathrm{i}t}$, $ t\in\mathbb{R}$ on a

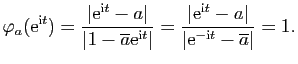
$\displaystyle \varphi_a(\mathrm{e}^{\mathrm{i}t})=\frac{\vert\mathrm{e}^{\mathr... ...e}^{\mathrm{i} t}-a\vert}{\vert\mathrm{e}^{-\mathrm{i}t}-\overline{a}\vert}=1.$

Par le principe du maximum on a donc $ \varphi_a(D)\subset D$.

Remarquons que $ \varphi_a\circ\varphi_{-a}=\mathrm{Id}$, donc par le théorème d'inversion locale $ \varphi_a$ est un automorphisme de $ D$, de plus $ \varphi_a(a)=0$.

Soit $ g$ un automorphisme de $ D$, on se ramène au cas où $ g(0)=0$ en remplaçant $ g$ par $ h=\varphi_{g(0)}\circ g$. On peut donc appliquer le Lemme de Schwarz à $ h$ et à $ h^{-1}$, on obtient ainsi pour tout $ z\in D$, $ \vert h(z)\vert\leqslant \vert z\vert\leqslant \vert h(z)\vert$, soit $ \vert h(z)\vert=\vert z\vert$ et encore une fois par le Lemme de Schwarz $ h(z)=\lambda z$ avec $ \vert\lambda\vert=1$.

Si $ g(0)=a$, on a donc $ \varphi_a\circ g(z)=\lambda z$ avec $ \vert\lambda\vert=1$, d'où

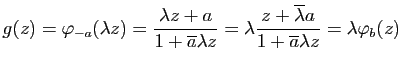
$\displaystyle g(z)=\varphi_{-a}(\lambda z)=\frac{\lambda z+a}{1+\overline{a}\la... ...ambda\frac{z+\overline{\lambda} a}{1+\overline{a}\lambda z}=\lambda\varphi_b(z)$

avec $ b=-a\overline{\lambda}$.$ \square$

Lemme 4   Soit $ f$ une fonction holomorphe dans $ D$ non injective et vérifiant $ f(D)\subset D$, alors $ \vert f'(0)\vert<1$

Démonstration : Posons $ a=f(0)$, alors la fonction $ g=\varphi_a\circ f$ est non injective et vérifie $ g(D)\subset D$ et $ g(0)=0$. En appliquant le Lemme de Schwarz à $ g$ on obtient $ \vert g'(0)\vert<1$ (si on avait $ \vert g'(0)\vert=1$, on aurait $ g(z)=\lambda z$ avec $ \vert\lambda\vert=1$ et $ g$ serait injective), soit $ \vert\varphi_a'(a)f'(0)<1$, c'est-à-dire $ \frac{1}{1-\vert a\vert^2}\vert f'(0)\vert<1$ et ainsi $ \vert f'(0)\vert<1-\vert a\vert^2<1$.$ \square$

Théorème 27   Soit $ U$ un ouvert connexe de $ \mathbb{C}$ distinct de $ \mathbb{C}$. On suppose que pour tout fonction $ f$ holomorphe sur $ U$, ne s'annulant pas sur $ U$, il existe une fonction $ g$ holomorphe sur $ U$ telle que $ f=g^2$. Alors l'ouvert $ U$ est biholomorphe à $ D$.

Démonstration : On désigne par $ \mathcal{P}$ le sous ensemble de $ \mathcal {H}(U)$ constitué des applications $ f$ injectives de $ U$ dans $ D$. La démonstration se divise en trois grandes étapes

Première étape. Montrons que $ \mathcal{P}$ n'est pas vide. Nous allons construire une application $ g$ holomorphe, injective sur $ U$ dont l'image $ g(U)$ évite un disque fermé $ \overline{D(c,r)}$ de centre $ c$ et de rayon $ r>0$, ainsi pour tout $ z\in U$ nous aurons $ \vert g(z)-c\vert>r$ et en posant $ f(z)=\frac{r}{g(z)-c}$ nous définirons une fonction holomorphe sur $ U$, injective et telle que $ \vert f(z)\vert<1$ pour tout $ z\in U$, soit $ f(U)\subset D$. Une telle fonction $ f$ sera un élément de $ \mathcal{P}$.

Fixons $ a\in\mathbb{C}\setminus U$, la fonction $ z\mapsto z-a$ est holomorphe dans $ U$ et ne s'annule pas, il existe donc une fonction $ g$ holomorphe dans $ U$ telle que $ (g(z))^2=z-a$ pour tout $ z\in U$. Notons que $ g$ ainsi définie est injective puisque, si $ z,w\in U$, $ g(z)=g(w)$ alors en élevant au carré $ z-a=w-a$, soit $ z=w$. Notons également que si $ g(z)=-g(w)$ alors en élevant au carré on obtient encore $ z-a=w-a$, soit $ z=w$. Puisque la fonction $ g$ ne s'annule pas on déduit de cette dernière assertion que si $ x\in g(U)$ alors $ -x\notin g(U)$.

Par ailleurs l'application $ g$ est holomorphe sur $ U$, qui est connexe, et non constante donc ouverte et par conséquent il existe $ b\in\mathbb{C}$ et $ r>0$ tel que le disque fermé $ \overline{D(b,r)}$ soit contenu dans $ g(U)$. La remarque précédente implique donc que $ g(U)\cap\overline{D(-b,r)}=\emptyset$ et donc $ c=-b$ convient et nous avons construit la fonction $ g$ cherchée.

Figure 12: Le domaine $ g(U)$ ne rencontre ni l'origine, ni $ D(-b,r)$.
\includegraphics[width=6cm]{conforme}

Deuxième étape. Montrons que si $ z_0$ est un point de $ U$ et si $ f\in\mathcal{P}$ n'est pas surjective, il existe $ h\in\mathcal{P}$ telle que $ \vert h'(z_0)\vert>\vert f'(z_0)\vert$.

Puisque $ f$ n'est pas surjective, il existe $ a\in D\setminus f(U)$ et en composant par l'automorphisme $ \varphi_a$ de $ D$ nous obtenons une application $ \varphi_a\circ f\in\mathcal{P}$ qui ne s'annule pas sur $ U$. Notons $ \sigma$ l'application de $ \mathbb{C}$ dans $ \mathbb{C}$ définie par $ \sigma(z)=z^2$. Par hypothèse il existe alors une fonction $ g$ holomorphe dans $ U$ telle que $ \sigma\circ=\varphi_a\circ f$. L'application $ g$ est clairement injective et satisfait $ g(U)\subset D$. Posons $ b=g(z_0)$ et $ h=\varphi_b\circ g$. La fonction $ h$ est clairement un élément de $ \mathcal{P}$ et $ h(z_0)=0$. Posons $ \psi=\varphi_{-a}\circ\sigma\circ\varphi_{-b}$, alors

$\displaystyle f=\varphi_{-a}\circ\sigma\circ g=\varphi_{-a}\circ\sigma\circ\varphi_{-b}\circ\varphi_b\circ g=\psi\circ h$

et $ f'(z_0)=\psi'(0)h'(z_0)$.

L'application $ \psi$ est holomorphe, non injective de $ D$ dans $ D$, car $ \sigma$ n'est pas injective, donc par le Lemme 4 on a $ \psi'(0)<1$. De plus $ f$ étant injective, $ f'(z_0)\neq 0$ et par conséquent $ \vert h'(z_0)\vert>\vert f'(z_0)\vert$.

Troisième étape. Soit $ z_0$ un point de $ U$, montrons qu'il existe $ f\in\mathcal{P}$ telle que
$ \vert f'(z_0)\vert=\sup\{\vert g'(z_0)\vert, g\in\mathcal{P}\}$ et qu'une telle fonction $ f$ définit un isomorphisme de $ U$ sur $ D$.

L'ensemble $ \mathcal{P}$ est une partie bornée de $ \mathcal {H}(U)$ puisque si $ f\in\mathcal{P}$ alors $ f(U)\subset D$ (en effet pour tout $ f\in\mathcal{P}$ et tout $ z\in U$, on a $ \vert f(z)\vert<1$). On déduit alors des inégalités de Cauchy que $ M=\sup\{\vert f'(z_0)\vert, f\in\mathcal{P}\}<+\infty$, de plus les élément de $ \mathcal{P}$ étant des fonctions holomorphes, injectives on a $ M>0$. On peut donc considérer une suite $ (f_n)_{n\in\mathbb{N}}$ d'éléments de $ \mathcal{P}$ telle que la suite de nombres réels $ (\vert f'_n(z_0)\vert)_{n\in\mathbb{N}}$ converge vers $ M$. Puisque $ \mathcal{P}$ est bornée, donc relativement compacte par le Théorème de Montel, quitte à extraire, on peut supposer que la suite $ (f_n)_{n\in\mathbb{N}}$ converge uniformément sur tout compact de $ U$ vers une fonction $ f$ holomorphe sur $ U$ et telle que $ \vert f'(z_0)\vert=M$ par le Théorème de Weierstraß. Comme $ M\neq 0$, la fonction $ f$ n'est pas constante et le Théorème 17 implique que $ f$ est injective puisque les $ f_n$ le sont.

Montrons que $ f(U)\subset D$, ce qui implique que $ f\in\mathcal{P}$. Par définition des éléments de $ \mathcal{P}$, pour tout $ n\in\mathbb{N}$, $ f_n(U)\subset D$ et par conséquent en tant que limite de la suite $ (f_n)_{n\in\mathbb{N}}$ la fonction $ f$ vérifie $ f(U)\subset\overline{D}$, mais la fonction $ f$ n'étant pas constante elle est ouverte et donc $ f(U)\subset D$.

Puisque $ f\in\mathcal{P}$ et $ \vert f'(z_0)\vert=M$, il résulte de la seconde étape que $ f$ qui est une application holomorphes injective de $ U$ dans $ D$ est de plus surjective. Le Théorème d'inversion locale prouve alors que $ f$ est un isomorphisme de $ U$ sur $ D$.$ \square$

Proposition 13   Soit $ U$ un ouvert connexe de $ \mathbb{C}$ tel que toute fonction holomorphe sur $ U$ admet une primitive $ U$. Alors si $ f$ est une fonction holomorphe sur $ U$ qui ne s'annule pas sur $ U$, il existe une fonction $ g$ holomorphe sur $ U$ telle que

$\displaystyle \mathrm{e}^g=f.$

De plus pour tout $ k\in\mathbb{N}^*$, il existe une fonction $ h$ holomorphe sur $ U$ telle que $ h^k=f$.

Démonstration : Supposons qu'il existe une fonction $ g$ holomorphe sur $ U$ telle que $ \mathrm{e}^g=f$, alors $ g'f=f'$. Puisque $ f$ ne s'annule pas la fonction $ \frac{f'}{f}$ est holomorphe sur $ U$ et par hypothèse possède une primitive dans $ U$. Soient $ z_0$ un point de $ U$ et $ w\in\mathbb{C}$ tel que $ \mathrm{e}^w=f(z_0)$, notons $ g$ la primitive de $ \frac{f'}{f}$ qui prend la valeur $ w$ en $ z_0$, elle vérifie $ \mathrm{e}^g=f$.

Pour $ k\in\mathbb{N}^*$, la fonction $ h=\mathrm{e}^\frac{g}{k}$ est holomorphe sur $ U$ et vérifie $ h^k=f$.$ \square$

Le Théorème 27 et la Proposition 13 donnent le résultat suivant :

Corollaire 14   Tout ouvert connexe de $ \mathbb{C}$ sur lequel toute fonction holomorphe admet une primitive, en particulier tout ouvert convexe ou étoilé, distinct de $ \mathbb{C}$ est biholomorphe au disque unité.


Section : Cours
Avant : Théorie de Cauchy globale
Après : Entraînement


         © UJF Grenoble, 2011                              Mentions légales