Ce chapitre ne traite que des espaces finiment engendrés.
Définition 7
On dit qu'un espace vectoriel est finiment engendré s'il est
engendré par un nombre fini de vecteurs.
Voici deux observations symétriques.
- Si on ajoute un vecteur à une famille génératrice, alors elle ne
peut plus être libre.
En effet, tout vecteur ajouté est forcément combinaison linéaire
des précédents, ce qui n'est pas possible dans une famille libre.
- Si on enlève un vecteur à une famille libre, alors elle ne
peut plus être génératrice.
En effet, le vecteur que l'on vient d'enlever n'est pas combinaison
linéaire des autres, donc il n'est pas dans l'espace engendré par
les autres.
Définition 8
On appelle base toute famille à la fois génératrice et
libre.
Nous avons déjà rencontré plusieurs bases.
Les familles
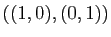 et
et
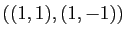 sont deux bases de
sont deux bases de
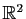 .
Dans
.
Dans
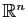 ,
,
est une base, que l'on appelle la base canonique.
La proposition suivante nous permettra de parler
de bases en étant assurés de leur existence. Sa démonstration
montrera aussi
qu'on peut extraire une base de toute famille génératrice.
Proposition 4
Dans un espace vectoriel, différent de 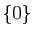 et
finiment engendré, il existe une base.
et
finiment engendré, il existe une base.
Démonstration : Soit
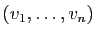 une famille génératrice de
l'espace. Puisque cet espace est différent de
une famille génératrice de
l'espace. Puisque cet espace est différent de 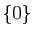 ,
au moins un des
,
au moins un des 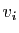 est non nul. Si
est non nul. Si 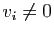 ,
, 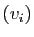 est une famille libre. Parmi les sous-familles,
extraites de
est une famille libre. Parmi les sous-familles,
extraites de
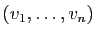 ,
considérons celles qui sont des familles libres, et choisissons parmi
elles une famille libre ayant le plus grand nombre d'éléments.
Notons
,
considérons celles qui sont des familles libres, et choisissons parmi
elles une famille libre ayant le plus grand nombre d'éléments.
Notons  ce nombre d'éléments maximal. On peut renuméroter
les
ce nombre d'éléments maximal. On peut renuméroter
les 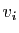 de sorte que
de sorte que
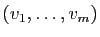 soit une famille
libre. Puisque le nombre
soit une famille
libre. Puisque le nombre  est maximal, les
vecteurs
est maximal, les
vecteurs
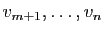 sont des combinaisons linéaires de
sont des combinaisons linéaires de
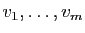 . Donc tout vecteur est combinaison linéaire de
. Donc tout vecteur est combinaison linéaire de
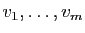 . Donc
. Donc
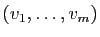 est à la fois
génératrice et libre : c'est une base.
est à la fois
génératrice et libre : c'est une base.
Le résultat principal de cette section est le suivant.
Théorème 3
Dans un espace vectoriel, différent de 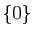 et
finiment engendré, toutes les bases ont le
même nombre d'éléments.
et
finiment engendré, toutes les bases ont le
même nombre d'éléments.
Démonstration : La partie difficile de la démonstration réside dans le lemme
suivant.
Lemme 1
Si un espace possède une famille génératrice à  éléments, alors toute famille de
éléments, alors toute famille de 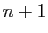 éléments est liée.
éléments est liée.
Admettons ce lemme pour l'instant. Si deux bases
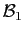 et
et
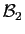 ont
pour cardinaux
ont
pour cardinaux 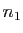 et
et 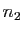 , alors
, alors
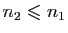 d'après le lemme,
car
d'après le lemme,
car
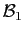 est génératrice et
est génératrice et
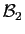 est libre.
De façon
symétrique, puisque
est libre.
De façon
symétrique, puisque
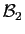 est génératrice et
est génératrice et
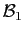 est libre,
est libre,
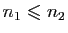 . Donc
. Donc 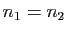 , et le
théorème est démontré.
La démonstration du lemme se fait par récurrence sur le cardinal
de la famille génératrice. Supposons que l'espace admette une
famille génératrice à un seul élément
, et le
théorème est démontré.
La démonstration du lemme se fait par récurrence sur le cardinal
de la famille génératrice. Supposons que l'espace admette une
famille génératrice à un seul élément  . Soit l'espace
est une droite vectorielle soit il ne contient que le vecteur nul :
tous les vecteurs sont proportionnel à
. Soit l'espace
est une droite vectorielle soit il ne contient que le vecteur nul :
tous les vecteurs sont proportionnel à  . Deux
vecteurs quelconques s'écrivent
. Deux
vecteurs quelconques s'écrivent
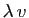 et
et 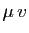 , pour un
certain couple de réels
, pour un
certain couple de réels
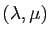 , et ils
sont liés car, soit au moins l'un des deux est nul, soit chacun est
proportionnel à l'autre (cf. proposition 3).
, et ils
sont liés car, soit au moins l'un des deux est nul, soit chacun est
proportionnel à l'autre (cf. proposition 3).
Supposons maintenant que le résultat du lemme soit vrai pour une
famille génératrice de  vecteurs. Nous voulons passer au rang
vecteurs. Nous voulons passer au rang
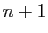 . Considérons un espace engendré par les vecteurs
. Considérons un espace engendré par les vecteurs
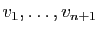 et une famille de
et une famille de 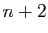 vecteurs
vecteurs
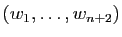 . Nous devons montrer qu'elle est liée.
. Nous devons montrer qu'elle est liée.
Chacun des 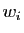 est combinaison linéaire
des
est combinaison linéaire
des 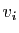 . Dans ces combinaisons linéaires, isolons la partie
concernant
. Dans ces combinaisons linéaires, isolons la partie
concernant 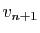 .
.
où 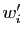 appartient au sous-espace engendré par
appartient au sous-espace engendré par
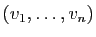 . Si tous les
. Si tous les 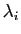 sont nuls, cela
signifie que les
sont nuls, cela
signifie que les 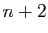 vecteurs
vecteurs 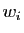 sont tous dans le
sous-espace engendré par
sont tous dans le
sous-espace engendré par
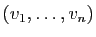 . La famille est donc
liée, par application de l'hypothèse de
récurrence. Supposons maintenant que l'un des
. La famille est donc
liée, par application de l'hypothèse de
récurrence. Supposons maintenant que l'un des 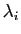 est non
nul. Quitte à changer l'ordre des vecteurs, nous pouvons
supposer
est non
nul. Quitte à changer l'ordre des vecteurs, nous pouvons
supposer
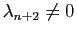 .
Alors
.
Alors 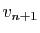 s'écrit :
s'écrit :
Donc,
soit,
Les 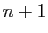 vecteurs
vecteurs
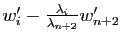 ,
qui appartiennent à l'espace engendré
par
,
qui appartiennent à l'espace engendré
par
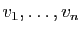 , sont liés, d'après l'hypothèse de
récurrence. Donc il existe
, sont liés, d'après l'hypothèse de
récurrence. Donc il existe
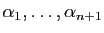 non tous
nuls, tels que
non tous
nuls, tels que
Ceci entraîne que
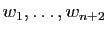 sont liés, ce qui
achève la démonstration du lemme.
sont liés, ce qui
achève la démonstration du lemme.
Le théorème 3 permet de définir rigoureusement la
notion de dimension.
Définition 9
Soit  un espace vectoriel, différent de
un espace vectoriel, différent de 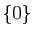 et
finiment engendré.
On appelle dimension de
et
finiment engendré.
On appelle dimension de  le nombre d'éléments commun
à toute base de
le nombre d'éléments commun
à toute base de  .
.
On étend la définition à un espace vectoriel contenant seulement
le vecteur nul, en convenant que sa dimension est 0.
Les espaces de dimension 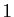 sont les droites vectorielles, ceux de
dimension
sont les droites vectorielles, ceux de
dimension 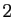 sont les plans vectoriels. L'espace
sont les plans vectoriels. L'espace
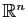 est de
dimension
est de
dimension  . Les
sous-espaces de dimension
. Les
sous-espaces de dimension 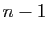 dans
dans
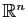 s'appellent les hyperplans de
s'appellent les hyperplans de
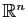 .
Si on connaît la dimension de l'espace, il est facile
de vérifier si une famille de vecteurs est ou non une base,
grâce au théorème suivant.
.
Si on connaît la dimension de l'espace, il est facile
de vérifier si une famille de vecteurs est ou non une base,
grâce au théorème suivant.
Théorème 4
Dans un espace vectoriel de dimension  :
:
- toute famille libre a au plus
 éléments,
éléments,
- toute famille libre de
 éléments est une base,
éléments est une base,
- toute famille génératrice a au moins
 éléments,
éléments,
- toute famille génératrice de
 éléments est une base.
éléments est une base.
Démonstration : Le premier point découle directement du lemme 1 :
toute famille ayant au moins 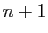 vecteurs est liée.
vecteurs est liée.
Pour le second point, soit
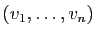 une famille libre,
et
une famille libre,
et  un vecteur quelconque de l'espace. D'après le premier point,
un vecteur quelconque de l'espace. D'après le premier point,
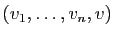 est
forcément liée : il existe une combinaison linéaire nulle, dont
les coefficients ne sont pas tous nuls. Le
coefficient de
est
forcément liée : il existe une combinaison linéaire nulle, dont
les coefficients ne sont pas tous nuls. Le
coefficient de  dans cette combinaison linéaire ne peut pas
être nul, car
dans cette combinaison linéaire ne peut pas
être nul, car
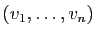 est libre. Donc
est libre. Donc  est
combinaison linéaire de
est
combinaison linéaire de
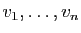 . Donc
. Donc
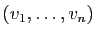 est génératrice : c'est une base.
est génératrice : c'est une base.
Pour le troisième point si une famille génératrice avait 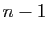 éléments, alors par le lemme 1 toute famille de
éléments, alors par le lemme 1 toute famille de
 éléments serait liée, et donc aucune base ne pourrait avoir
éléments serait liée, et donc aucune base ne pourrait avoir
 éléments.
éléments.
Le quatrième point découle de la démonstration de la proposition
4. Si une famille est génératrice, une de ses
sous-familles est une base. Si la famille génératrice a  éléments, la base extraite ne peut être que la famille elle-même.
éléments, la base extraite ne peut être que la famille elle-même.  Comme il est naturel, tout sous-espace vectoriel d'une espace
vectoriel de dimension finie est lui-même de dimension finie.
Comme il est naturel, tout sous-espace vectoriel d'une espace
vectoriel de dimension finie est lui-même de dimension finie.
Proposition 5
Soit  un espace vectoriel de dimension
un espace vectoriel de dimension  . Tout sous-espace
vectoriel de
. Tout sous-espace
vectoriel de  est de dimension finie, inférieure ou égale à
est de dimension finie, inférieure ou égale à  .
.
Démonstration : Soit  un sous-espace vectoriel de
un sous-espace vectoriel de  . Toute famille libre
d'éléments de
. Toute famille libre
d'éléments de  est aussi une famille libre dans
est aussi une famille libre dans  , elle a
donc moins de
, elle a
donc moins de  éléments d'après le point 1 du
théorème 4. Considérons une famille libre
d'éléments de
éléments d'après le point 1 du
théorème 4. Considérons une famille libre
d'éléments de  , de longueur maximale.
Soit
, de longueur maximale.
Soit
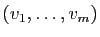 cette famille. Soit
cette famille. Soit  un vecteur quelconque
de
un vecteur quelconque
de  . La famille
. La famille
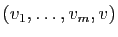 ne peut pas être libre. Elle
est donc liée, donc
ne peut pas être libre. Elle
est donc liée, donc  est combinaison linéaire de
est combinaison linéaire de
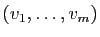 . La famille
. La famille
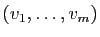 est donc
génératrice : c'est une base de
est donc
génératrice : c'est une base de  .
.  La dimension de l'espace engendré par une famille de vecteurs est le
rang de cette famille.
La dimension de l'espace engendré par une famille de vecteurs est le
rang de cette famille.
Définition 10
On appelle rang d'une famille de vecteurs la dimension de
l'espace vectoriel qu'elle engendre.
Les observations suivantes sont des conséquences faciles du théorème
4 :
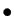
- le rang d'une famille de
 vecteurs est au plus
vecteurs est au plus 
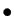
- le rang d'une famille de
 vecteurs est
vecteurs est  si et seulement si cette
famille est libre
si et seulement si cette
famille est libre
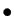
- le rang d'une famille de
 vecteurs est
vecteurs est  si et seulement si cette
famille est une base de l'espace vectoriel qu'elle engendre.
si et seulement si cette
famille est une base de l'espace vectoriel qu'elle engendre.
Nous verrons plus loin un moyen systématique
pour déterminer le rang d'une famille de vecteurs, et en extraire
une base de l'espace engendré.
L'intérêt des bases est qu'elles permettent d'identifier tout
espace de dimension finie à
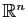 , grâce à la notion de
coordonnées.
, grâce à la notion de
coordonnées.
Démonstration : Comme la famille
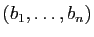 est génératrice,
est génératrice,  s'exprime comme combinaison linéaire de
s'exprime comme combinaison linéaire de
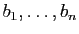 , d'où
l'existence. Pour l'unicité, supposons
que deux combinaisons linéaires soient
égales.
, d'où
l'existence. Pour l'unicité, supposons
que deux combinaisons linéaires soient
égales.
Ceci implique
donc 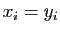 , pour tout
, pour tout
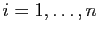 , puisque
, puisque
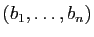 est une famille libre.
est une famille libre. 
Les réels
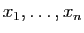 sont les coordonnées de
sont les coordonnées de  dans
la base
dans
la base
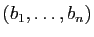 .
.
Par exemple, les coordonnées de 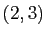 dans la base
dans la base
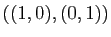 sont
sont 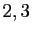 . Dans la base
. Dans la base
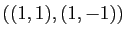 , ses coordonnées sont
, ses coordonnées sont
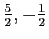 . Les coordonnées de
. Les coordonnées de
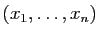 dans la base canonique de
dans la base canonique de
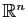 sont
sont
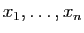 .
Le théorème suivant, dit «théorème de la base incomplète»
montre qu'on peut fabriquer une base
en complétant une famille libre par des
éléments d'une famille génératrice.
.
Le théorème suivant, dit «théorème de la base incomplète»
montre qu'on peut fabriquer une base
en complétant une famille libre par des
éléments d'une famille génératrice.
Démonstration : Appelons «famille complétée», soit la famille
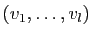 ,
soit une famille du type
,
soit une famille du type
avec
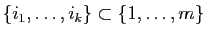 . On considère
l'ensemble (fini et non vide)
de toutes les familles complétées libres.
Dans cet ensemble, on choisit une
famille ayant le plus grand nombre possible
d'éléments. Soit
. On considère
l'ensemble (fini et non vide)
de toutes les familles complétées libres.
Dans cet ensemble, on choisit une
famille ayant le plus grand nombre possible
d'éléments. Soit 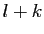 ce nombre maximal d'éléments.
On peut renuméroter
les
ce nombre maximal d'éléments.
On peut renuméroter
les 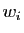 de sorte que
de sorte que
soit une famille libre. Puisque 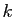 est maximal, pour
est maximal, pour
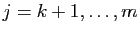 ,
,
est liée. Il s'ensuit que 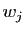 est combinaison linéaire de
est combinaison linéaire de
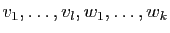 .
.
Mais comme
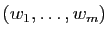 est
génératrice, tout vecteur de l'espace est combinaison linéaire
de
est
génératrice, tout vecteur de l'espace est combinaison linéaire
de
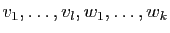 . Donc
. Donc
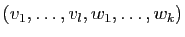 est une base.
est une base.
On utilise le théorème 6 le plus souvent
sous la forme affaiblie suivante.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
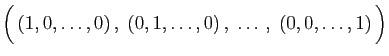
![]() vecteurs. Nous voulons passer au rang
vecteurs. Nous voulons passer au rang
![]() . Considérons un espace engendré par les vecteurs
. Considérons un espace engendré par les vecteurs
![]() et une famille de
et une famille de ![]() vecteurs
vecteurs
![]() . Nous devons montrer qu'elle est liée.
. Nous devons montrer qu'elle est liée.
![]() est combinaison linéaire
des
est combinaison linéaire
des ![]() . Dans ces combinaisons linéaires, isolons la partie
concernant
. Dans ces combinaisons linéaires, isolons la partie
concernant ![]() .
.
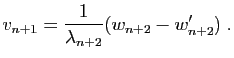
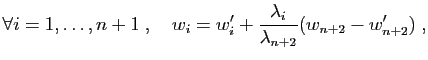
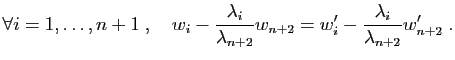
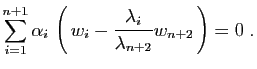
![]() une famille libre,
et
une famille libre,
et ![]() un vecteur quelconque de l'espace. D'après le premier point,
un vecteur quelconque de l'espace. D'après le premier point,
![]() est
forcément liée : il existe une combinaison linéaire nulle, dont
les coefficients ne sont pas tous nuls. Le
coefficient de
est
forcément liée : il existe une combinaison linéaire nulle, dont
les coefficients ne sont pas tous nuls. Le
coefficient de ![]() dans cette combinaison linéaire ne peut pas
être nul, car
dans cette combinaison linéaire ne peut pas
être nul, car
![]() est libre. Donc
est libre. Donc ![]() est
combinaison linéaire de
est
combinaison linéaire de
![]() . Donc
. Donc
![]() est génératrice : c'est une base.
est génératrice : c'est une base.
![]() éléments, alors par le lemme 1 toute famille de
éléments, alors par le lemme 1 toute famille de
![]() éléments serait liée, et donc aucune base ne pourrait avoir
éléments serait liée, et donc aucune base ne pourrait avoir
![]() éléments.
éléments.
![]() éléments, la base extraite ne peut être que la famille elle-même.
éléments, la base extraite ne peut être que la famille elle-même. ![]() Comme il est naturel, tout sous-espace vectoriel d'une espace
vectoriel de dimension finie est lui-même de dimension finie.
Comme il est naturel, tout sous-espace vectoriel d'une espace
vectoriel de dimension finie est lui-même de dimension finie.
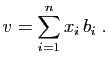
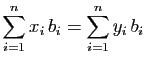
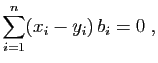
![]() sont les coordonnées de
sont les coordonnées de ![]() dans
la base
dans
la base
![]() .
.
![]() dans la base
dans la base
![]() sont
sont ![]() . Dans la base
. Dans la base
![]() , ses coordonnées sont
, ses coordonnées sont
![]() . Les coordonnées de
. Les coordonnées de
![]() dans la base canonique de
dans la base canonique de
![]() sont
sont
![]() .
Le théorème suivant, dit «théorème de la base incomplète»
montre qu'on peut fabriquer une base
en complétant une famille libre par des
éléments d'une famille génératrice.
.
Le théorème suivant, dit «théorème de la base incomplète»
montre qu'on peut fabriquer une base
en complétant une famille libre par des
éléments d'une famille génératrice.
![]() est
génératrice, tout vecteur de l'espace est combinaison linéaire
de
est
génératrice, tout vecteur de l'espace est combinaison linéaire
de
![]() . Donc
. Donc
![]() est une base.
est une base.![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales