Nous reprenons dans ce chapitre, de manière plus détaillée, la
théorie des espaces vectoriels de dimension finie. Dans la mesure
où il ne sera question que de vecteurs, abandonner
les flèches au-dessus de leurs écritures ne devrait pas
introduire de confusion.
Un espace vectoriel est un ensemble sur lequel sont définies
- une addition interne (on peut ajouter entre eux deux éléments de
l'ensemble) ;
- une multiplication externe (on peut multiplier un élément de
l'ensemble par un nombre réel).
Ces deux opérations doivent vérifier certaines
propriétés de compatibilité
qui sont listées dans la définition 1.
Définition 1
On dit que  est un espace vectoriel sur
est un espace vectoriel sur
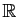 si
si  est muni d'une
addition et d'une multiplication externe vérifiant les
propriétés suivantes.
est muni d'une
addition et d'une multiplication externe vérifiant les
propriétés suivantes.
- Addition :
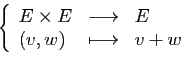
- Associativité :
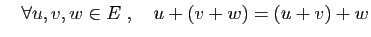
- Elément neutre :
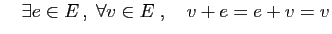
- Opposé :
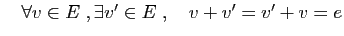
- Commutativité :
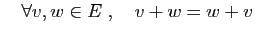
Ces propriétés font de 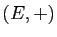 un groupe commutatif.
un groupe commutatif.
- Multiplication externe :
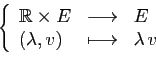
- 5.
- Associativité :
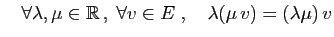
- 6.
- Elément neutre :
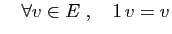
- 7.
- Distributivité (1) :
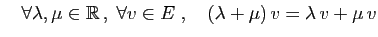
- 8.
- Distributivité (2) :
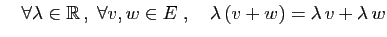
La proposition suivante nous autorisera à noter 0 l'élément
neutre pour l'addition (nous l'appellerons «vecteur nul»)
et 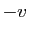 l'opposé de
l'opposé de  .
.
Proposition 1
Soit  un espace vectoriel.
un espace vectoriel.
- Le produit par le réel 0 d'un vecteur
 quelconque est
l'élément neutre pour l'addition :
quelconque est
l'élément neutre pour l'addition :
- Le produit par le réel
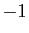 d'un vecteur
d'un vecteur  quelconque est
son opposé pour l'addition :
quelconque est
son opposé pour l'addition :
Démonstration : Notons (provisoirement) 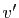 l'opposé de
l'opposé de  pour l'addition :
pour l'addition : 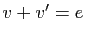 .
En utilisant les propriétés de la définition 1 :
.
En utilisant les propriétés de la définition 1 :
Ceci démontre le premier point. Pour le second, il suffit
d'écrire

L'exemple fondamental est l'ensemble des
 -uplets de réels :
-uplets de réels :
L'ensemble des  -uplets de réels (couples pour
-uplets de réels (couples pour 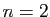 ,
triplets pour
,
triplets pour 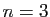 , ...), est muni de l'addition et
de la multiplication par un réel, coordonnée par coordonnée.
, ...), est muni de l'addition et
de la multiplication par un réel, coordonnée par coordonnée.
- Addition :
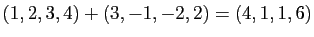
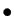
- Multiplication externe :
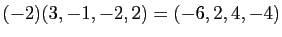
Le singleton contenant seulement le vecteur nul est un espace
vectoriel particulier.
L'associativité de l'addition permet d'écrire (sans parenthèses)
des combinaisons linéaires de vecteurs.
Il est inutile de s'inquiéter de la quantité de
propriétés à vérifier dans la définition
1. Dans tous les exemples que l'on rencontrera,
les opérations sont parfaitement naturelles et leurs propriétés
évidentes. On ne vérifie d'ailleurs jamais les
 propriétés de la définition 1. La raison pour
laquelle c'est inutile est que tous les espaces vectoriels que l'on
utilise sont des sous-espaces d'un espace vectoriel,
c'est-à-dire qu'ils sont des sous-ensembles, sur lesquels on
applique localement les opérations de l'espace entier.
propriétés de la définition 1. La raison pour
laquelle c'est inutile est que tous les espaces vectoriels que l'on
utilise sont des sous-espaces d'un espace vectoriel,
c'est-à-dire qu'ils sont des sous-ensembles, sur lesquels on
applique localement les opérations de l'espace entier.
Définition 3
Soit  un espace vectoriel et
un espace vectoriel et  un sous-ensemble non vide de
un sous-ensemble non vide de
 . On dit que
. On dit que  est un sous-espace vectoriel de
est un sous-espace vectoriel de  s'il est
un espace vectoriel pour l'addition et la multiplication externe de
s'il est
un espace vectoriel pour l'addition et la multiplication externe de  .
.
Observons que tout sous-espace vectoriel de  contient au moins le
vecteur nul.
La notion prend tout son intérêt grâce au théorème
suivant.
contient au moins le
vecteur nul.
La notion prend tout son intérêt grâce au théorème
suivant.
Démonstration : Parmi les 8 propriétés de la définition 1, celles
qui ne font intervenir que le
quantificateur 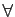 (associativités, commutativité,
distributivités), puisqu'elles sont vraies dans
(associativités, commutativité,
distributivités), puisqu'elles sont vraies dans  , restent vraies
dans
, restent vraies
dans  à cause de (1).
Il suffit donc de vérifier les
à cause de (1).
Il suffit donc de vérifier les 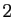 propriétés impliquant
une existence (élément neutre et opposé). Nous devons
démontrer que
propriétés impliquant
une existence (élément neutre et opposé). Nous devons
démontrer que  contient le vecteur nul, ainsi que l'opposé de
tout vecteur de
contient le vecteur nul, ainsi que l'opposé de
tout vecteur de  . D'après le premier point de la
proposition 1, le vecteur nul
s'écrit
. D'après le premier point de la
proposition 1, le vecteur nul
s'écrit 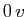 pour tout vecteur
pour tout vecteur  de
de  , donc pour tout vecteur
de
, donc pour tout vecteur
de  . Comme
. Comme  est non vide, le vecteur nul est donc dans
est non vide, le vecteur nul est donc dans  .
De même si
.
De même si  est un vecteur de
est un vecteur de  ,
alors son opposé, qui s'écrit
,
alors son opposé, qui s'écrit 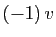 d'après le second point
de la proposition 1, est aussi dans
d'après le second point
de la proposition 1, est aussi dans  .
. 
Démonstration : Rappelons que  est un sous-espace vectoriel de
est un sous-espace vectoriel de  si et seulement si il
vérifie (1). L'équivalence entre (1)
et 2 est un exercice facile, laissé au lecteur. L'implication
3
si et seulement si il
vérifie (1). L'équivalence entre (1)
et 2 est un exercice facile, laissé au lecteur. L'implication
3
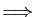 2 est évidente. Nous allons
démontrer la réciproque 2
2 est évidente. Nous allons
démontrer la réciproque 2
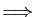 3, par
récurrence sur
3, par
récurrence sur  .
Notons
.
Notons 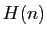 l'hypothèse de récurrence :
l'hypothèse de récurrence :
Le point 2 est 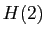 , et il implique
, et il implique 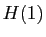 (cas
particulier
(cas
particulier 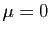 ). Supposons que
). Supposons que 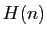 soit vrai. Soient
soit vrai. Soient
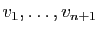
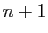 vecteurs de
vecteurs de  et
et
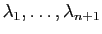
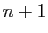 réels. Ecrivons
réels. Ecrivons
avec
Le vecteur  appartient à
appartient à  , par
, par 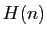 . La combinaison
linéaire
. La combinaison
linéaire
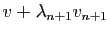 appartient à
appartient à  d'après
d'après 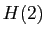 , d'où
le résultat.
, d'où
le résultat. 
Comme conséquence directe des théorèmes 1 ou bien
2, on vérifie facilement le résultat suivant.
Proposition 2
L'intersection de deux sous-espaces vectoriels est un sous-espace
vectoriel.
La réunion de deux sous-espaces vectoriels n'est pas un
espace vectoriel en général (pensez à deux droites distinctes).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
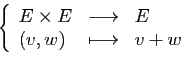
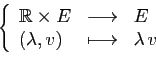
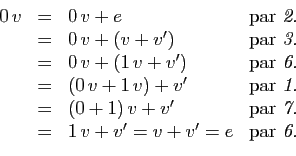
![]() -uplets de réels :
-uplets de réels :
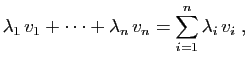
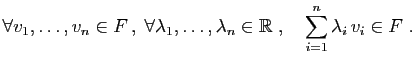
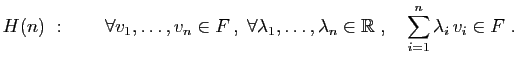
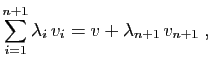
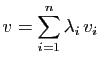
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales