Une courbe gauche est une courbe de
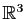 qui n'est pas plane. Dans cette partie, on considère les courbes paramétrées régulières gauches de classe
qui n'est pas plane. Dans cette partie, on considère les courbes paramétrées régulières gauches de classe 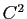 de la forme :
de la forme :
L'étude de l'allure locale est plus compliquée que pour les courbes planes. En effet, pour une courbe plane paramétrée régulière, il n'y a qu'une seule direction normale en chaque point de la courbe. Pour une courbe gauche, il y a tout un plan qui est orthogonal au vecteur tangent à la courbe en chaque point, ce qui complique un peu son étude et introduit une nouvelle notion, celle de torsion.
Courbure et normale principale
Dans le cas des courbes planes, le signe de la courbure algébrique est lié au sens de parcours de la courbe et à l'orientation du plan. Pour une courbe gauche, il n'est plus possible d'avoir un signe de courbure cohérent : intuitivement, quand on se promène sur la courbe, on ne peut pas de manière naturelle dire où est la droite, et où est la gauche. On ne définit donc pas de courbure algébrique, mais uniquement une courbure (qui est toujours positive).
Proposition 8
La courbure d'une courbe paramétrée régulière
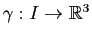 de classe
de classe 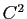 au point de paramètre
au point de paramètre 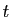 vaut :
vaut :
Démonstration : La preuve est similaire à celle pour les courbes planes.
Définition 12
Soit
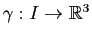 une courbe régulière paramétrée normale de classe
une courbe régulière paramétrée normale de classe 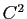 .
.
De même que pour les courbes planes, la dérivée seconde
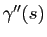 est orthogonale à
est orthogonale à
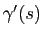 et indique la direction dans laquelle la courbe est courbée à l'ordre deux.
Nous introduisons maintenant plusieurs définitions
et indique la direction dans laquelle la courbe est courbée à l'ordre deux.
Nous introduisons maintenant plusieurs définitions
Définition 13
Soit
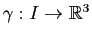 une courbe régulière paramétrée par abscisse curviligne de classe
une courbe régulière paramétrée par abscisse curviligne de classe 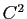 et
et 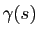 un point birégulier.
un point birégulier.
- Le plan osculateur en
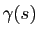 est le plan vectoriel engendré par
est le plan vectoriel engendré par
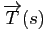 et
et
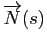
- Le rayon de courbure en
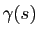 est
est
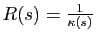 .
.
- Le centre de courbure en
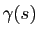 est
est
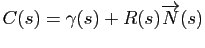 .
.
- La développée de
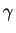 est l'ensemble des centres de courbure.
est l'ensemble des centres de courbure.
- La sphère osculatrice est la sphère de centre
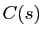 et de rayon
et de rayon 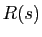 .
.
Remarque : Comme pour les courbes planes, on peut montrer que ces définitions ne dépendent pas de la paramétrisation de la courbe géométrique.
Binormale et repère de Serret-Frenet
Comme dans le cas des courbes planes, le repère de Serret-Frenet est un repère orthonormé qui varie le long d'une courbe paramétrée. Le vecteur
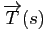 est unitaire tangent à la courbe, la normale principale
est unitaire tangent à la courbe, la normale principale
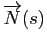 est orthogonale à
est orthogonale à
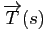 . Il est naturel de compléter cela en une base orthonormée en posant :
. Il est naturel de compléter cela en une base orthonormée en posant :
où 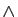 est le produit vectoriel défini par :
est le produit vectoriel défini par :
Définition 14
Soit
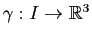 une courbe régulière paramétrée régulière et
une courbe régulière paramétrée régulière et 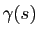 un point birégulier.
un point birégulier.
- La binormale à
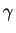 au point
au point 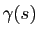 est le vecteur :
est le vecteur :
- Le repère de Serret-Frenet de
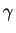 au point
au point 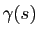 est le repère orthonormé direct :
est le repère orthonormé direct :
Torsion d'une courbe
On va maintenant étudier la torsion d'une courbe, autrement dit chercher à savoir comment "tourne" le repère de Serret-Frenet autour de la droite tangente à la courbe. Pour mesurer cela, on a besoin de la dérivée du vecteur binormal
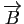 . Comme
. Comme
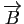 fait intervenir la dérivée seconde de la paramétrisation, on est obligé de considérer ici des paramétrisation de classe
fait intervenir la dérivée seconde de la paramétrisation, on est obligé de considérer ici des paramétrisation de classe 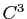 .
.
On considère ici une courbe
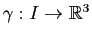 paramétrée normale de classe
paramétrée normale de classe 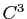 et
et 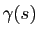 un point birégulier.
un point birégulier.
Proposition 9
Le vecteur
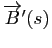 est colinéaire à
est colinéaire à
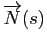 . En particulier, il existe une application continue
. En particulier, il existe une application continue
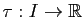 qui vérifie :
qui vérifie :
Démonstration : Pour tout 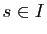 , on a
, on a
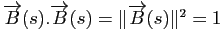 . En dérivant, on a:
. En dérivant, on a:
De même, en dérivant le fait que pour tout 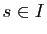
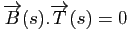 , on a :
, on a :
Le vecteur
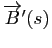 est donc orthogonal à
est donc orthogonal à
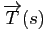 et
et
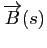 . Il est alors colinéaire à
. Il est alors colinéaire à
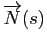 et on pose
et on pose
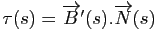 .
.
Définition 15
La torsion 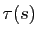 d'une courbe paramétrée par abscisse curviligne
d'une courbe paramétrée par abscisse curviligne 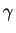 en un point
en un point 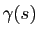 est :
est :
Proposition 10
La torsion est donnée pour tout 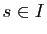 par :
par :
Démonstration : Cela consiste à faire le calcul suivant:
 En pratique, le résultat suivant peut permettre de calculer la torsion pour une paramétrisation générale.
En pratique, le résultat suivant peut permettre de calculer la torsion pour une paramétrisation générale.
Proposition 11
La torsion d'une courbe paramétrée
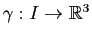 de classe
de classe 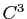 en un point
en un point 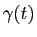 vaut
vaut
Démonstration : Admise.
La torsion mesure comment "tourne" le vecteur
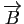 . Une interprétation géométrique de la torsion est donnée par la proposition suivante
. Une interprétation géométrique de la torsion est donnée par la proposition suivante
Proposition 12
Soit
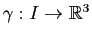 une courbe paramétrée régulière de classe
une courbe paramétrée régulière de classe 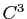 dont tous les points sont biréguliers. Alors
dont tous les points sont biréguliers. Alors
la courbe
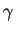
est plane
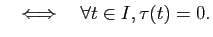
Démonstration : Voir exercice 15.
Formules de Serret-Frenet
Comme pour les courbes planes, en chaque point d'une courbe gauche paramétrée régulière, on a un repère de Serret Frenet. Ce repère bouge avec le paramètre de la courbe. Les formules de Serret-Frenet expriment justement la dérivée de ce repère.
Proposition 13 (Formules de Serret Frenet)
Soit
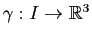 une courbe paramétrée normale régulière de classe
une courbe paramétrée normale régulière de classe 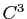 et
et 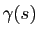 un point birégulier. Alors on a :
un point birégulier. Alors on a :
Démonstration : Il ne reste que la deuxième formule à montrer. Pour cela, on va calculer les coordonnées de
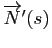 dans la base de Serret-Frenet.
dans la base de Serret-Frenet.
Pour tout 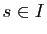 , on a
, on a
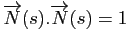 . En dérivant, cela donne :
. En dérivant, cela donne :
En dérivant le fait que pour tout 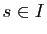
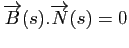 , on a :
, on a :
De même, en dérivant le fait que pour tout 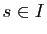
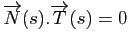 , on a :
, on a :

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
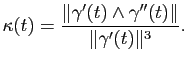
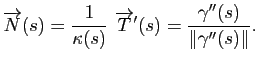
![]() est unitaire tangent à la courbe, la normale principale
est unitaire tangent à la courbe, la normale principale
![]() est orthogonale à
est orthogonale à
![]() . Il est naturel de compléter cela en une base orthonormée en posant :
. Il est naturel de compléter cela en une base orthonormée en posant :
![]() . Comme
. Comme
![]() fait intervenir la dérivée seconde de la paramétrisation, on est obligé de considérer ici des paramétrisation de classe
fait intervenir la dérivée seconde de la paramétrisation, on est obligé de considérer ici des paramétrisation de classe ![]() .
.
![]() paramétrée normale de classe
paramétrée normale de classe ![]() et
et ![]() un point birégulier.
un point birégulier.
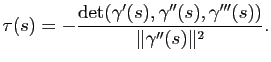
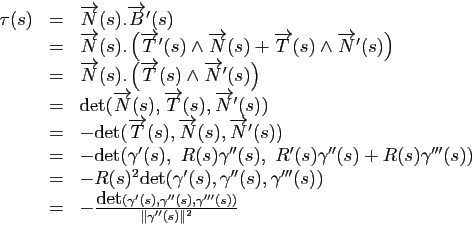
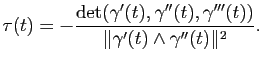
![]() . Une interprétation géométrique de la torsion est donnée par la proposition suivante
. Une interprétation géométrique de la torsion est donnée par la proposition suivante
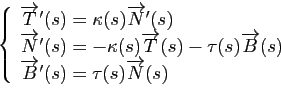
![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales