Dans cette partie, on va donner quelques rudiments concernant les surfaces paramétrées régulières. Comme dans le cas des courbes, la notion d'espace tangent est liée à la différentielle première et la forme de la surface est donnée par la différentielle seconde.
Définition des surfaces paramétrées
L'ensemble
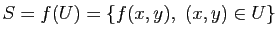 est appelé le support géométrique de la surface paramétrée
est appelé le support géométrique de la surface paramétrée
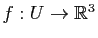 .
.
Figure 7:
Surface paramétrée
|
|
Reparamétrisation
Comme dans le cas des courbes, il est possible de reparamétrer les surfaces paramétrées par des difféomorphismes. Prenons une surface paramétrée
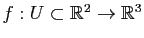 de classe
de classe 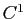 et
et
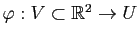 un
un 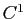 difféomorphisme. Alors
difféomorphisme. Alors
est une surface paramétrée qui a exactement le même support géométrique que 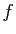 . On dit que
. On dit que 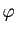 est un changement de variable admissible et que
est un changement de variable admissible et que
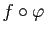 est une reparamétrisation de
est une reparamétrisation de 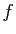 .
.
Rappel sur les différentielles
Le but de cette partie n'est pas de faire un cours précis sur les différentielles, mais de rappeler les notions utiles pour les surfaces. Pour plus de précisions, le lecteur pourra regarder le chapitre Fonctions de plusieurs variables de Maths en L gne. Prenons une application
gne. Prenons une application
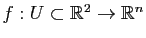 (avec
(avec 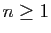 ).
).
On a alors la proposition suivante:
De même, on dit qu'une application
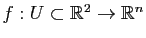 est de classe
est de classe 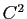 si les dérivées partielles d'ordre deux existent et sont continues. La différentielle seconde
si les dérivées partielles d'ordre deux existent et sont continues. La différentielle seconde
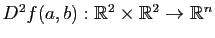 est alors une application bilinéaire donnée pour tout
est alors une application bilinéaire donnée pour tout
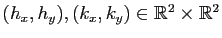 par :
par :
On a alors la proposition suivante :
Espace tangent à une surface
Prenons une surface paramétrée
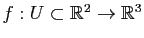 de classe
de classe 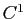 . Remarquons que si
. Remarquons que si
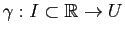 est une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres
est une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres 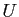 , alors l'application
, alors l'application
est une courbe paramétrée dont le support est inclus dans le support 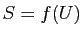 (Figure 8).
(Figure 8).
Figure 8:
Courbe sur une surface
|
|
En particulier, prenons un point
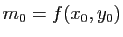 de la surface et considérons deux intervalles
de la surface et considérons deux intervalles 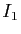 et
et 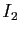 de
de
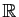 tels que
tels que
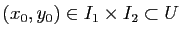 . On peut considérer la courbe coordonnée
. On peut considérer la courbe coordonnée
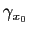 (avec
(avec
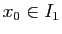 ) :
) :
Clairement,
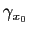 est une courbe paramétrée dont le support est inclus dans
est une courbe paramétrée dont le support est inclus dans 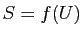 . Si cette courbe est régulière en
. Si cette courbe est régulière en 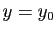 cela signifie que le vecteur
cela signifie que le vecteur
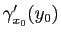 est tangent à la courbe
est tangent à la courbe
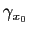 au point
au point
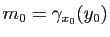 . De même, on peut considérer la courbe coordonnées
. De même, on peut considérer la courbe coordonnées
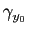 (avec
(avec
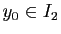 ) :
) :
Si cette courbe est régulière en 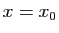 cela signifie que le vecteur
cela signifie que le vecteur
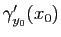 est tangent à la courbe
est tangent à la courbe
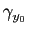 au point
au point
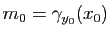 . Or, par définition des dérivées partielles, nous avons:
. Or, par définition des dérivées partielles, nous avons:
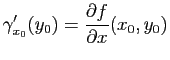
et
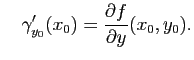
Figure 9:
Dérivées partielles de la paramétrisation
|
|
Ceci motive la définition d'espace tangent à une surface :
Définition 18
L'espace tangent à une surface paramétrée
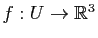 au point
au point
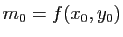 est l'espace affine, noté
est l'espace affine, noté 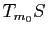 (avec
(avec 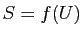 ) passant par
) passant par 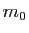 et engendré par les vecteurs
et engendré par les vecteurs
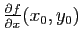 et
et
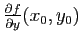 .
.
En pratique, l'espace tangent 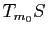 désigne aussi l'espace vectoriel qui dirige l'espace affine défini ci-dessus à savoir donc l'espace vectoriel engendré par les vecteurs
désigne aussi l'espace vectoriel qui dirige l'espace affine défini ci-dessus à savoir donc l'espace vectoriel engendré par les vecteurs
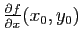 et
et
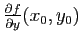 .
.
Définition 19
- La surface paramétrée
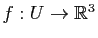 est dite régulière au point
est dite régulière au point 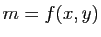 si les deux vecteurs
si les deux vecteurs
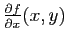 et
et
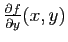 sont libres.
sont libres.
- La surface paramétrée
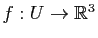 est dite régulière si elle est régulière en tout point.
est dite régulière si elle est régulière en tout point.
On peut montrer que cette définition ne dépend pas de la paramétrisation choisie. Au final, on peut retenir que si la surface est régulière, alors l'espace tangent 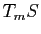 définit en tout point
définit en tout point 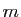 par l'application
par l'application 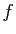 est de dimension deux : on l'appelle aussi plan tangent.
est de dimension deux : on l'appelle aussi plan tangent.
Figure 10:
Espace tangent d'une surface paramétrée régulière
|
|
Longueur et aire
Prenons une surface paramétrée
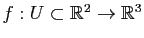 de classe
de classe 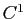 et
et
![$ \gamma: [a,b]\subset \mathbb{R}\to U$](img353.gif) une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres
une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres 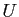 . Alors
. Alors
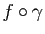 est une courbe paramétrée dont le support est inclus dans le support
est une courbe paramétrée dont le support est inclus dans le support 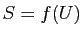 (Figure 8). Sa longueur est donnée par :
(Figure 8). Sa longueur est donnée par :
Autrement dit, pour connaître la longueur de la courbe
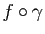 , on a besoin de la différentielle
, on a besoin de la différentielle 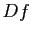 et de la dérivée de
et de la dérivée de 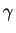 . Par ailleurs, on donne sans preuve le résultat qui donne l'aire d'une surface :
. Par ailleurs, on donne sans preuve le résultat qui donne l'aire d'une surface :
Proposition 16
Soit
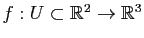 une surface paramétrée régulière de classe
une surface paramétrée régulière de classe 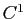 . Alors l'intégrale :
. Alors l'intégrale :
ne dépend pas de la paramétrisation.
Définition 20
L'aire de la surface 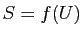 paramétrée par
paramétrée par
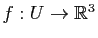 est :
est :
Exemple : On considère le tore de révolution
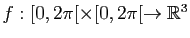 paramétré par :
paramétré par :
L'aire de cette surface est donnée par :
Allure locale d'une surface
On s'intéresse ici à la forme de la surface localement. Rappelons que pour les courbes paramétrées régulières, la dérivée de la paramétrisation donne un vecteur tangent à la courbe, et la dérivée seconde permet de calculer la courbure. Pour les surfaces, il en est de même : la différentielle de la paramétrisation 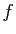 permet de définir l'espace tangent. Pour avoir une idée de la forme, on peut faire un développement limité à l'ordre deux.
permet de définir l'espace tangent. Pour avoir une idée de la forme, on peut faire un développement limité à l'ordre deux.
Cas particulier
Pour simplifier, on va supposer que la surface est paramétrée par une application de la forme :
avec
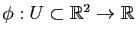 . (En fait, on peut montrer que l'on peut toujours se ramener localement à une telle forme, et que cette hypothèse n'est pas restrictive.) D'autre part, quitte à faire un changement de repère, on peut supposer que
. (En fait, on peut montrer que l'on peut toujours se ramener localement à une telle forme, et que cette hypothèse n'est pas restrictive.) D'autre part, quitte à faire un changement de repère, on peut supposer que
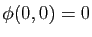 et que
et que
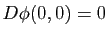 . Dans le nouveau repère, cela revient à avoir que la surface passe par le point de coordonnées
. Dans le nouveau repère, cela revient à avoir que la surface passe par le point de coordonnées 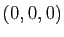 et que le plan tangent en ce point est horizontal. Dans ce cas là, le développement limité de
et que le plan tangent en ce point est horizontal. Dans ce cas là, le développement limité de 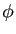 en
en 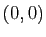 est :
est :
avec
La forme bilinéaire symétrique
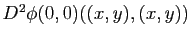 donne ainsi des informations sur l'allure de la surface au voisinage du point
donne ainsi des informations sur l'allure de la surface au voisinage du point
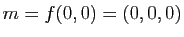 . Il s'agit de la deuxième forme fondamentale.
. Il s'agit de la deuxième forme fondamentale.
Cas général
Dans le cas d'une paramétrisation régulière quelconque, la définition de la deuxième forme fondamentale fait aussi intervenir la différentielle première. Rappelons que si
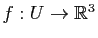 est une surface paramétrée régulière de classe
est une surface paramétrée régulière de classe 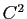 , alors les vecteurs
, alors les vecteurs
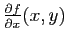 et
et
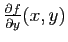 forment une base de l'espace tangent
forment une base de l'espace tangent 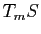 à
à 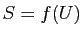 au point
au point 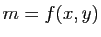 . Tout vecteur de
. Tout vecteur de 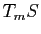 s'exprime donc dans cette base :
s'exprime donc dans cette base :
On note 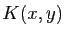 le vecteur orthogonal à l'espace tangent
le vecteur orthogonal à l'espace tangent 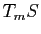 donné par :
donné par :
Définition 21
Soit
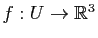 une surface paramétrée régulière de classe
une surface paramétrée régulière de classe 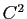 . La deuxième forme fondamentale
. La deuxième forme fondamentale 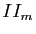 en un point
en un point 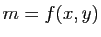 est la forme quadratique sur l'espace tangent
est la forme quadratique sur l'espace tangent 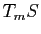 définie par :
définie par :
où
On peut montrer que la deuxième forme fondamentale 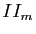 au point
au point 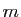 ne dépend pas (au signe près) du choix de la paramétrisation.
ne dépend pas (au signe près) du choix de la paramétrisation.
Remarques :
Comme 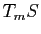 est un espace vectoriel de dimension deux munit d'un produit scalaire, on peut utiliser le résultat d'algèbre suivant :
est un espace vectoriel de dimension deux munit d'un produit scalaire, on peut utiliser le résultat d'algèbre suivant :
Proposition 17
Soient 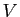 est un espace vectoriel de dimension deux munit d'un produit scalaire
et
est un espace vectoriel de dimension deux munit d'un produit scalaire
et
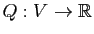 une forme quadratique sur
une forme quadratique sur 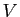 . Alors il existe une base orthonormée
. Alors il existe une base orthonormée 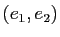 de
de 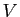 telle que :
telle que :
où
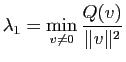
et
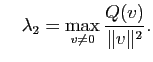
On peut montrer que si
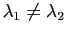 , alors la base orthogonale
, alors la base orthogonale 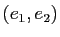 dans laquelle la forme quadratique est diagonale est unique (à l'orientation près des vecteurs).
En appliquant cette proposition à la deuxième forme fondamentale
dans laquelle la forme quadratique est diagonale est unique (à l'orientation près des vecteurs).
En appliquant cette proposition à la deuxième forme fondamentale 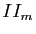 au point
au point 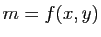 , on sait qu'il existe une base orthonormée
, on sait qu'il existe une base orthonormée 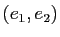 de
de 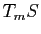 telle que :
telle que :
où
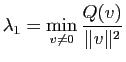
et
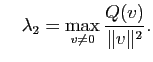
On définit alors :
Définition 22
- Les directions principales de
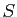 au point
au point 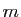 sont les vecteurs
sont les vecteurs 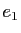 et
et 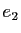 .
.
- Les courbures principales de
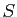 au point
au point 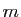 sont les nombres
sont les nombres 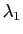 et
et 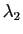 .
.
- La courbure de Gauss de
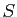 au point
au point 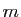 est le produit
est le produit
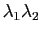 .
.
Interprétation géométrique
Pour tout vecteur
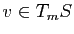 ,
, 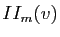 est la courbure de la surface au point
est la courbure de la surface au point 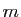 dans la direction
dans la direction 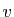 . En particulier,
. En particulier, 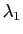 est la courbure de la surface
est la courbure de la surface 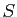 dans la direction
dans la direction 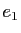 et
et 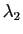 est la courbure de la surface
est la courbure de la surface 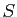 dans la direction
dans la direction 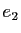 . Le résultat d'algèbre précédent est assez surprenant dans la mesure où il nous dit que pour tout point de toute surface régulière de classe
. Le résultat d'algèbre précédent est assez surprenant dans la mesure où il nous dit que pour tout point de toute surface régulière de classe 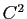 , la direction dans laquelle la surface est la plus courbée et la direction dans laquelle la surface est la moins courbée sont orthogonales.
, la direction dans laquelle la surface est la plus courbée et la direction dans laquelle la surface est la moins courbée sont orthogonales.
Figure 11:
Allure locale de la surface en fonction du signe des courbures principales
|
|
D'autre part, si on exprime localement la surface 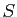 comme un graphe au-dessus de son espace tangent et que l'on met l'origine au point
comme un graphe au-dessus de son espace tangent et que l'on met l'origine au point 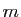 , on peut supposer que
, on peut supposer que
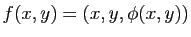 avec
avec
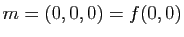 et
et 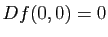 . De plus, si on exprime
. De plus, si on exprime 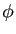 dans la base des directions principales
dans la base des directions principales 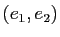 du plan tangent
du plan tangent 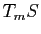 on a :
on a :
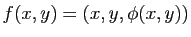
avec
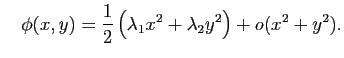
Il est clair sur cette formule que l'allure de la surface au voisinage du point 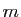 dépend du signe de
dépend du signe de 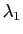 et de
et de 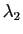 , (Figure 11):
, (Figure 11):
- Si
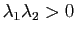 , la surface ressemble localement à un paraboloïde.
, la surface ressemble localement à un paraboloïde.
- Si
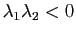 la surface ressemble localement à une "selle de cheval".
la surface ressemble localement à une "selle de cheval".
- Si
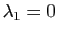 et
et
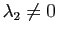 , la surface ressemble localement à un cylindrique.
, la surface ressemble localement à un cylindrique.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() de classe
de classe ![]() et
et
![]() un
un ![]() difféomorphisme. Alors
difféomorphisme. Alors
![]() gne. Prenons une application
gne. Prenons une application
![]() (avec
(avec ![]() ).
).
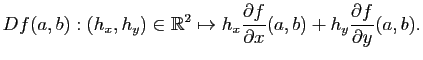
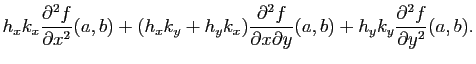
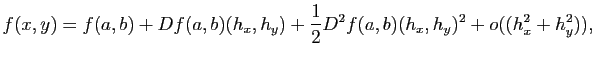
![]() de classe
de classe ![]() . Remarquons que si
. Remarquons que si
![]() est une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres
est une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres ![]() , alors l'application
, alors l'application
![]() de la surface et considérons deux intervalles
de la surface et considérons deux intervalles ![]() et
et ![]() de
de
![]() tels que
tels que
![]() . On peut considérer la courbe coordonnée
. On peut considérer la courbe coordonnée
![]() (avec
(avec
![]() ) :
) :
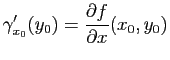 et
et 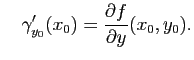
![]() de classe
de classe ![]() et
et
![]() une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres
une courbe paramétrée plane dont le support géométrique vit dans l'espace des paramètres ![]() . Alors
. Alors
![]() est une courbe paramétrée dont le support est inclus dans le support
est une courbe paramétrée dont le support est inclus dans le support ![]() (Figure 8). Sa longueur est donnée par :
(Figure 8). Sa longueur est donnée par :
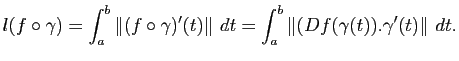
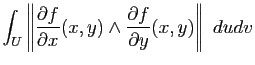
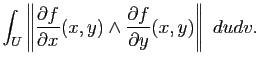
![]() paramétré par :
paramétré par :
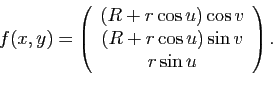
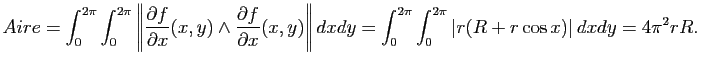
![]() permet de définir l'espace tangent. Pour avoir une idée de la forme, on peut faire un développement limité à l'ordre deux.
permet de définir l'espace tangent. Pour avoir une idée de la forme, on peut faire un développement limité à l'ordre deux.
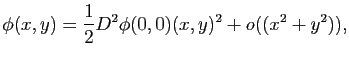
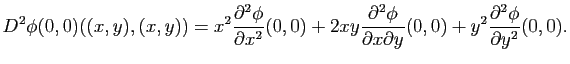
![]() est une surface paramétrée régulière de classe
est une surface paramétrée régulière de classe ![]() , alors les vecteurs
, alors les vecteurs
![]() et
et
![]() forment une base de l'espace tangent
forment une base de l'espace tangent ![]() à
à ![]() au point
au point ![]() . Tout vecteur de
. Tout vecteur de ![]() s'exprime donc dans cette base :
s'exprime donc dans cette base :
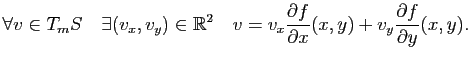
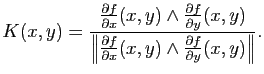
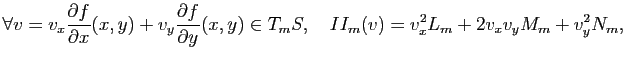
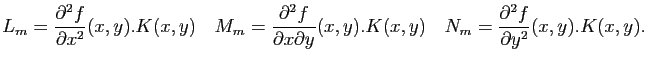
![]() est un espace vectoriel de dimension deux munit d'un produit scalaire, on peut utiliser le résultat d'algèbre suivant :
est un espace vectoriel de dimension deux munit d'un produit scalaire, on peut utiliser le résultat d'algèbre suivant :
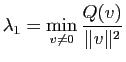 et
et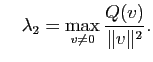
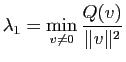 et
et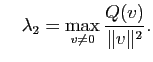
![]() ,
, ![]() est la courbure de la surface au point
est la courbure de la surface au point ![]() dans la direction
dans la direction ![]() . En particulier,
. En particulier, ![]() est la courbure de la surface
est la courbure de la surface ![]() dans la direction
dans la direction ![]() et
et ![]() est la courbure de la surface
est la courbure de la surface ![]() dans la direction
dans la direction ![]() . Le résultat d'algèbre précédent est assez surprenant dans la mesure où il nous dit que pour tout point de toute surface régulière de classe
. Le résultat d'algèbre précédent est assez surprenant dans la mesure où il nous dit que pour tout point de toute surface régulière de classe ![]() , la direction dans laquelle la surface est la plus courbée et la direction dans laquelle la surface est la moins courbée sont orthogonales.
, la direction dans laquelle la surface est la plus courbée et la direction dans laquelle la surface est la moins courbée sont orthogonales.
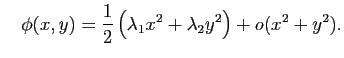
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales