Transformée en Cosinus Discrète par Bloc 8x8(DCT)

Rappels mathématiques

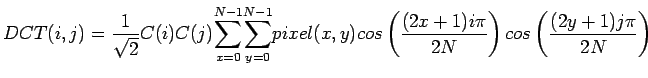
Le passage par la DCT a été l'idée majeure pour la compression JPEG. En effet ce processus appartient à une classe d'opérations mathématiques, tout comme la Transformée de Fourier. Elle permet un changement de domaine d'étude, tout en gardant exactement la même fonction étudiée. Dans notre cas, on étudie une image, c'est à dire une fonction à 3 dimensions : X et Y, indiquant le pixel, et Z avec la valeur du pixel en ce point. Dans le cas d'une image couleur, il faut donc considérer indépendamment 3 fonctions, pour chacun des canaux RGB.

L'application de la DCT, ou d'une Transformée de Fourier fait passer l'information de l'image du domaine spatial en une représentation identique dans le domaine fréquentiel. Pourquoi ce changement de domaine est-il si intéressant? Justement parce qu'une image classique admet une grande continuité entre les valeurs des pixels. Les hautes fréquences étant réservées à des changements rapides d'intensité du pixel, ceux-ci sont en général minimes dans une image. Ainsi on parvient à représenter l'intégralité de l'information de l'image sur très peu de coefficients, correspondant à des fréquences plutôt basses. La composante continue (valeur moyenne de l'image traitée) ayant une grande importance pour l'oeil.

La DCT s'applique à une matrice carrée. Le résultat fournit est représenté dans une matrice de même dimension. Les basses fréquences se trouvant en haut à gauche de la matrice, et les hautes fréquences en bas à droite.

La transformation matricielle DCT étant Orthogonale, elle s'accompagne d'une méthode d'inversion pour pouvoir revenir dans le domaine spatial. Ainsi après avoir fait des modifications dans le domaine fréquentiel, éliminer des variations de l'image quasiment invisibles par l'oeil humain, on retourne à une représentation sous forme de pixels.

Formule pour calculer la DCT sur une matrice NxN

$$DCT(i,j) = \frac{1}{\sqrt{2}}C(i)C(j)\displaystyle { \sum_{x=0}^{... ...x,y)cos\left(\frac{(2x+1)i\pi}{2N}\right)cos\left(\frac{(2y+1)j\pi}{2N}\right)$$

$C(x) = \frac{1}{\sqrt{2}}$ si x vaut 0, et 1 si x>0.

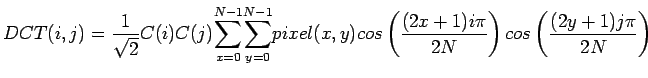
Formule pour calculer la IDCT sur une matrice NxN

$$pixel(x,y) = \frac{1}{\sqrt{2N}}\sum_{i=0}^{N-1} \sum_{j=0}^{N-1}... ...i,j)cos\left(\frac{(2x+1)i\pi}{2N}\right)cos\left(\frac{(2y+1)i\pi}{2N}\right)$$

$C(x) = \frac{1}{\sqrt{2}}$ si x vaut 0, et 1 si x>0.

Pourquoi la DCT?

On a vu que la DCT était dans la même classe d'outils mathématiques que la Transformée de Fourier. Alors pourquoi les membres du groupe JPEG ont-ils fait le choix de la DCT? Ces deux méthodes permettent une décomposition de l'information dans une autre base : Une base de cosinus, ou la base de Fourier. Cependant, La décomposition dans la base de Fourier soulève plusieurs problèmes : si l'image présente des discontinuités, alors la décroissance des coefficients de la transformée de Fourier n'est qu'en $\frac{1}{K}$, K étant l'indice du coefficient.

Figure: Decroissance des coefficients

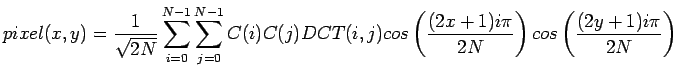
Dans cette figure, on se rend compte que pour restituer convenablement l'information, on a besoin de beaucoup plus de coefficients que pour une DCT. La décroissance des coefficients n'étant pas suffisante pour pouvoir négliger rapidement les coefficients de grands indices. De plus en tronquant les derniers coefficients, on risque de voir se produire à la fin le phénomène de Gibbs, qui se traduit par une oscillation au niveau des discontinuités.

D'autre part, la fonction doit être périodique pour la transformée de Fourier, sinon on se retrouve avec une discontinuité au bord. Là encore se posera le phénomène de Gibbs qui risque fort de dégrader l'image.

Le fait de décomposer la fonction sur une base de cosinus fait que la fonction sera symétrique par rapport à $-\frac{1}{2}$. Cependant la DCT pose un problème d'optimisation. En effet le calcul d'un coefficient nécessite $N^2$ multiplications, or il y a $N^2$ coefficients à calculer. Le coût d'une telle décomposition devient alors démeusuré si notre image est de taille 512x512. Ainsi, au lieu de traiter toute l'image, on découpe celle-ci en blocs 8x8. Ce choix représente un compromis performance qualité : en effet, en augmentant la taille de ces blocs, la compression serait meilleure, mais le coût en temps a été jugé trop grand. Sur chacun de ces blocs, on procède ensuite à une DCT.

Cela permet d'avoir un algorithme rapide. Cependant la DCT par blocs 8x8 est justement un des facteurs limitant de la compression JPEG : en effet lorsqu'on augmente la compression, on voit apparaitre ces blocs.

Algorithme de calcul pour la DCT

Une bonne manière d'implémenter la DCT par blocs serait de créer une matrice de la transformée de cosinus, C.

$$C_{i,j} = {\left[ \begin{array}{cc} \frac{1}{\sqrt{N}} &\ si... ...}{N}}cos( \frac{(2j+1)i\pi}{2N})&\ si\ i>0 \end{array}\right.}$$

Une fois cette matrice créée, on crée la matrice Ct qui correspond à la transposée de C. Ensuite la transformée par bloc 8x8 se réduit à deux multiplications matricielles :

$$DCT = C * Pixels * Ct$$

Donc le coût pour calculer la DCT sur un bloc se réduira à $2N$ multiplications sur des entiers, et $2N$ additions sur des entiers : cela représente un gain important par rapport à une simple double boucle sur les indices comme pourrait le laisser suggérer la formule initiale de la DCT. On passe d'un coût de O($N^2$) à un coût très intéressant de O($N$) pour calculer UN bloc.