| Introduction |
| Configuration |
| Framework |
| Tutorial and tests |
| Download |
| An example
case 2 |
We want to simulate a dynamical system with only one state on nodes called mX and one state on edge called mY
The equations of the state on the node i is:
dmX/dt=6/n where n is the number of connection of node i.
The Fi function code is:
double fi=0;
vector<double> xjs=xj.find("mX")->second;
int n=xjs.size();
if (n>0) fi=6/n;
return fi;
The state eqution of edge is given by the equation: dmY/dt=1
The Gij function code is:
double gij=1;
return
gij;
double y_ij=yij.find("mY")->second;
bool isVerified=false;
if (y_ij>=5) {
isVerified=true;
} else {
double der=der_yij.find("mY")->second;
if (der!=0) dt=(5-y_ij)/der;
}
return isVerified;
the reset edge function is as follow:

The secund constraint is an edge splitting: the edge [i,j] verified its
test function then a node k is created and also 2 edges between node i
and k and node j and k.
The test function is as following:
double x_i=xi.find("mX")->second;
double x_j=xj.find("mX")->second;
double xprime_i=der_xi.find("mX")->second;
double xprime_j=der_xj.find("mX")->second;
bool isVerified=false;
if ((x_i+x_j) >=12) {
isVerified=true;
} else {
double der=(xprime_i+xprime_j);
if (der!=0) dt=(12-x_i-x_j)/(xprime_i+xprime_j);
}
return isVerified;
The state of the added edges are set to 0.
yil=0;
yjl=0;
The state of all nodes are set to 0.
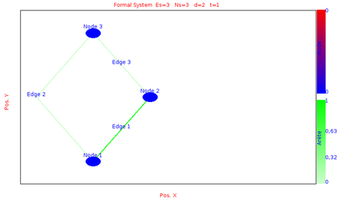
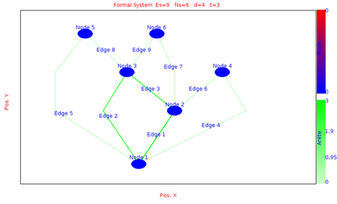
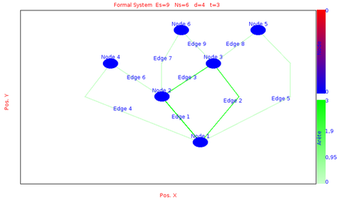
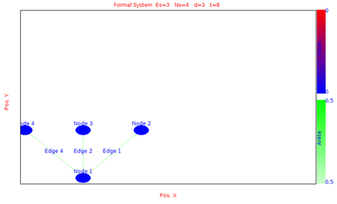
So the global state initialisation is activated and at each graph transformation the node are set to 0.We simulate the evolution of the system between time 0 and time 15 with max time step sets to 1 and min time step sets to 0.1
We obtains the following results at different time by choosing the layout equals to Hierarchical Layout:
 |
 |
 |
 |
 |
 |
 |
 |
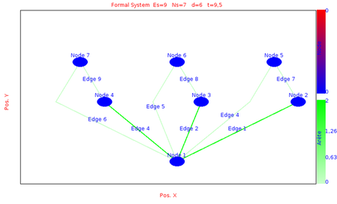 |
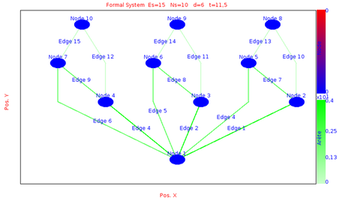 |
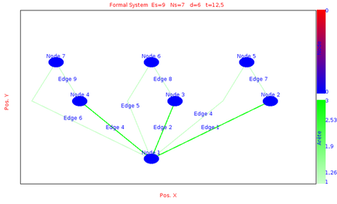 |
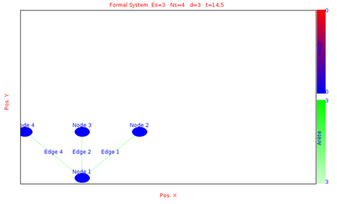 |
