| Introduction |
| Configuration |
| Framework |
| Tutorial and tests |
| Download |
| An example
case 1 |
We want to simulate a dynamical system with only one state on nodes call mX.
The equations of the state on the node i is:
dmX/dt=2-n/2 where n is the number of connection of node i.
The Fi function code is:
int n=xj.find("mX")->second.size();
double fi=2-(((double)n)/2);
cout << "fi:"<<fi<<"\n";
return fi;
There is only one constraint which is adding a node j to the node i if the state value of node i is greater than 10.
If the constraint is not
verified, a maximum time step is computed to forseen when the next constraint at the node i will appear.
The test function of the constraint is:
bool v=false;
double x_value=xi.find("mX")->second;
if (x_value>=10) {
v=true;
cout << "constraint verified ! \n";
} else {
int n=xj.find("mX")->second.size();
double fi=2-(((double)n)/2);
double dx=10-x_value;
if (fi>0) dt=dx/fi;
cout << "constraint unverified !\n";
}
return v;
When the constraint is verified, a local reset node function has to be defined. In that case, we set the i state node to 8 and the new node has its state initialized to 2. We set this code to the node reset function of the constraint:
xi=8;
xj=2;
In this case, we do not want to initialize all the state to a predefined value. So the global state initialisation is not activated.
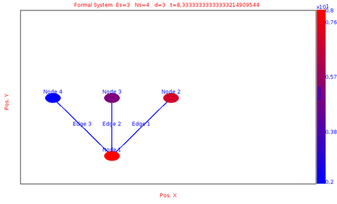
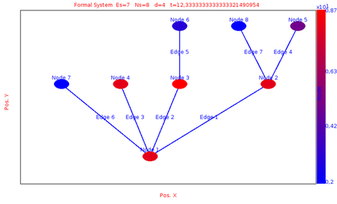
We simulate the evolution of the system between time 0 and time 13 with max time step sets to 1 and min time step sets to 0.1
We obtain the following results at different time by choosing the layout equals to Hierarchical Layout:
 |
 |
 |
 |
 |
 |
