• HOME
• RESEARCH
• COMMUNICATIONS
• TEACHING

• RESOURCES

  SHAPE OPTIMIZATION    SOFTWARES

• LINKS

The Mmg project gathers tools for improving two- and three-dimensional meshes; the main contributors to the project are (C.D.), Cécile Dobrzynski, Pascal Frey and Algiane Froehly. See the webpage of the project, or follow the GitHub link to get started using Mmg!

mmg3d (version 5)

Discrete domain remeshing

mmg3d is a tetrahedral mesh modification tool developped by Cécile Dobrzynski and Pascal Frey, taking as an input a tetrahedral mesh {\mathcal T} , and modifying it into a well-shaped triangulation, with respect to an input metric tensor field when such is supplied. Till version 4, mmg3d has been working in both isotropic and anisotropic contexts, but did not allow to remesh the surface part of {\mathcal T} . This new version does not yet allow for anistropic remeshing, but allows to remesh at the same time the volumic part of {\mathcal T} and its surfacic part (or any surface discretized in {\mathcal T} ).

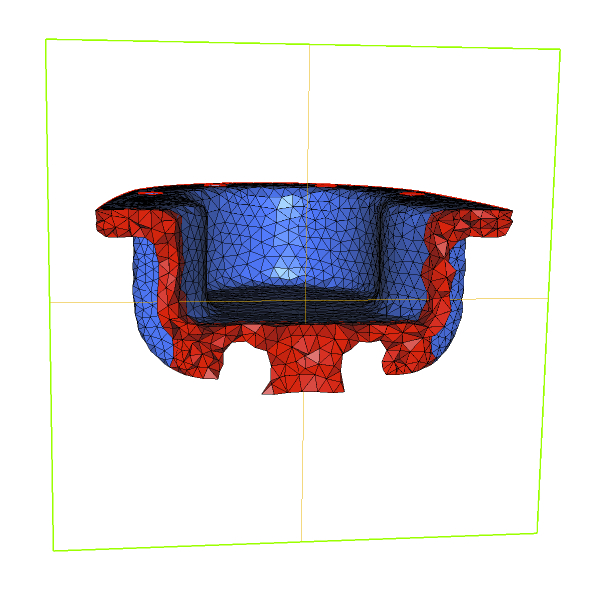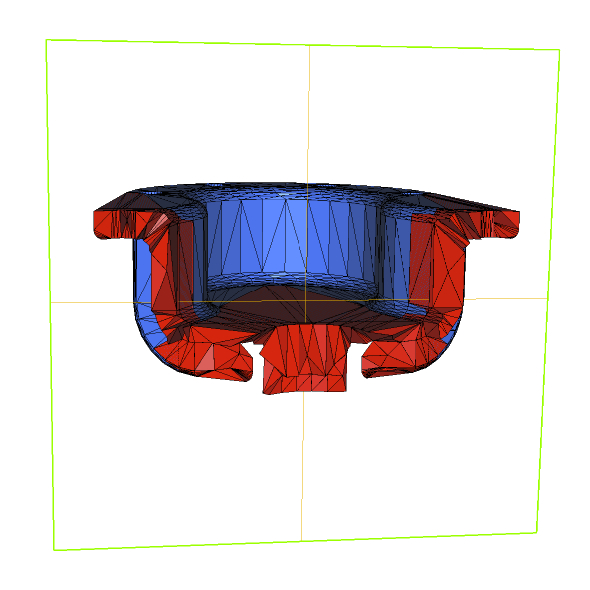
Remeshing of a ill-shaped mesh of a mechanical part (left : initial mesh and cut ; right : final result and corresponding cut)

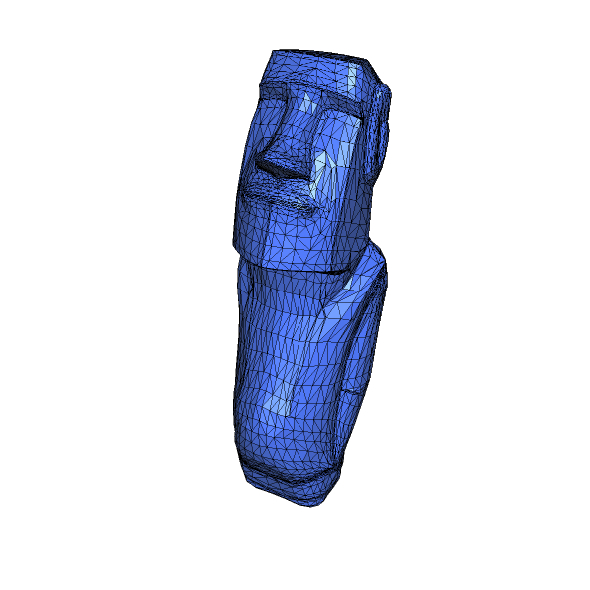
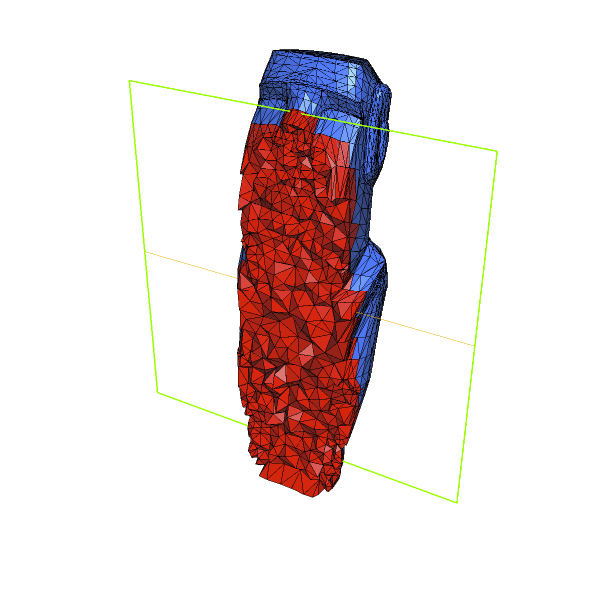
Remeshing of a ill-shaped mesh of a statue (left : initial mesh and cut ; right : final result and corresponding cut)

mmgs

Discrete surface remeshing

mmgs is a tool for remeshing an arbitrary surface triangulation into a well-shaped, well-sampled surface mesh, closely approximating a guessed underlying continuous surface to the intial datum. This code uses ony local mesh operators (splits, collapses, swaps,...), and works for now in the context of isotropic surface remeshing. An extension to anisotropic surface remeshing is ongoing.

Remeshing of ill-shaped meshes (left : initial triangulations ; right : final result)

This code takes as an input a computational triangular mesh {\mathcal T} , a velocity field V defined as a \mathbb{P}^1 function, a scalar \mathbb{P}^1 function \phi^0 over {\mathcal T} , and computes the solution of the transport equation of \phi^0 along V , for an arbitrary period of time, using the method of characteristics. This can be used for approximating the level set evolution equation.

You may download and install advect from the associated the GitHub link.

This code, written with Pascal Frey, takes as an input a computational triangular mesh {\mathcal T} (e.g. a big box), and a discrete contour (a curve given as list of segments in 2d, or a surface mesh in 3d), and approximates the signed distance function to this contour at the nodes of {\mathcal T} . This can be used in the context of the level set method, when initializing the level set function (a mode of the code includes the very similar redistancing procedure).

You may download and install mshdist from the associated the GitHub link.