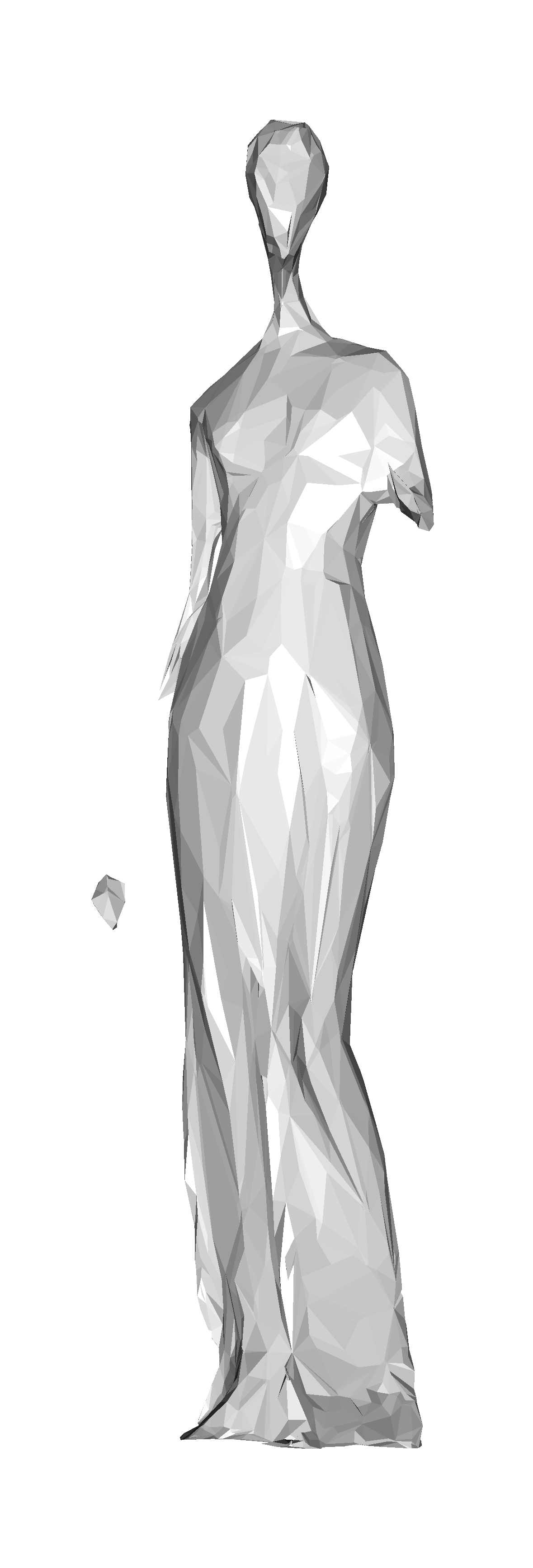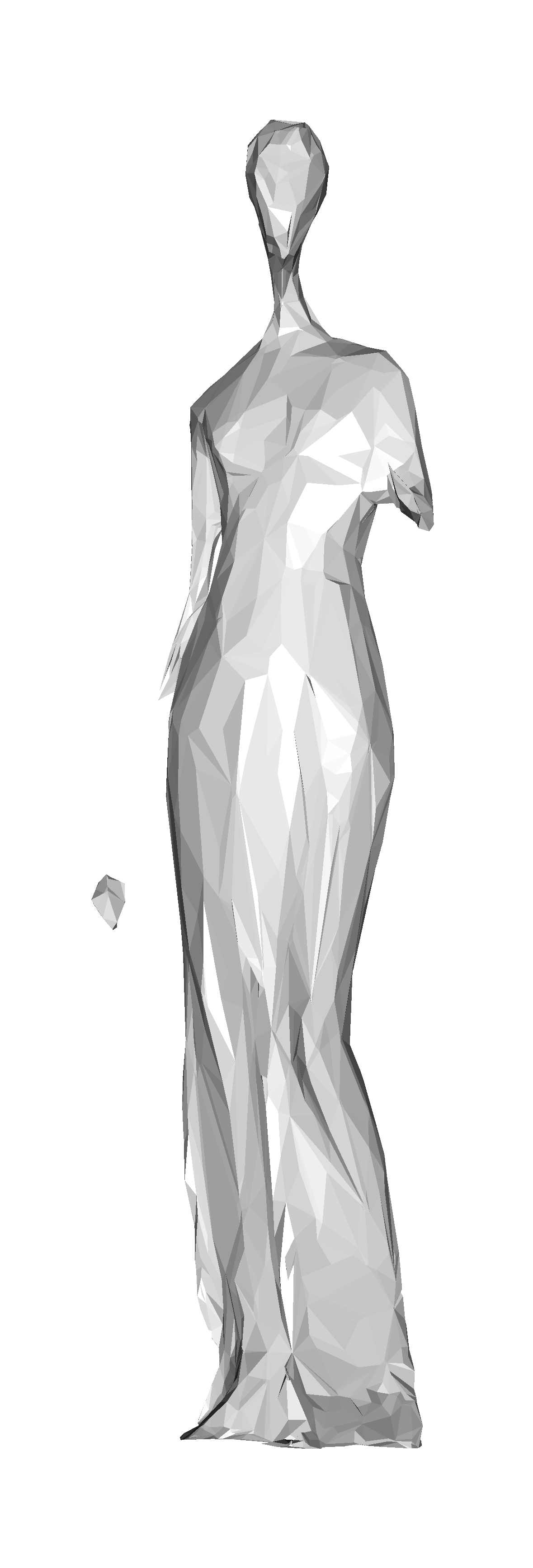• HOME
• RESEARCH
• COMMUNICATIONS
• TEACHING

• RESOURCES

  SHAPE OPTIMIZATION    SOFTWARES

• LINKS

Let \Omega \subset \mathbb{R}^d a bounded domain, {\mathcal S} a surface triangulation of \partial \Omega. Let D a large computational box, endowed with a simplicial mesh {\mathcal T}. A level set function associated to \Omega is often generated as the signed distance function d_\Omega to \Omega, for its unit gradient property
\lvert \lvert \nabla d_\Omega(x) \lvert \lvert = 1 \mbox{ a.e } x \in \mathbb{R}^d, which is of tremendous importance in numerical applications. Pascal Frey and I developed an algorithm for generating a piecewise linear approximation of d_\Omega on {\mathcal T}, which first creates any (possibly very irregular) level set function \phi_0 associated to \Omega, then solves the unsteady Eikonal equation :
\left\{ \begin{array}{ccc} \frac{\partial \phi}{\partial t} + \mbox{sgn}(\phi_0)\left(\lvert\lvert \nabla \phi \lvert\lvert -1 \right) = 0 & \mbox{for} & (t,x) \in (0,\infty)\times \mathbb{R}^d\\ \phi(0,.) = \phi_0 &\mbox{for}& x \in \mathbb{R}^d \end{array} \right. , relying on a numerical scheme based on some theoretical properties of this equation.
In a second time, we devised a process to adapt the computational mesh {\mathcal T} into a new mesh \widetilde{\mathcal T} which is amenable for an accurate computation of d_\Omega, and at the same time an accurate reconstruction of \partial \Omega as the 0 isosurface of the computed approximation to d_\Omega (up to a user-defined tolerance).

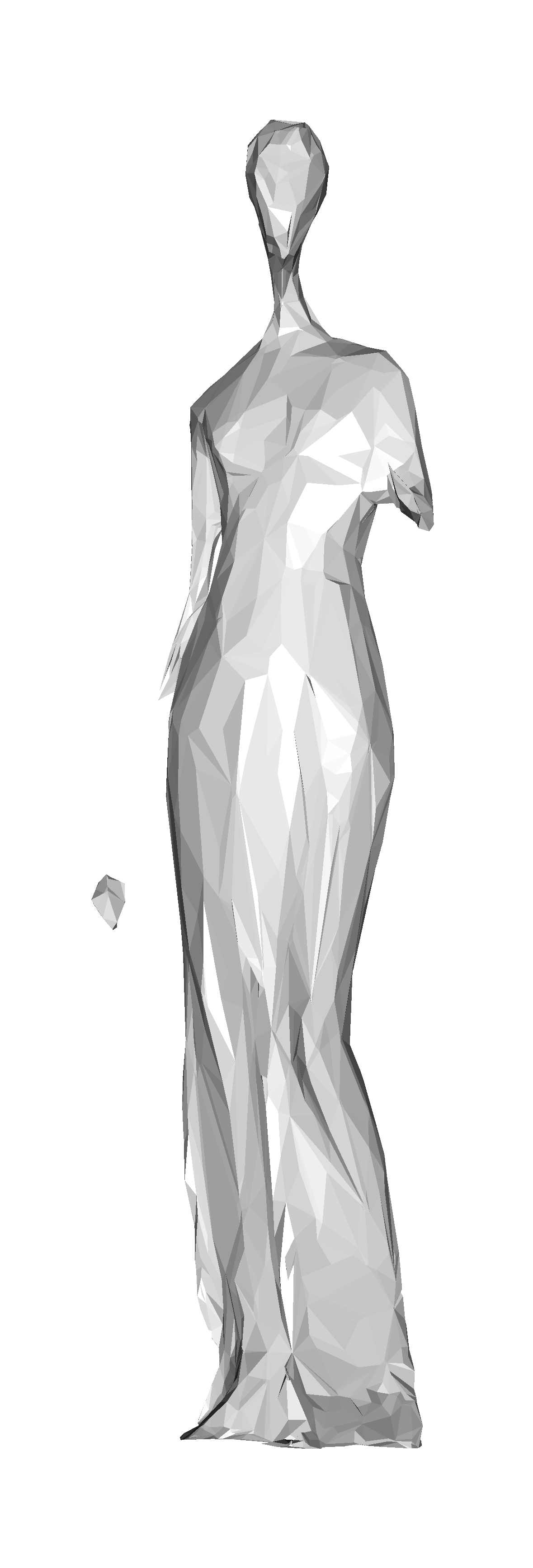Isosurfaces of the signed distance function to the Venus' (left), computed on an anisotropic adapted background mesh

Let \Omega(t) \subset \mathbb{R}^d an evolving domain along a velocity field V(t,x). The motion of \Omega(t) is translated in terms of an associated level set function \phi(t,.) as the so-called level set advection equation :
\left\{ \begin{array}{ccc} \frac{\partial \phi}{\partial t}(t,x) + V(t,x).\nabla \phi(t,x) = 0 & \mbox{for} & (t,x) \in (0,T) \times \mathbb{R}^d\\ \phi(0,.) &\mbox{given on}&\mathbb{R}^d \end{array} \right. . From the method of characteristics, Cuc Bui, Pascal Frey and I devised a simple numerical scheme to solve this equation on a simplicial mesh, in two and three space dimensions. As this scheme is low-order and dissipative, we also devised a mesh adaptation process to enhance its accuracy.

Cut on a three-dimensional mesh adapted with respect to both 0 level sets at two consecutive time steps

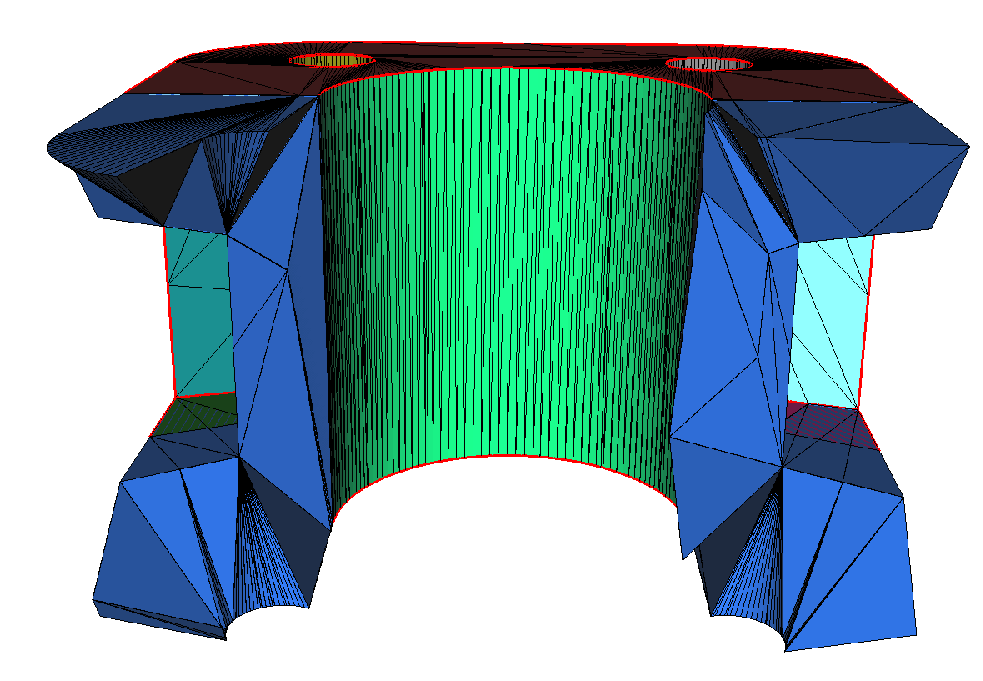
Cécile Dobzrynski, Pascal Frey and I developed local remeshing algorithms with the final aim to mesh the negative subdomain of a level set function supported on a computational mesh.

As a first step, we were led to investigate on surface remeshing : an initial surface triangulation {\mathcal T} of a continuous ideal surface {\mathcal S} is supplied, which is possibly ill-shaped, oversampled or undersampled. A local surface model is computed first, so as to infer a piece of {\mathcal S} from a local configuration on {\mathcal T}. Then, using carefully-driven local remeshing operators, such as edge splits, edge collapses, a new, well-shaped triangulation \widetilde{\mathcal T} of {\mathcal S} is obtained.

These ideas were next coupled with a subsequent short mathematical analysis to provide a model for anisotropic surface remeshing.

We then extended this strategy to deal with full 3d remeshing: from an initial tetrahedral mesh of a continuous ideal domain \Omega \subset \mathbb{R}^3, of possibly poor mesh quality, a new well-shaped mesh is computed, which is a close geometric approximation of \Omega. As a special case, and with rather few adaptations of the procedure, the 0 level set of some scalar function \phi defined at the vertices of the original mesh {\mathcal T} can be meshed, by first discretizing it explicitly into {\mathcal T} using a simple pattern-based procedure, then remeshing the resulting ill-shaped mesh into a fine one.

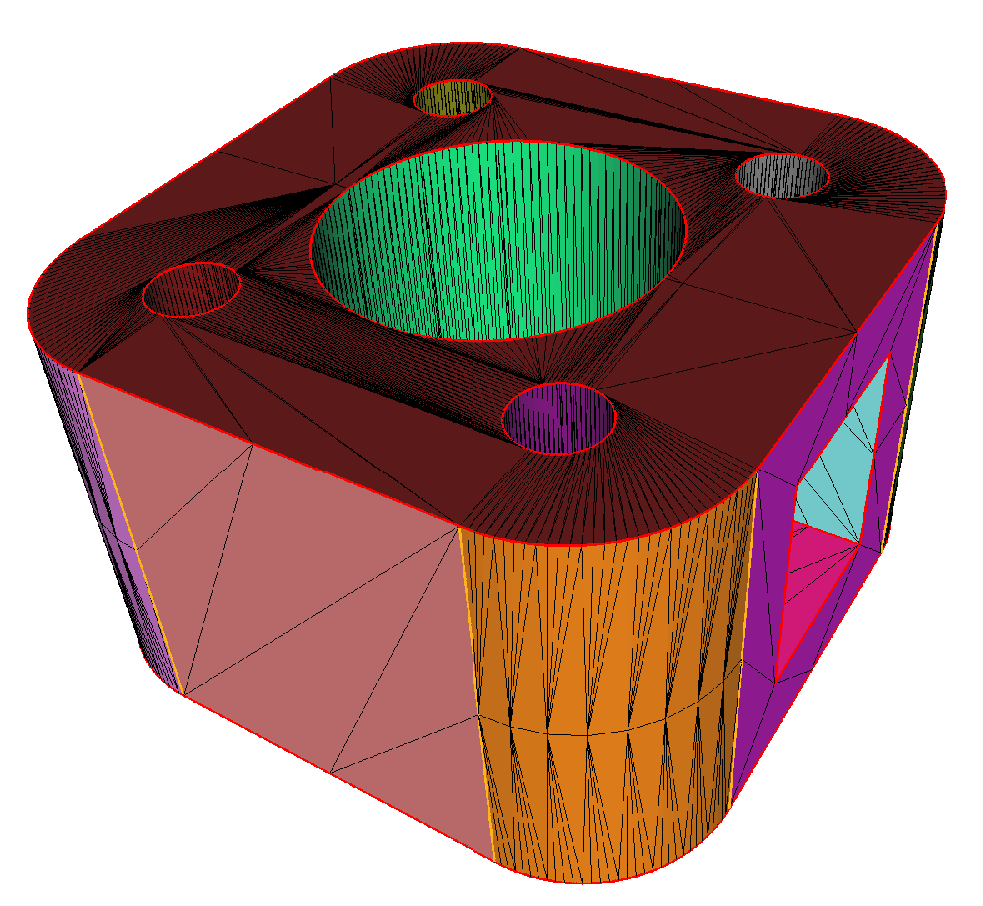Remeshing of a Three-dimensional model model. (tpp) Initial mesh {\mathcal T}; (bottom) final result \widetilde{\mathcal T}.

(Left) : Isosurfaces of the implicit function u on the initial mesh {\mathcal T}, (middle) result of the computation (only the surface mesh is represented), (right) a cut in the final mesh \widetilde{\mathcal T}.

A shape optimization problem generally presents as follows : from an initial shape \Omega^0, one aims at minimizing an objective functional J(\Omega) which depends on the domain, over a set {\mathcal U}_{ad} of admissible shapes.
As an example, the considered shapes may be filled with a linear elastic material of Hooke's law A, and the functional at play may be the work of external loads exerted on \Omega :
J(\Omega) = \int_\Omega{Ae(u_\Omega) : e(u_\Omega) \: dx}, where u_\Omega is the solution to the linear elasticity system on \Omega. In this context, {\mathcal U}_{ad} typically accounts for a volume constraint, etc...
One way to parametrize such problems is Hadamard's boundary variation method : the considered variations of a Lipschitz domain \Omega are of the form (I+\theta)(\Omega), for small vector fields \theta \in W^{1,\infty}(\mathbb{R}^d,\mathbb{R}^d). This allows for a notion of derivation with respect to the domain, then for the development of so-called shape gradient iterative algorithms for minimizing J over {\mathcal U}_{ad}.

However, in the sought applications, evaluating J, and computing an associated descent direction at each stage \Omega^n of the algorithm requires to solve PDE problems on the corresponding domain, which is typically carried out using the finite elements method on a mesh of \Omega^n. Hence the need to account for the evolution of a mesh of the different considered shapes.

To address this thorny problem, G. Allaire, F. Jouve and A.-M. Toader advocated the use of a level set method : all the considered shapes \Omega^n are embedded in a large computational domain D, meshed once and for all (e.g. with a cartesian mesh, which enables the use of finite difference numerical methods), and are considered via an associated level set function \phi^n. The so-called Ersatz material approach is used to transfer the exact PDE problems on \Omega^n to the whole domain D, under approximate form.

Grégoire Allaire, Pascal Frey and I proposed to elaborate on this process to devise a geometric shape optimization method : the computational domain D is equipped with a simplicial mesh {\mathcal T}^n, which is modified at each iteration, so that the 0 level set of \phi^n is explicitly discretized into it. Doing so, \Omega^n is explicitly meshed at each iteration, as a submesh of {\mathcal T}^n.

Some illustrations of this shape optimization process are reported herebelow. Click on the pictures to display the animation corresponding to the associated minimizing sequences of shapes.

Shape optimization of a bridge
Shape optimization of an electric mast	Shape optimization of a L-Beam with respect to a stress-based criterion
Optimal distribution of two materials within a beam

  As a joint work with Grégoire Allaire, Gabriel Delgado and Georgios Michailidis, we got interested in the shape-sensitivity analysis of the signed distance function d_\Omega to a domain \Omega \subset \mathbb{R}^d, and of some related pointwise or integral quantities. For instance, if D is a large (bounded) computational domain, which encloses all the shapes under consideration, and j : \mathbb{R} \rightarrow \mathbb{R} is a function of class {\mathcal C}^1, we proved that the functional J(\Omega) defined as:
J(\Omega) = \int_D{j\left( d_\Omega(x)\right)dx}, is shape differentiable, and if \Omega is assumed smooth enough, its shape derivative can be put under the following convenient form:
\forall \theta \in W^{1,\infty}(\mathbb{R}^d,\mathbb{R}^d), \:\: J^\prime(\Omega)(\theta) = -\int_{\partial \Omega}{j\prime(y)\left( \int_{p_{\partial \Omega}^{-1}(y) \cap D}{ \prod_{i=1}^{d-1}{\left(1 + d_\Omega(s)\kappa_i(y)\right)}ds}\right)\theta(y).n(y)dy}, where the \kappa_i are the principal curvature of \partial \Omega, and p_{\partial \Omega} : \mathbb{R}^d \rightarrow \partial \Omega is the projection application.

  This finds an interesting application in a numerical method for finding the optimal distribution (\Omega^0,\Omega^1) of two (or more) elastic materials with different Hooke's tensors A_0,A_1 within a fixed computational domain D. If \chi denotes the characteristic function \Omega^0, and A_\chi := A_0 + (1-\chi)(A_1-A_0) stands for the total Hooke's tensor, one aims at optimizing a functional of \Omega^0 such as the resulting compliance:
J(\Omega^0) = \int_D{A_\chi e(u_\chi):e(u_\chi) dx}, where u_\chi is the solution to the linearized elasticity system over D with Hooke's tensor A_\chi. A closely-related problem - which can either be understood as a numerical approximation of the previous one, or as a problem of independent relevance - arises when the discontinuous tensor A_\chi is smeared over a uniform width \varepsilon around \partial \Omega^0, i.e. A_\chi is replaced by A_\varepsilon := A_0 +h_\varepsilon(d_{\Omega^0})(A_1-A_0), where h_\varepsilon is a smooth approximation to the Heaviside function.
  We devised a level set method adapted to the numerical resolution of the latter problem, and analyzed its theoretical connections with the former one. An example of optimization of the distribution between three different materials is reported in the figure below.

Initial distribution of materials within a computational domain D.	Optimal distribution of the three materials and void within D.