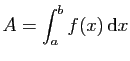 . On écrit aussi :
. On écrit aussi :
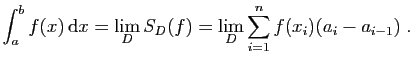
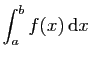 est la limite
des sommes de Riemann, lorsque la subdivision
est la limite
des sommes de Riemann, lorsque la subdivision
![$\displaystyle \Big(\forall x\in[a,b] ,\;f(x)=k\Big)\;\Longrightarrow\;
S_D(f)= k(b-a)\;.
$](img71.gif)
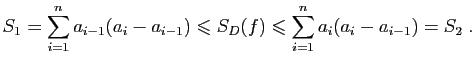
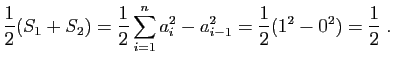
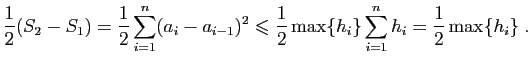
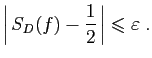
Considérons par exemple la somme :
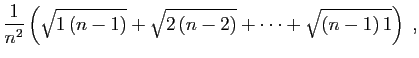
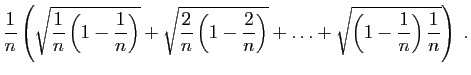
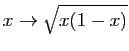 sur l'intervalle
sur l'intervalle 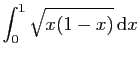 .
Or, le graphe de cette fonction est un demi-cercle de rayon
.
Or, le graphe de cette fonction est un demi-cercle de rayon
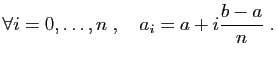
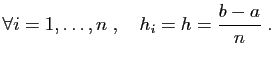
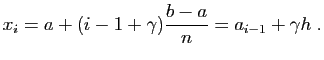
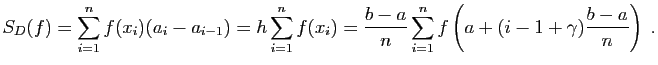
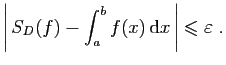
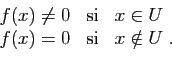
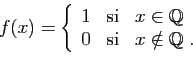
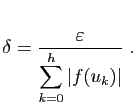
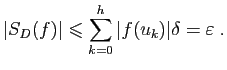
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales