Le principal problème des suites récurrentes est que
selon la valeur initiale 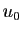 et la fonction
et la fonction 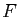 que l'on itère, tous les
comportements sont possibles, même les plus sauvages. Pour vous
en convaincre, essayez de suivre le plus longtemps possible la toile
d'araignée de la figure 5.
que l'on itère, tous les
comportements sont possibles, même les plus sauvages. Pour vous
en convaincre, essayez de suivre le plus longtemps possible la toile
d'araignée de la figure 5.
Figure 5:
Comportement chaotique d'une suite récurrente.
|
|
Il existe pourtant une situation particulièrement agréable, celle
où l'application 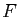 est contractante.
est contractante.
Théorème 12
Soit 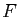 une application contractante. Alors
une application contractante. Alors 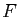 possède un point
fixe unique et pour tout
possède un point
fixe unique et pour tout 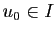 la suite des itérés
la suite des itérés
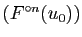 converge vers ce point fixe.
converge vers ce point fixe.
La démonstration sera l'occasion d'utiliser
la notion de suite de Cauchy.
Démonstration : Notons
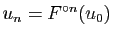 . Nous allons montrer que la suite
. Nous allons montrer que la suite
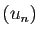 est une suite de Cauchy.
Observons que pour tout
est une suite de Cauchy.
Observons que pour tout
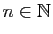 ,
,
et donc par récurrence,
Utilisons l'inégalité
triangulaire pour écrire :
Comme 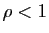 , la suite géométrique
, la suite géométrique 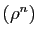 tend vers 0,
donc la distance
tend vers 0,
donc la distance
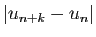 peut être rendue arbitrairement
petite, pour
peut être rendue arbitrairement
petite, pour 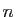 assez grand. Donc
assez grand. Donc 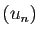 est une suite de Cauchy.
est une suite de Cauchy.
Par le théorème 8, la suite 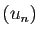 converge. Soit
converge. Soit
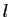 sa limite. La suite
sa limite. La suite 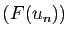 est
telle que :
est
telle que :
Donc 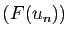 converge vers
converge vers 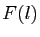 (
(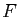 est continue) et
est continue) et 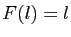 .
S'il y avait deux points fixes différents
.
S'il y avait deux points fixes différents 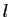 et
et 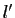 , ils seraient
tels que
, ils seraient
tels que
ce qui est impossible.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et la fonction
et la fonction ![]() que l'on itère, tous les
comportements sont possibles, même les plus sauvages. Pour vous
en convaincre, essayez de suivre le plus longtemps possible la toile
d'araignée de la figure 5.
que l'on itère, tous les
comportements sont possibles, même les plus sauvages. Pour vous
en convaincre, essayez de suivre le plus longtemps possible la toile
d'araignée de la figure 5.
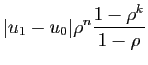
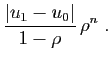
![]() converge. Soit
converge. Soit
![]() sa limite. La suite
sa limite. La suite ![]() est
telle que :
est
telle que :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales