Supposons que l'on souhaite résoudre numériquement l'équation
La méthode consiste à écrire une solution 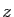 comme point fixe
d'une fonction
comme point fixe
d'une fonction 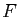 , choisie de manière à être contractante, avec
le meilleur rapport de contraction possible sur un intervalle
contenant
le point fixe.
Supposons que
, choisie de manière à être contractante, avec
le meilleur rapport de contraction possible sur un intervalle
contenant
le point fixe.
Supposons que 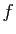 soit une application
dérivable de
soit une application
dérivable de
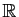 dans
dans
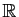 , et
que l'on connaisse une valeur
, et
que l'on connaisse une valeur
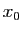 pas trop éloignée de la solution. L'équation de la
tangente en
pas trop éloignée de la solution. L'équation de la
tangente en 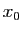 au graphe de
au graphe de 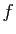 est :
est :
Si
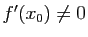 ,
cette droite coupe l'axe des
,
cette droite coupe l'axe des 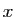 au point :
au point :
Il est raisonnable d'espérer que 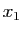 soit beaucoup plus proche de la
solution cherchée que
soit beaucoup plus proche de la
solution cherchée que 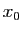 . La suite itérative que l'on se propose de
calculer est donc
. La suite itérative que l'on se propose de
calculer est donc
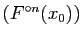 , avec :
, avec :
(Il faut bien sûr s'assurer que la suite est bien définie,
c'est-à-dire que pour tout 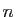 ,
,
 .)
.)
Par exemple, si on souhaite calculer numériquement 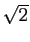 , on
pourra l'écrire comme solution de l'équation
, on
pourra l'écrire comme solution de l'équation 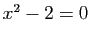 , et
contruire la suite définie par
, et
contruire la suite définie par 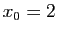 et
pour tout
et
pour tout
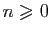 :
:
La figure 6 montre une illustration
graphique.
Figure 6:
Méthode de Newton.
|
|
La précision de la méthode est décrite
par le théorème suivant, que nous admettrons.
La majoration (2) traduit une convergence extrêmement
rapide. Supposons pour fixer les idées que 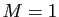 et
et
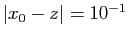 ,
alors la précision sera de
,
alors la précision sera de 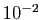 à la première itération,
à la première itération,
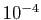 à la seconde,
à la seconde, 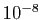 à la troisième, et on peut
s'attendre à
à la troisième, et on peut
s'attendre à 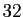 décimales exactes à la cinquième itération.
Chaque itération double le nombre de décimales exactes. En ce qui
concerne la constante
décimales exactes à la cinquième itération.
Chaque itération double le nombre de décimales exactes. En ce qui
concerne la constante 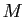 , il est intuitivement normal que la
méthode soit d'autant plus performante
que la dérivée seconde est plus faible
(la courbe est plus proche de sa tangente), et la dérivée plus grande.
, il est intuitivement normal que la
méthode soit d'autant plus performante
que la dérivée seconde est plus faible
(la courbe est plus proche de sa tangente), et la dérivée plus grande.
Exemple : Reprenons l'équation 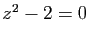 , en partant de
, en partant de
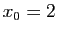 .
Voici les
.
Voici les 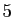 premières valeurs de la suite
premières valeurs de la suite
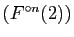 , à comparer
avec
, à comparer
avec
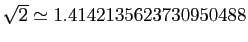 .
.
La méthode de Newton est extrêmement précise.
En revanche, elle nécessite une initialisation
relativement proche de la solution que l'on
cherche. Utiliser la méthode à partir d'un point quelconque
peut conduire à des résultats numériquement instables,
dans la mesure où deux suites récurrentes, même si elles partent
de points très voisins, peuvent converger vers des valeurs très
éloignées.
Exemple : Considérons l'équation
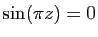 , dont les solutions
sont les entiers relatifs. Si
, dont les solutions
sont les entiers relatifs. Si
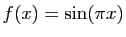 , alors :
, alors :
Le tableau ci-dessous donne les valeurs de
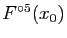 pour quelques valeurs
de
pour quelques valeurs
de 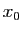 proches de
proches de 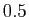 , valeur en laquelle
, valeur en laquelle 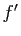 s'annule.
s'annule.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
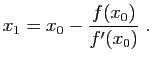
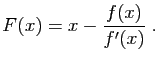
![]() , on
pourra l'écrire comme solution de l'équation
, on
pourra l'écrire comme solution de l'équation ![]() , et
contruire la suite définie par
, et
contruire la suite définie par ![]() et
pour tout
et
pour tout
![]() :
:
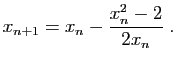
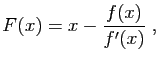 et
et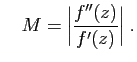
![]() , en partant de
, en partant de
![]() .
Voici les
.
Voici les ![]() premières valeurs de la suite
premières valeurs de la suite
![]() , à comparer
avec
, à comparer
avec
![]() .
.

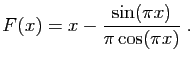
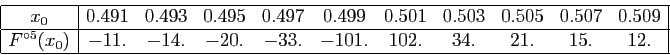
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales