Quand une série n'est pas à termes positifs, la première chose
à faire est d'examiner la série des valeurs absolues, ou des
modules s'il s'agit de nombres complexes.
Définition 3
On dit que la série  est absolument convergente si
la série
est absolument convergente si
la série
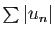 converge.
converge.
Théorème 8
Une série absolument convergente est convergente.
Démonstration : Supposons pour commencer que les 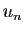 sont réels.
Pour tout
sont réels.
Pour tout
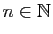 , notons
, notons
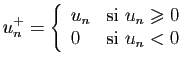
et
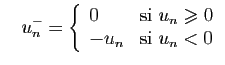
Pour tout
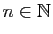 :
:
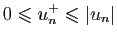
et
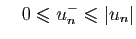
Par le théorème de comparaison, si
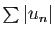 converge, alors
converge, alors
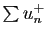 et
et
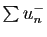 convergent. Par linéarité,
convergent. Par linéarité,
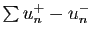 converge, or
converge, or
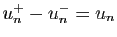 . D'où le résultat.
Passons maintenant au cas où les
. D'où le résultat.
Passons maintenant au cas où les 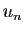 sont complexes. Notons
sont complexes. Notons 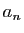 la partie réelle de
la partie réelle de 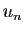 et
et 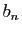 sa partie imaginaire. Pour tout
sa partie imaginaire. Pour tout
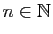 :
:
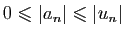
et
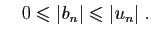
Par le théorème de comparaison, si
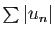 converge, alors
converge, alors
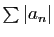 et
et
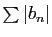 convergent aussi. Donc
convergent aussi. Donc 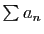 et
et 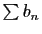 convergent, en appliquant le cas des séries à termes
réels.
Donc
convergent, en appliquant le cas des séries à termes
réels.
Donc  converge (proposition 1).
converge (proposition 1). Par exemple, pour tout
Par exemple, pour tout 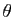 , la série
, la série
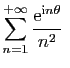
est absolument convergente.
En effet,
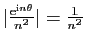 et
et
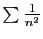 converge.
converge.
Comme autre exemple, pour tout complexe 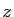 , la série exponentielle
, la série exponentielle
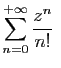
est absolument convergente,
car
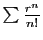 converge pour tout réel positif
converge pour tout réel positif 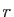 (application du critère de d'Alembert).
Il existe des séries convergentes, mais
qui ne sont pas absolument convergentes. Considérons par exemple
(application du critère de d'Alembert).
Il existe des séries convergentes, mais
qui ne sont pas absolument convergentes. Considérons par exemple
Les termes successifs s'annulent deux à deux, de sorte que les
sommes partielles valent
La suite des sommes partielles tend vers 0. Par contre la suite des
sommes partielles de
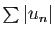 tend vers
tend vers 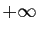 , par comparaison
avec la série de Riemann
, par comparaison
avec la série de Riemann
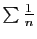 . Pour traiter ce type de
cas, on dispose du théorème suivant, dit théorème d'Abel
(un résultat analogue existe pour les intégrales).
. Pour traiter ce type de
cas, on dispose du théorème suivant, dit théorème d'Abel
(un résultat analogue existe pour les intégrales).
Démonstration : L'idée de la démontration est d'effectuer un changement dans la
sommation, qui s'apparente à une intégration par parties. Pour
tout
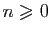 , posons
, posons
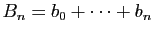 . Par hypothèse, la suite
. Par hypothèse, la suite
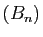 est bornée. Nous écrivons les sommes partielles de la
série
est bornée. Nous écrivons les sommes partielles de la
série
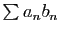 sous la forme suivante.
sous la forme suivante.
Comme 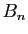 est borné, et
est borné, et 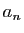 tend vers 0, le terme
tend vers 0, le terme 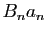 tend vers 0. Nous allons montrer que la série
tend vers 0. Nous allons montrer que la série
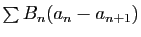 est absolument convergente. En effet,
est absolument convergente. En effet,
car la suite 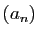 est une suite de réels positifs,
décroissante, et
est une suite de réels positifs,
décroissante, et 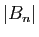 est borné par
est borné par 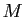 . Or :
. Or :
qui tend vers 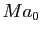 puisque
puisque 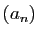 tend vers 0.
La série
tend vers 0.
La série
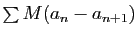 converge, donc la série
converge, donc la série
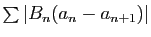 aussi, par le théorème de comparaison
3. Donc la série
aussi, par le théorème de comparaison
3. Donc la série
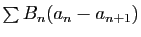 est convergente, donc la suite
est convergente, donc la suite 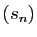 est convergente.
est convergente. Le cas d'application le plus fréquent est celui où
Le cas d'application le plus fréquent est celui où
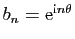 .
.
Corollaire 3
Soit 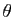 un réel tel que
un réel tel que
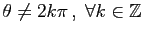 . Soit
. Soit 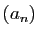 une suite de réels positifs, décroissante,
tendant vers 0 à l'infini. Les séries
une suite de réels positifs, décroissante,
tendant vers 0 à l'infini. Les séries
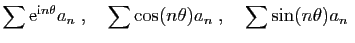
convergent.
Démonstration : Pour appliquer le théorème d'Abel 9 avec
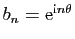 , nous devons
vérifier que les sommes partielles de la suite
, nous devons
vérifier que les sommes partielles de la suite
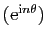 sont
bornées. Or
sont
bornées. Or
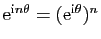 , et par hypothèse
, et par hypothèse
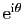 est différent de
est différent de 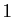 . On
a donc :
. On
a donc :
D'où le résultat. La convergence des séries
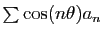 et
et
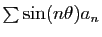 est une
conséquence directe de la proposition 1.
est une
conséquence directe de la proposition 1. Un cas particulier fréquemment rencontré est celui où
Un cas particulier fréquemment rencontré est celui où
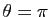 , soit
, soit
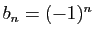 . On parle alors de série
alternée.
. On parle alors de série
alternée.
Terminons par une mise en garde : il n'est pas possible de remplacer
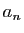 par un équivalent à l'infini dans le théorème
9, car la décroissance n'est pas conservée par
équivalence. Voici par exemple deux séries alternées.
par un équivalent à l'infini dans le théorème
9, car la décroissance n'est pas conservée par
équivalence. Voici par exemple deux séries alternées.
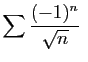
converge,
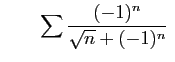
diverge.
Le théorème 9 s'applique a la première, mais
pas à la seconde, car si la suite
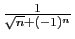 est
positive (pour
est
positive (pour
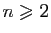 ), elle n'est pas
décroissante. Pourtant, on a bien :
), elle n'est pas
décroissante. Pourtant, on a bien :
Pour montrer que
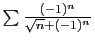 diverge,
calculons :
diverge,
calculons :
Ceci est le terme général d'une série à termes positifs
divergente (équivalente à la série de Riemann
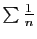 ). La différence de deux séries convergentes ne
peut pas être divergente. Or
). La différence de deux séries convergentes ne
peut pas être divergente. Or
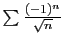 converge, donc
converge, donc
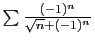 diverge.
diverge.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
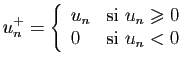 et
et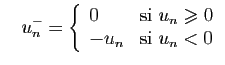
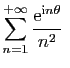 est absolument convergente.
est absolument convergente.
![]() , la série exponentielle
, la série exponentielle
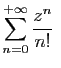 est absolument convergente,
est absolument convergente,
![\begin{displaymath}
u_n = \left\{
\begin{array}{ll}
\frac{1}{k+1}&\mbox{si } n=2k [2ex]
\frac{-1}{k+1}&\mbox{si } n=2k+1
\end{array}\right.
\end{displaymath}](img277.gif)
![\begin{displaymath}
s_n = \left\{
\begin{array}{cl}
\frac{1}{k+1}&\mbox{si } n=2k [2ex]
0&\mbox{si } n=2k+1
\end{array}\right.
\end{displaymath}](img278.gif)
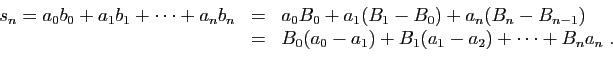
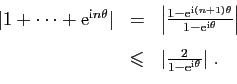
![]() par un équivalent à l'infini dans le théorème
9, car la décroissance n'est pas conservée par
équivalence. Voici par exemple deux séries alternées.
par un équivalent à l'infini dans le théorème
9, car la décroissance n'est pas conservée par
équivalence. Voici par exemple deux séries alternées.
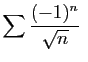 converge,
converge,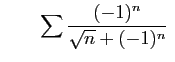 diverge.
diverge.
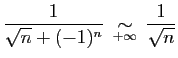
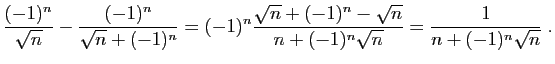
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales