Rappelons tout d'abord que la série géométrique 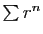 converge si
converge si 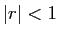 , diverge sinon. Les critères de Cauchy
et de d'Alembert permettent de comparer une série à termes
positifs avec les séries géométriques. Pour comparer
, diverge sinon. Les critères de Cauchy
et de d'Alembert permettent de comparer une série à termes
positifs avec les séries géométriques. Pour comparer 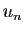 avec
avec
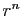 , le critère de Cauchy porte sur
, le critère de Cauchy porte sur
![$ \sqrt[n]{u_n}=(u_n)^{\frac{1}{n}}$](img198.gif) , le critère de d'Alembert
sur
, le critère de d'Alembert
sur
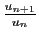 . Voici le premier.
. Voici le premier.
Démonstration : Rappelons que la nature de la série ne dépend pas de ses premiers
termes. Dans le premier cas,
Si 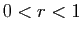 , alors la série
, alors la série 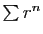 converge, d'où le résultat
par le théorème de comparaison 3.
converge, d'où le résultat
par le théorème de comparaison 3.
Dans le second cas,
Le terme général ne tend pas vers 0, donc la série diverge.  Comme exemple d'application, revenons sur les développements
décimaux. Étant donnée une suite
Comme exemple d'application, revenons sur les développements
décimaux. Étant donnée une suite 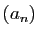 d'entiers tous compris
entre 0 et
d'entiers tous compris
entre 0 et
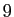 , la série
, la série
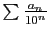 converge. En effet,
converge. En effet,
![$ \sqrt[n]{u_n}=\frac{1}{10}\sqrt[n]{a_n}$](img206.gif) . Or
. Or
![$ \sqrt[n]{a_n}\leqslant
\sqrt[n]{9}=\exp(\frac{1}{n}\ln(9))$](img207.gif) , qui tend vers
, qui tend vers 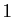 . Donc il existe
. Donc il existe
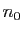 tel que pour
tel que pour 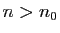 ,
,
![$ \sqrt[n]{u_n}<\frac{2}{10}$](img209.gif) , et la première
partie du critère s'applique. Observons que la suite
, et la première
partie du critère s'applique. Observons que la suite
![$ \sqrt[n]{u_n}$](img210.gif) ne converge pas, sauf si les
ne converge pas, sauf si les 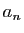 sont tous nuls ou
tous non nuls :
sont tous nuls ou
tous non nuls :
![$ \sqrt[n]{a_n}$](img211.gif) vaut 0
si
vaut 0
si 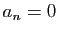 .
.
Dans les cas où la suite
![$ (\sqrt[n]{u_n})$](img213.gif) converge, la
position de sa limite par rapport à
converge, la
position de sa limite par rapport à 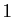 détermine
la nature de la série
détermine
la nature de la série  .
.
Corollaire 1
Soit  une série à termes positifs, telle que
une série à termes positifs, telle que
![$ \sqrt[n]{u_n}$](img210.gif) converge vers
converge vers 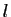 .
.
- Si
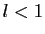 alors
alors  converge.
converge.
- Si
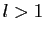 alors
alors  diverge.
diverge.
Si
![$ \sqrt[n]{u_n}$](img210.gif) tend vers
tend vers 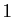 , on ne peut pas conclure en général.
Démonstration : Par définition de la limite, si
, on ne peut pas conclure en général.
Démonstration : Par définition de la limite, si 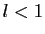 , alors il existe
, alors il existe 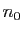 tel que
pour tout
tel que
pour tout 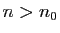 ,
,
et le premier cas du théorème 6 s'applique.
Si 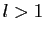 , alors il existe
, alors il existe 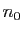 tel que
pour tout
tel que
pour tout 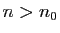 ,
,
et le second cas du théorème 6 s'applique. Par exemple,
Par exemple,
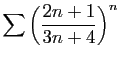
converge,
car
![$ \sqrt[n]{u_n}$](img210.gif) tend vers
tend vers
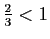 .
.
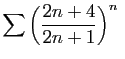
diverge,
car
![$ \sqrt[n]{u_n}>1$](img222.gif) .
.
Le critère de Cauchy ne s'applique ni aux séries de Riemann, ni
aux séries de Bertrand.
Or certaines de ces séries convergent, d'autres divergent.
Le critère de d'Alembert est plus facile à appliquer, par contre
il échoue plus souvent que celui de Cauchy.
Démonstration : Rappelons que la nature de la série ne dépend pas de ses premiers
termes. Dans le premier cas, on vérifie par récurrence que :
Si 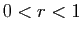 , alors la série
, alors la série 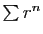 converge, d'où le résultat
par le théorème de comparaison 3.
converge, d'où le résultat
par le théorème de comparaison 3.
Si
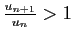 , la suite
, la suite 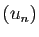 est croissante, elle ne
peut donc pas tendre vers 0 et la série diverge.
est croissante, elle ne
peut donc pas tendre vers 0 et la série diverge.  Observons que le théorème ne peut s'appliquer que si les
Observons que le théorème ne peut s'appliquer que si les 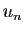 sont tous non nuls. En particulier, il ne s'applique pas aux
développements décimaux, contrairement au critère de Cauchy.
sont tous non nuls. En particulier, il ne s'applique pas aux
développements décimaux, contrairement au critère de Cauchy.
Définissons la suite 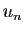 par :
par :
Le rapport
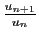 vaut
vaut
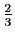 si
si 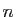 est pair,
est pair,
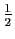 si
si 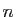 est impair. Il est donc toujours inférieur à
est impair. Il est donc toujours inférieur à
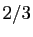 , et la série converge.
, et la série converge.
Définissons maintenant :
Le rapport
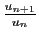 vaut
vaut
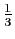 si
si 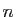 est pair,
est pair,
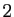 si
si 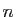 est impair. Le critère de d'Alembert ne s'applique
pas. Pourtant,
est impair. Le critère de d'Alembert ne s'applique
pas. Pourtant,
![$ \sqrt[n]{u_n}$](img210.gif) converge vers
converge vers
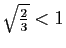 ,
donc le critère de Cauchy s'applique (la série converge).
,
donc le critère de Cauchy s'applique (la série converge).
Ici encore, quand la suite
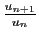 converge, la position
de la limite par rapport à
converge, la position
de la limite par rapport à 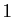 détermine la nature de la série.
détermine la nature de la série.
Corollaire 2
Soit  une série à termes positifs, telle que
une série à termes positifs, telle que
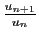 converge vers
converge vers 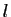 .
.
- Si
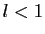 alors
alors  converge.
converge.
- Si
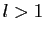 alors
alors  diverge.
diverge.
Si
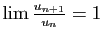 , on ne peut pas conclure en général.
Démonstration : Par définition de la limite, si
, on ne peut pas conclure en général.
Démonstration : Par définition de la limite, si 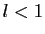 , alors il existe
, alors il existe 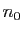 tel que
pour tout
tel que
pour tout 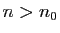 ,
,
et le premier cas du théorème 7 s'applique.
Si 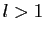 , alors il existe
, alors il existe 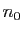 tel que
pour tout
tel que
pour tout 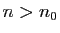 ,
,
et le second cas du théorème 7 s'applique. Par exemple, pour tout réel positif
Par exemple, pour tout réel positif 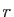 , la série exponentielle
, la série exponentielle
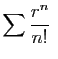
converge.
car
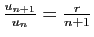 tend vers
tend vers 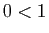 . (On pourrait
aussi appliquer le critère de Cauchy, mais c'est moins facile.)
. (On pourrait
aussi appliquer le critère de Cauchy, mais c'est moins facile.)
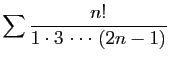
converge,
car
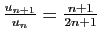 tend vers
tend vers
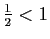 .
.
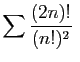
diverge,
car
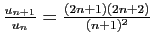 tend vers
tend vers  .
.
Le critère de d'Alembert ne s'applique ni aux séries de Riemann, ni
aux séries de Bertrand.
Plus généralement, si 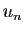 est une fraction rationnelle en
est une fraction rationnelle en  et
et
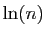 , alors les deux critères échouent. Dans ce cas, il faut
calculer un équivalent et appliquer le
théorème 4.
, alors les deux critères échouent. Dans ce cas, il faut
calculer un équivalent et appliquer le
théorème 4.
Nous avons vu un exemple pour lequel seul le critère de Cauchy
donnait la réponse. Il est en effet plus puissant, comme le montre
la proposition suivante.
Démonstration : Pour tout
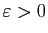 , il existe
, il existe 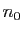 tel que pour tout
tel que pour tout
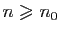 ,
,
Par récurrence, on en déduit :
or :
![$\displaystyle \lim_{n\rightarrow\infty}\sqrt[n]{u_{n_0}(l-\varepsilon)^{n-n_0}}
= l-\varepsilon$](img254.gif)
et
![$\displaystyle \quad
\lim_{n\rightarrow\infty}\sqrt[n]{u_{n_0}(l+\varepsilon)^{n-n_0}}
= l+\varepsilon\;.
$](img255.gif)
Donc il existe 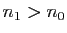 tel que pour
tel que pour 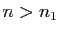 ,
,
d'où le résultat.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() converge, la
position de sa limite par rapport à
converge, la
position de sa limite par rapport à ![]() détermine
la nature de la série
détermine
la nature de la série ![]() .
.
![$\displaystyle \sqrt[n]{u_n}<l+\frac{1-l}{2}=\frac{l+1}{2}<1\;,
$](img217.gif)
![]() , alors il existe
, alors il existe ![]() tel que
pour tout
tel que
pour tout ![]() ,
,
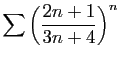 converge,
converge,
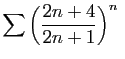 diverge,
diverge,
![$\displaystyle \lim_{n\rightarrow\infty} \sqrt[n]{n^{-\alpha}}=
\lim_{n\rightarrow\infty} \sqrt[n]{n^{-1}(\ln(n))^{-\beta}}=1\;.
$](img223.gif)
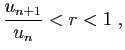 alors
alors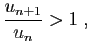 alors
alors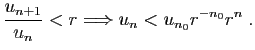
![]() , la suite
, la suite ![]() est croissante, elle ne
peut donc pas tendre vers 0 et la série diverge.
est croissante, elle ne
peut donc pas tendre vers 0 et la série diverge. ![]() Observons que le théorème ne peut s'appliquer que si les
Observons que le théorème ne peut s'appliquer que si les ![]() sont tous non nuls. En particulier, il ne s'applique pas aux
développements décimaux, contrairement au critère de Cauchy.
sont tous non nuls. En particulier, il ne s'applique pas aux
développements décimaux, contrairement au critère de Cauchy.
![]() par :
par :
![\begin{displaymath}
u_n = \left\{
\begin{array}{ll}
\frac{1}{3^k}&\mbox{si } n=2k [2ex]
\frac{2}{3^{k+1}}&\mbox{si } n=2k+1
\end{array}\right.
\end{displaymath}](img228.gif)
![\begin{displaymath}
u_n = \left\{
\begin{array}{ll}
\frac{2^k}{3^k}&\mbox{si } n...
...[2ex]
\frac{2^k}{3^{k+1}}&\mbox{si } n=2k+1
\end{array}\right.
\end{displaymath}](img232.gif)
![]() converge, la position
de la limite par rapport à
converge, la position
de la limite par rapport à ![]() détermine la nature de la série.
détermine la nature de la série.
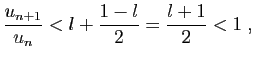
![]() , alors il existe
, alors il existe ![]() tel que
pour tout
tel que
pour tout ![]() ,
,
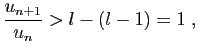
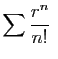 converge.
converge.
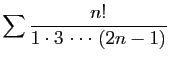 converge,
converge,
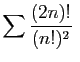 diverge,
diverge,
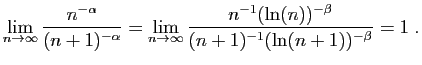
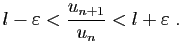
![$\displaystyle \lim_{n\rightarrow\infty}\sqrt[n]{u_{n_0}(l-\varepsilon)^{n-n_0}}
= l-\varepsilon$](img254.gif) et
et![$\displaystyle \quad
\lim_{n\rightarrow\infty}\sqrt[n]{u_{n_0}(l+\varepsilon)^{n-n_0}}
= l+\varepsilon\;.
$](img255.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales