Les séries à termes positifs ou nuls
sont plus faciles à étudier. En effet si
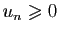 pour
tout
pour
tout 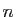 , la suite des sommes partielles est croissante.
, la suite des sommes partielles est croissante.
Une suite croissante
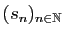 n'a que deux comportements
possibles. Soit elle est majorée
et elle converge, soit elle tend vers
n'a que deux comportements
possibles. Soit elle est majorée
et elle converge, soit elle tend vers 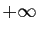 .
.
Les séries à termes positifs se comparent comme les intégrales
de fonctions positives.
Théorème 3
Soient  et
et 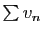 deux séries à termes positifs ou nuls. On
suppose qu'il existe
deux séries à termes positifs ou nuls. On
suppose qu'il existe
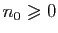 tel que pour tout
tel que pour tout
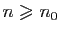 ,
,
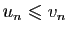 .
.
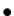
- Si
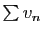 converge alors
converge alors  converge.
converge.
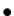
- Si
 diverge alors
diverge alors 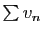 diverge.
diverge.
Démonstration : Comme nous l'avons observé, la convergence ne dépend pas des
premiers termes. On peut donc étudier les sommes partielles à
partir de 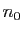 . Pour tout
. Pour tout
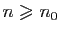 , notons
, notons
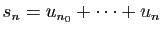 et
et
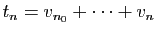 . Les suites
. Les suites
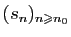 et
et
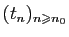 sont croissantes, et de plus pour tout
sont croissantes, et de plus pour tout
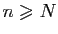
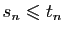 . Si la série
. Si la série 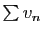 converge, alors la suite
converge, alors la suite
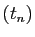 converge. Soit
converge. Soit 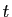 sa limite. La suite
sa limite. La suite 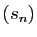 est croissante,
et majorée par
est croissante,
et majorée par 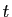 , donc elle converge, donc la série
, donc elle converge, donc la série  converge aussi. Inversement, si la série
converge aussi. Inversement, si la série  diverge, alors
la suite
diverge, alors
la suite 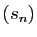 tend vers
tend vers 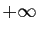 , et il en est de même pour la
suite
, et il en est de même pour la
suite 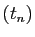 .
.  Comme premier exemple, considérons un développement décimal. Soit
Comme premier exemple, considérons un développement décimal. Soit
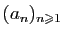 une suite d'entiers tous compris entre 0 et
une suite d'entiers tous compris entre 0 et 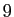 . La série
. La série
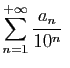
converge.
En effet, son terme général
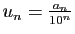 est majoré par
est majoré par
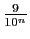 . La série géométrique
. La série géométrique
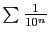 converge, car
converge, car
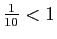 . La série
. La série
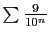 converge aussi par linéarité, d'où le résultat.
Nous avons déjà vu que la
série
converge aussi par linéarité, d'où le résultat.
Nous avons déjà vu que la
série
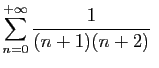
converge.
Nous allons en déduire que
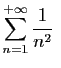
converge.
En effet :
En particulier, il existe 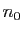 tel que pour
tel que pour
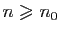 :
:
En fait c'est vrai pour
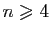 , mais il est inutile de calculer une
valeur précise de
, mais il est inutile de calculer une
valeur précise de 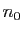 . On en déduit que la série de terme
général
. On en déduit que la série de terme
général
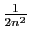 converge, d'où le résultat par
linéarité. Montrons maintenant que
converge, d'où le résultat par
linéarité. Montrons maintenant que
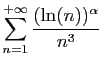
converge,
pour tout réel 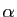 . En effet :
. En effet :
Donc il existe 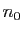 tel que pour
tel que pour
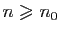 ,
,
En multipliant les deux membres par
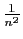 :
:
Comme la série
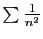 converge, il en est de même de
la série
converge, il en est de même de
la série
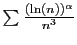 , par le théorème
3.
, par le théorème
3.
Inversement, nous avons vu que la série
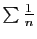 diverge. On en déduit facilement que les séries
diverge. On en déduit facilement que les séries
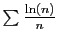 et
et
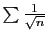 divergent également.
Le théorème de comparaison permet
d'utiliser des équivalents.
divergent également.
Le théorème de comparaison permet
d'utiliser des équivalents.
Démonstration : Par hypothèse, pour tout
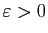 , il existe
, il existe 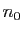 tel que pour
tout
tel que pour
tout
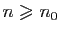 ,
,
Fixons
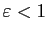 .
Si
.
Si  converge, alors par le théorème de comparaison
3,
converge, alors par le théorème de comparaison
3,
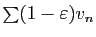 converge, donc
converge, donc
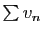 également. Réciproquement, si
également. Réciproquement, si  diverge, alors
diverge, alors
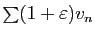 diverge, et
diverge, et 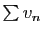 aussi.
aussi. Par exemple,
Par exemple,
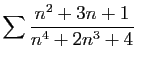
converge,
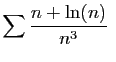
converge.
Dans les deux cas, le terme général est équivalent à
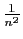 , et nous avons vu que la série
, et nous avons vu que la série
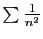 converge. Par contre
converge. Par contre
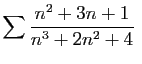
diverge,
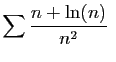
diverge.
Dans les deux cas, le terme général est équivalent à
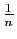 , et nous avons vu que la série
, et nous avons vu que la série
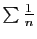 diverge.
diverge.
Les théorèmes 3 et
4 permettent de ramener les séries à
termes positifs à un catalogue de séries dont la convergence est
connue. Dans ce catalogue, on trouve les séries de Riemann
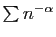 et de
Bertrand
et de
Bertrand
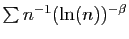 .
On les étudie en utilisant les intégrales
correspondantes grâce au théorème suivant, illustré sur la
figure 2.
.
On les étudie en utilisant les intégrales
correspondantes grâce au théorème suivant, illustré sur la
figure 2.
Figure 2:
Comparaison entre une série à termes positifs et
l'intégrale d'une fonction décroissante sur
 .
.
|
|
Théorème 5
Soit 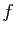 une fonction de
une fonction de
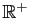 dans
dans
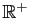 , décroissante.
La série de terme général
, décroissante.
La série de terme général 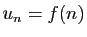 est de même nature
(convergente ou divergente) que l'intégrale
est de même nature
(convergente ou divergente) que l'intégrale
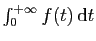 .
.
Démonstration : Comme 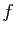 est décroissante, les inégalités
est décroissante, les inégalités
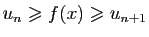 sont vraies pour tout
sont vraies pour tout
![$ x\in[n,n+1]$](img155.gif) . En intégrant entre
. En intégrant entre 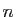 et
et 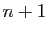 on obtient :
on obtient :
Par la relation de Chasles, la somme de 0 à 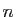 donne :
donne :
La série  converge et a pour somme
converge et a pour somme 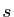 ,
si et seulement si la suite des sommes
partielles converge vers
,
si et seulement si la suite des sommes
partielles converge vers 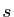 .
Dans ce cas
.
Dans ce cas
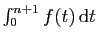 est
majorée par
est
majorée par 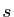 , et comme
, et comme
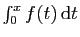 est fonction croissante de
est fonction croissante de
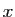 , l'intégrale converge. Réciproquement, si l'intégrale
converge, alors
, l'intégrale converge. Réciproquement, si l'intégrale
converge, alors
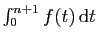 est majorée, la suite des
sommes partielles aussi, et elle converge.
est majorée, la suite des
sommes partielles aussi, et elle converge. Rappelons que le point de départ de la sommation n'a pas d'influence
sur la convergence des séries. Le théorème
5 reste vrai pour des fonctions définies sur
Rappelons que le point de départ de la sommation n'a pas d'influence
sur la convergence des séries. Le théorème
5 reste vrai pour des fonctions définies sur
 au lieu de
au lieu de
 . Nous l'appliquons à
. Nous l'appliquons à
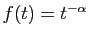 , puis
, puis
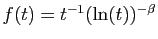 .
.
Séries de Riemann
Si
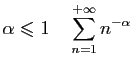
diverge.
Si
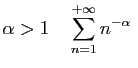
converge.
Si
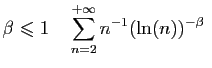
diverge.
Si
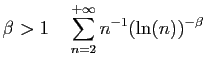
converge.
Nous retrouvons en particulier le fait que
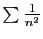 converge,
alors que
converge,
alors que
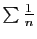 diverge. Voici deux exemples
d'utilisation des équivalents pour la comparaison avec les
séries de Riemann et de Bertrand.
diverge. Voici deux exemples
d'utilisation des équivalents pour la comparaison avec les
séries de Riemann et de Bertrand.
La série
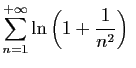
converge.
En effet :
et la série de Riemann
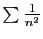 converge.
converge.
La série
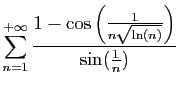
diverge.
En effet :
et la série de Bertrand
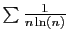 diverge.
Nous allons à nouveau appliquer le théorème de comparaison,
pour montrer que si le terme général d'une série est un
produit de facteurs dont l'un est dominant, alors la nature de la
série est dictée par le terme dominant.
diverge.
Nous allons à nouveau appliquer le théorème de comparaison,
pour montrer que si le terme général d'une série est un
produit de facteurs dont l'un est dominant, alors la nature de la
série est dictée par le terme dominant.
Démonstration : Par hypothèse, il existe 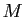 tel que :
tel que :
En multipliant les deux membres par 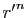 , on obtient :
, on obtient :
D'où le résultat par le théorème de comparaison
3, puisque
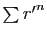 converge.
converge. Comme application de cette proposition, si
Comme application de cette proposition, si 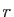 est tel que
est tel que 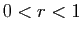 et
et
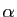 est un réel quelconque, la série
est un réel quelconque, la série
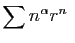
converge.
Démonstration : Par hypothèse, il existe 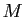 tel que :
tel que :
En multipliant les deux membres par
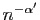 , on obtient :
, on obtient :
D'où le résultat par le théorème de comparaison
3, puisque
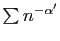 converge.
converge. Comme conséquence de cette proposition, pour tout
Comme conséquence de cette proposition, pour tout 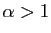 et pour
tout réel
et pour
tout réel 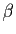 ,
,
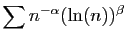
converge.
Dans le catalogue des séries dont la nature est connue,
on trouve aussi les séries géométriques et la série
exponentielle. Pour la comparaison avec les séries
géométriques, il existe deux critères mieux adaptés que les
équivalents. Ils font l'objet de la section suivante.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
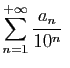 converge.
converge.
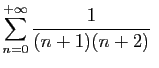 converge.
converge.
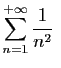 converge.
converge.
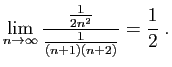
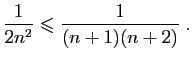
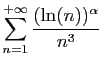 converge,
converge,
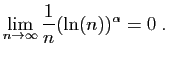
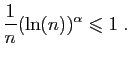
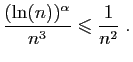
![]() diverge. On en déduit facilement que les séries
diverge. On en déduit facilement que les séries
![]() et
et
![]() divergent également.
Le théorème de comparaison permet
d'utiliser des équivalents.
divergent également.
Le théorème de comparaison permet
d'utiliser des équivalents.
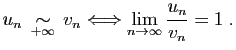
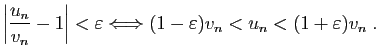
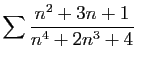 converge,
converge,
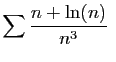 converge.
converge.
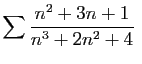 diverge,
diverge,
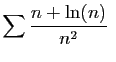 diverge.
diverge.
![]() et de
Bertrand
et de
Bertrand
![]() .
On les étudie en utilisant les intégrales
correspondantes grâce au théorème suivant, illustré sur la
figure 2.
.
On les étudie en utilisant les intégrales
correspondantes grâce au théorème suivant, illustré sur la
figure 2.
![\includegraphics[width=12cm]{serieintegrale2}](img151.gif)
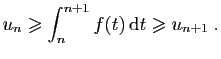
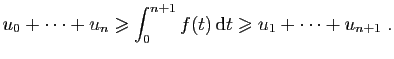
![$\displaystyle \int_1^{x} t^{-\alpha} \mathrm{d}t =
\left\{\begin{array}{ll}
\d...
...box{si }\alpha\neq
1 [1.5ex]
\ln(x) &\mbox{si }\alpha=1
\end{array}\right.
$](img164.gif)
![$\displaystyle \int_2^{x} t^{-1}(\ln(t))^{-\beta} \mathrm{d}t =
\left\{\begin{a...
...eq
1 [1.5ex]
\ln(\ln(x))-\ln(\ln(2)) &\mbox{si }\beta=1
\end{array}\right.
$](img165.gif)
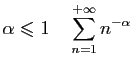 diverge.
diverge.
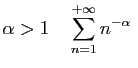 converge.
converge.
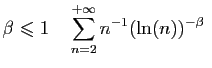 diverge.
diverge.
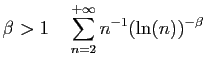 converge.
converge.
![]() converge,
alors que
converge,
alors que
![]() diverge. Voici deux exemples
d'utilisation des équivalents pour la comparaison avec les
séries de Riemann et de Bertrand.
diverge. Voici deux exemples
d'utilisation des équivalents pour la comparaison avec les
séries de Riemann et de Bertrand.
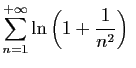 converge.
converge.
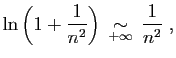
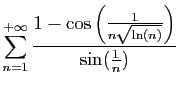 diverge.
diverge.
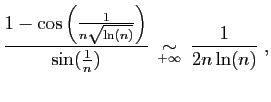
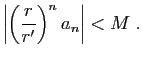
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales